In this part of Evolution 101 series, I will introduce you to the "language" of population genetics and explain the basic population genetics model describing genotypes and allele frequencies in population.
Genotype, phenotype, genes, alleles
I'm sure that most of you have heard about those terms from the heading, but never really understood them, right?
Well, population genetics is not scary and difficult to understand as you may think! So let's start with the basics.
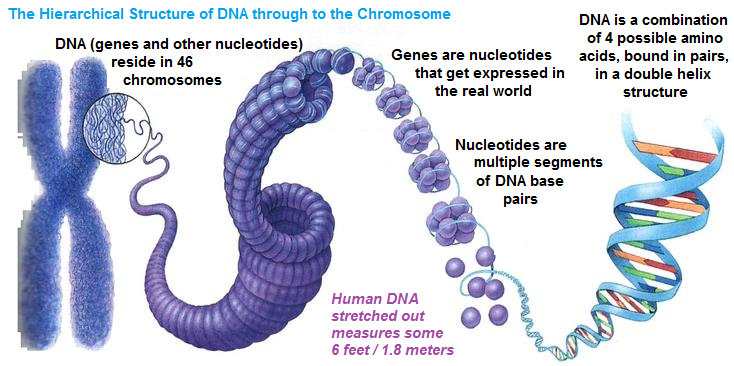
Chromosomes, DNA, genes, nucleotides
Source
Each of our cells (except mature red blood cells and dead cells in hair, skin and nails) contains 46 chromosomes which represent densely packed DNA, carrier of our genetic information.
DNA consists of building blocks - nucleotides (A, T, G, C, precisely 3 billion of these in pairs in our whole genome!), which are arranged in certain manner, forming sequences with specific functions, like genes.
According to general definition, genes are basic physical and functional units of heredity which means that they provide instructions for protein synthesis. The human genome consists of about 20 000 protein-coding genes.
Alleles are different forms of the SAME gene, meaning that they slightly differ among themselves in their nucleotide sequences.

Gene coding for eye color can exist in different allele forms - brown, blue, green, etc.
Source
Genotype is complete heritable genetic information carried by the individual. However, it can also refer to set of genes which is responsible for development of certain characteristics.
Phenotype is basically everything you can observe in one organism - all morphological, physiological, biochemical and behavioral traits, and represents observable "consequence" of genotype expression.
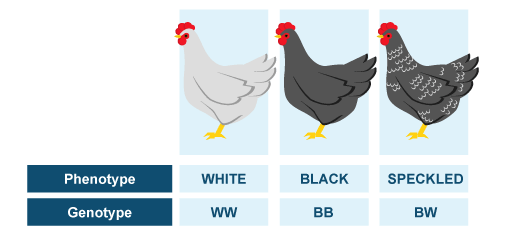
Difference between genotype and phenotype
Source
Population genetics - genotype and allele frequencies
I have already mentioned that human genome contains about 20 000 genes loci.
The simplest case which is often used to explain genotype and allele frequencies is example with one genetic locus which has two alleles (A and a) and consequently, there would be three possible genotypes within population (AA, Aa, and aa).
Frequencies of these genotypes can be expressed in following manner:
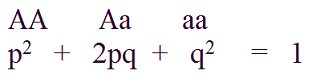
The sum of frequencies of all individual genotypes must be equal to 1 (or 100%).
For example, let's imagine population of 10 individuals, with genotypes:
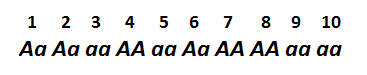
We can easily calculate genotype frequencies in this population:
Frequency of AA = 3/10 = 0.3 (or 30%)
Frequency of Aa = 3/10 = 0.3 (or 30%)
Frequency of aa = 4/10 = 0.4 (or 40%)
So genotype frequencies are calculated simply by counting the number of each genotype and diving it by the total number of organisms in population.
Likewise, allele frequencies are calculated by counting how many times each of the alleles appear in a population, and dividing that number with total number of alleles for that gene locus in population:
Frequency of A = 9/20 = 0.45
Frequency of a = 11/20 = 0.55
So in our imaginary population, allele A appears 9 times and allele a 11 times, in a population which has total number of 20 alleles for this gene locus.
Hardy–Weinberg principle and genetic equilibrium
The main question in population genetics is - if we know the genotype (and allele) frequencies in one generation, how can we predict those frequencies in the next generation?
To be able to make such assumptions, population geneticists need to use certain type of population model. This model assumes existence of "perfect populations", which of course do not exist in real life.
This is called Hardy–Weinberg principle and includes following assumptions:
- Hypothetical population is infinitely large
- Individuals of such population mate among themselves randomly (no mating preferences)
- Sex ratio is 1:1
- There are no overlapping generations
- There are no evolutionary mechanisms that could change the allele frequencies (no natural selection, no mutations, no migrations, etc.)

In Hardy–Weinberg "perfect" populations, there are no changes in allele frequencies throughout generations
Source
In such hypothetical population, genetic or Hardy–Weinberg equilibrium is achieved - allele frequencies stay the same throughout generations and genotype frequencies can be determined from allele frequencies.
What are the implications of hypothetical random mating? This implicates that after one generation of random mating, the Hardy–Weinberg genotype frequencies are reached regardless the initial genotype frequencies, and the population will stay in Hardy–Weinberg equilibrium as long as mating is random, the population size is large and there are no evolution mechanisms working to change allele frequencies.
In this state, we can easily calculate genotype frequencies from allele frequencies, by using already familiar equation:
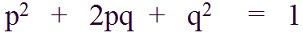
Why is Hardy–Weinberg theorem important?
Although Hardy–Weinberg theorem can have prediction significance in some rare cases (MN blood group genotype frequencies in three American populations are very close to Hardy–Weinberg equilibrium), we cannot expect that real populations behave according to Hardy–Weinberg principle.
However, it represents a good starting point for investigation of real populations genotype frequencies. By comparison of real populations with Hardy–Weinberg ratios, we can observe in what level those real populations we're interested in deviate from the hypothetical population in equilibrium, and what evolution mechanisms are responsible for that deviation.
In the next post, we will start discussing about different mechanisms of evolution and in what way they change allele frequencies in population.
Until then, relax and keep steemSTEM! ;)
Literature
Evolution, Mark Ridley, 3rd Edition
For more scientific-related content check steemSTEM. Follow me if you like my posts and want to read some more ;) If you have any thoughts/suggestions fell free to leave a comment!

