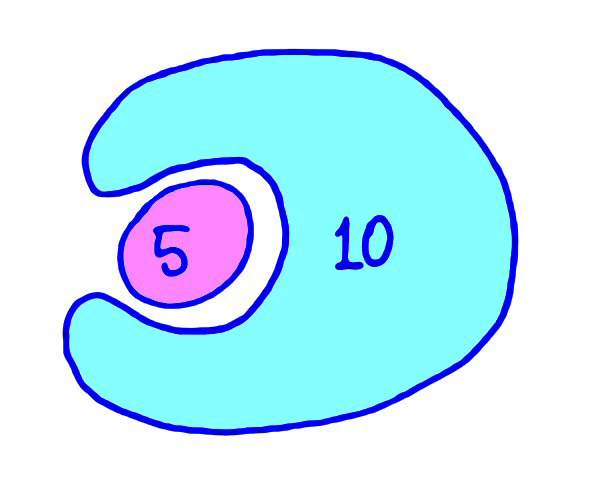
Can a number eat and swallow another number?
Before we examine this proposition, look at the problem below.

There are many ways to find the Lowest Common Multiple (LCM) of numbers. In this article, I introduce a new and fun way to do it.
Those of you who have played agar.io would know that it is an addictive computer game. You start as a small circle and you eat other circles and grow. Sometimes, to as a defence mechanism, you may split your circle into smaller circles.
You can also do this sort of absorption and splitting to find the Lowest Common Multiple (LCM) of numbers.
Here are the rules:-
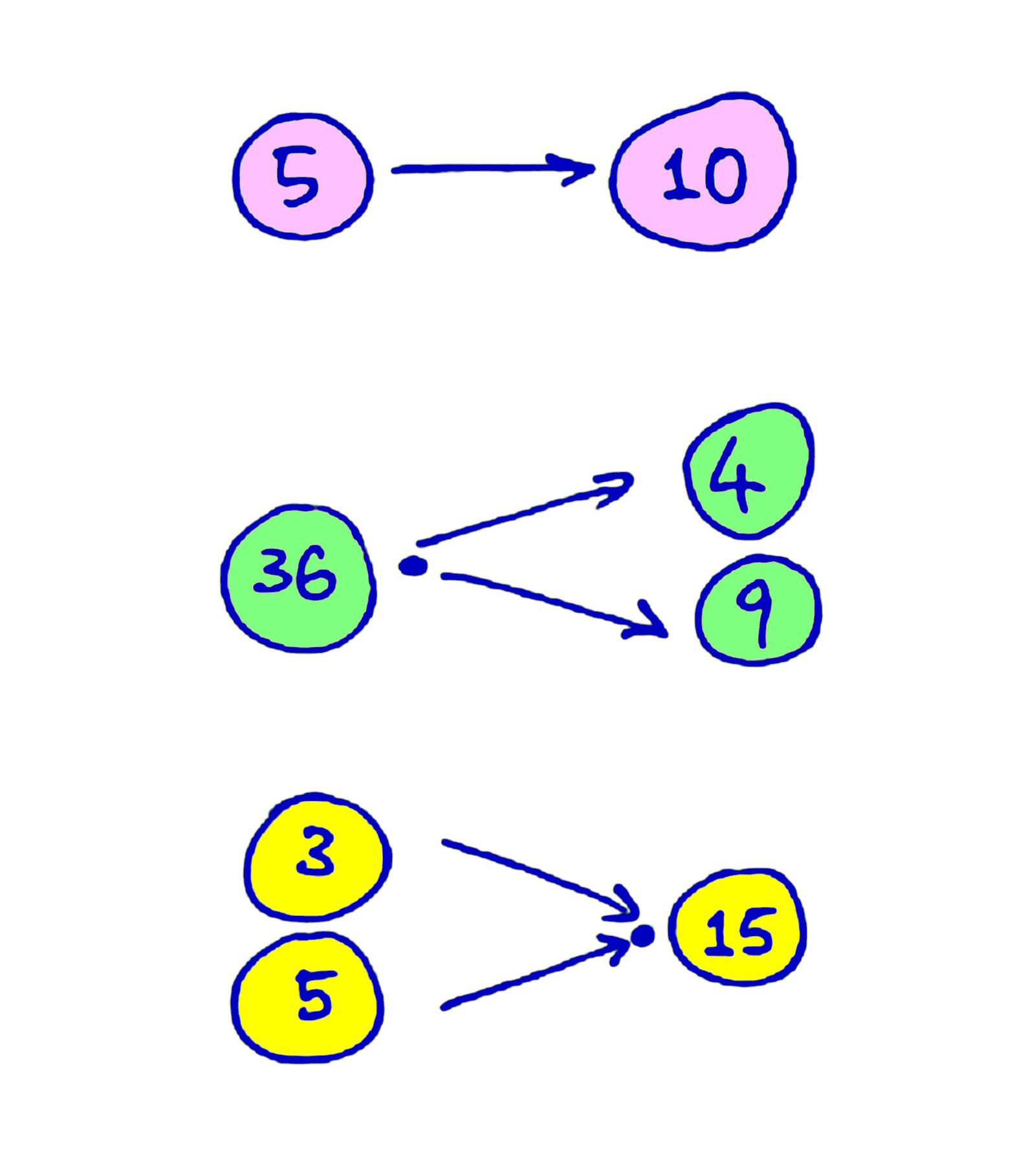
Rule #1 : If a number is a factor of another number, it gets absorbed by that number. So for example, 5 will get eaten up by 10 because 5 is a factor of 10. 10 can be divided by 5 cleanly with no remainder.
Rule #2 : A number can split into prime powers of distinct primes. For example, 36 splits into 4 and 9 (representing 4 × 9). 4 is a power of the prime number 2. 9 is a power of the prime number 3. 4 and 9, coming from different prime numbers, have no factor in common. Note, that you want to conserve the highest power (no pun intended), so for example you do not split the 4 further into 2 × 2.
Rule #3 : Different numbers with no factors in common can combine and they get multiplied together. For example, 3 and 5 have no factors in common, and they combine together as 15. You can combine more than 2 numbers by repeatedly applying this rule.
Let us study a few examples to see how these rules work.
Example 1
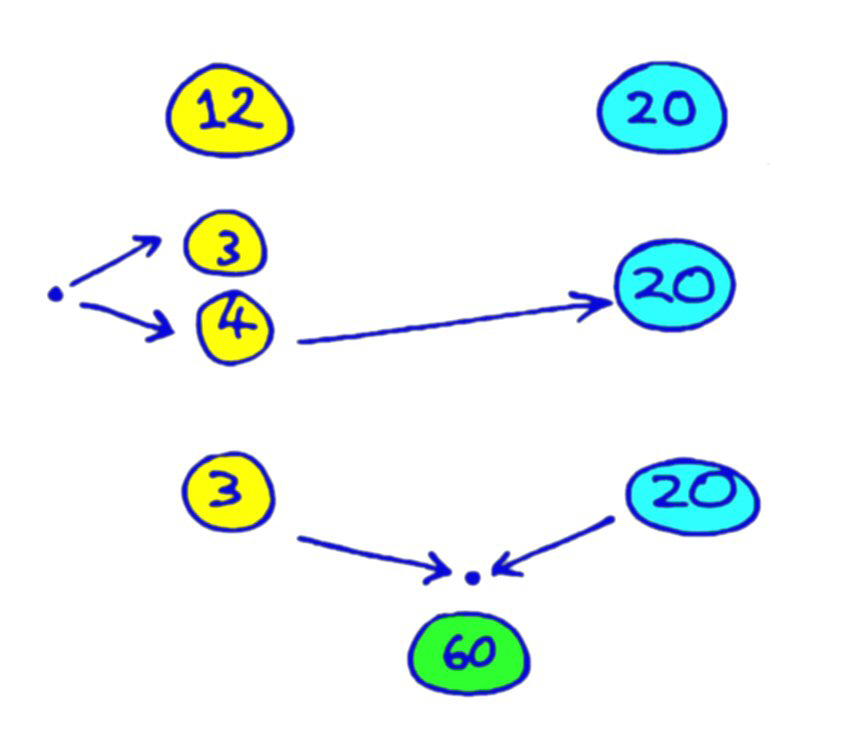
Let's say you want the LCM of 12 and 20. 12 splits as 3 × 4. (Rule #2) 4 gets eaten up by 20.(Rule #1) 3 and 20 are coprime, so they combine as 3 × 20 = 60.(Rule #3)
Example 2
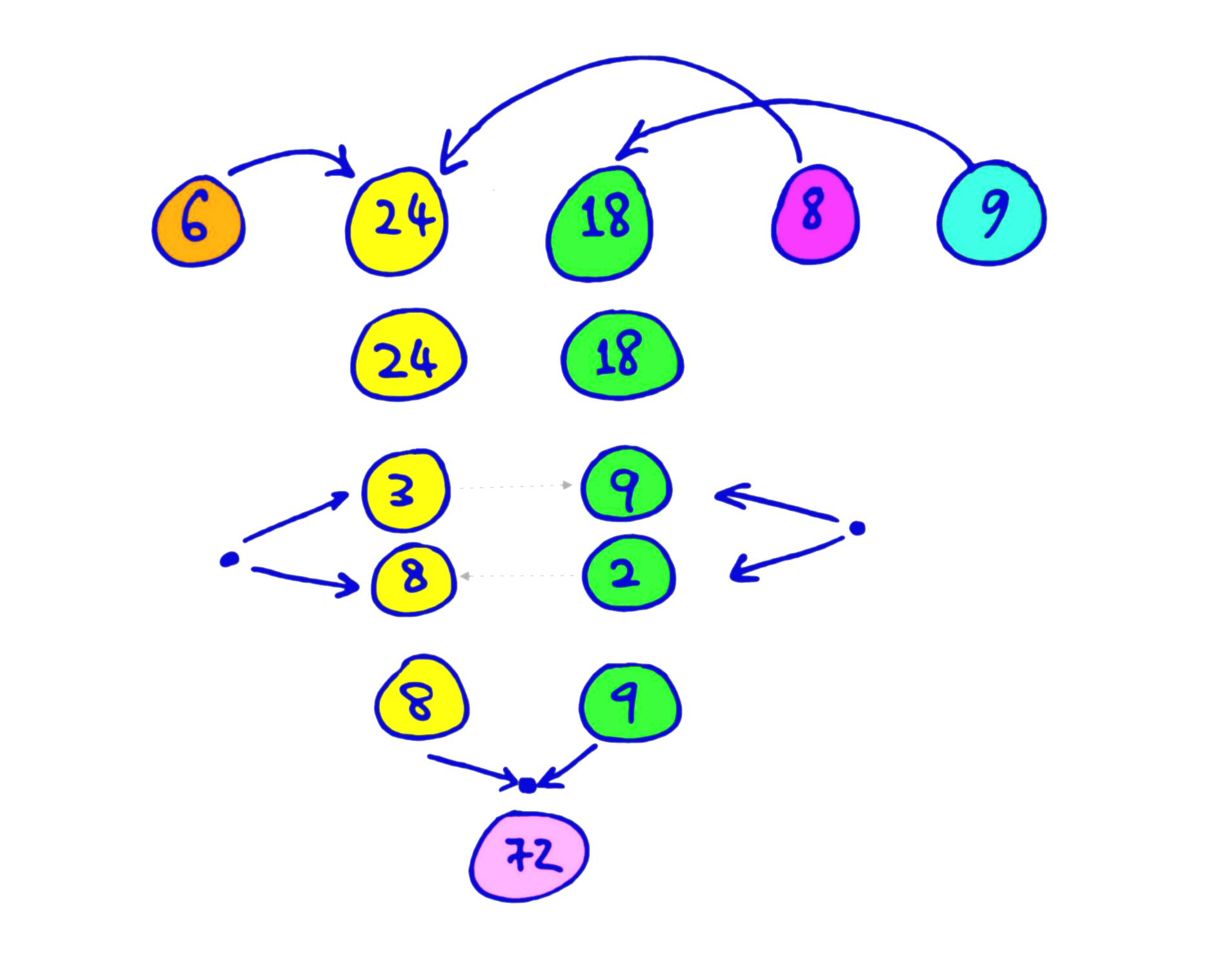
We have 5 numbers here. It looks more challenging. But immediately you see that 6 and 8 get eaten up by 24, and 9 gets absorbed into 18. (Rule #1) So now we have 24 and 18. 24 splits as 3 × 8, while 18 splits as 9 × 2. (Rule #2) Now 9 swallows up 3, while 2 gets eaten by 8. (Rule #1) So we have 8 and 9 which join to give 72. (Rule #3)
Example 3

By now, you should be able to visualise the absorption and splitting in your mind. In this example, 8 eats up 4, 7 gets eaten up by 14, and 6 gets absorbed by 18. 14 splits as 2 × 7, while 18 splits as 2 × 9. Then 8 eats away the two copies of 2. We are left with 8, 7 and 9, which combine to give 504.
Example 4
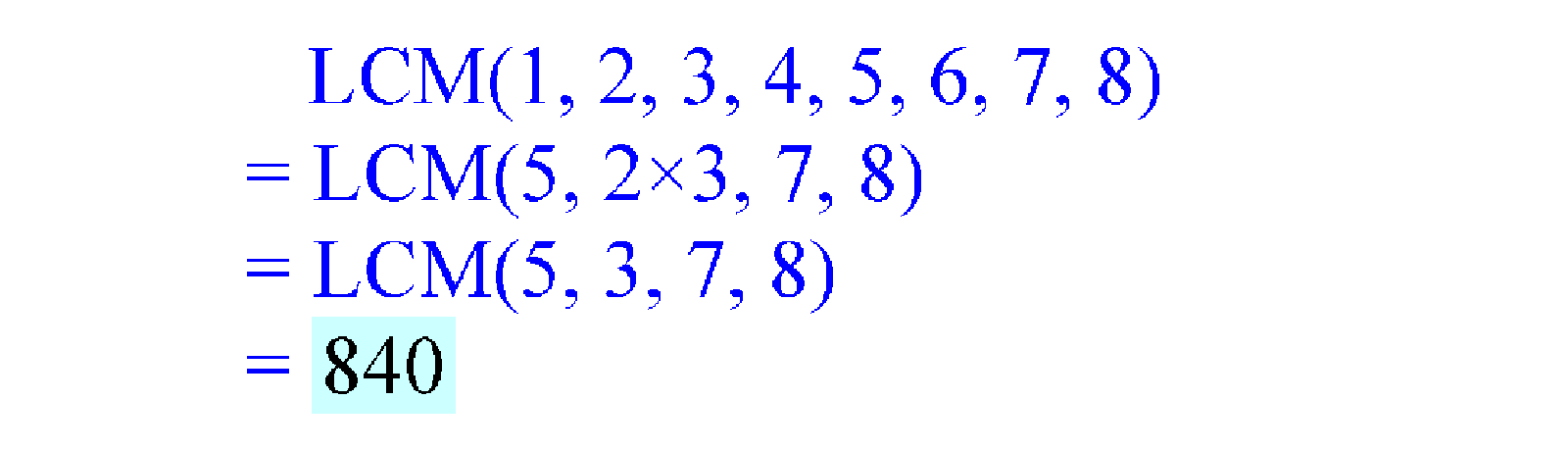
This is the problem posed in the beginning. It seems difficult, but once you know the rules, this is a piece of cake. To start off, 8 eats 4, 2 and 1. 6 swallows up 3. The 6 splits as 2 × 3. 8 then eats the 2. We are left with 5, 3, 7 and 8. These combine to give 840.
Voilà! Done!
This is fun, eh? Forrest Gump says "life is like a box of chocolates". I say:"Finding LCM is like playing agar.io"!
