Here is a confounding geometrical Mathematics problem around primary 5 or 6 (~ grade 5 or 6) level in Singapore. Take a look:-
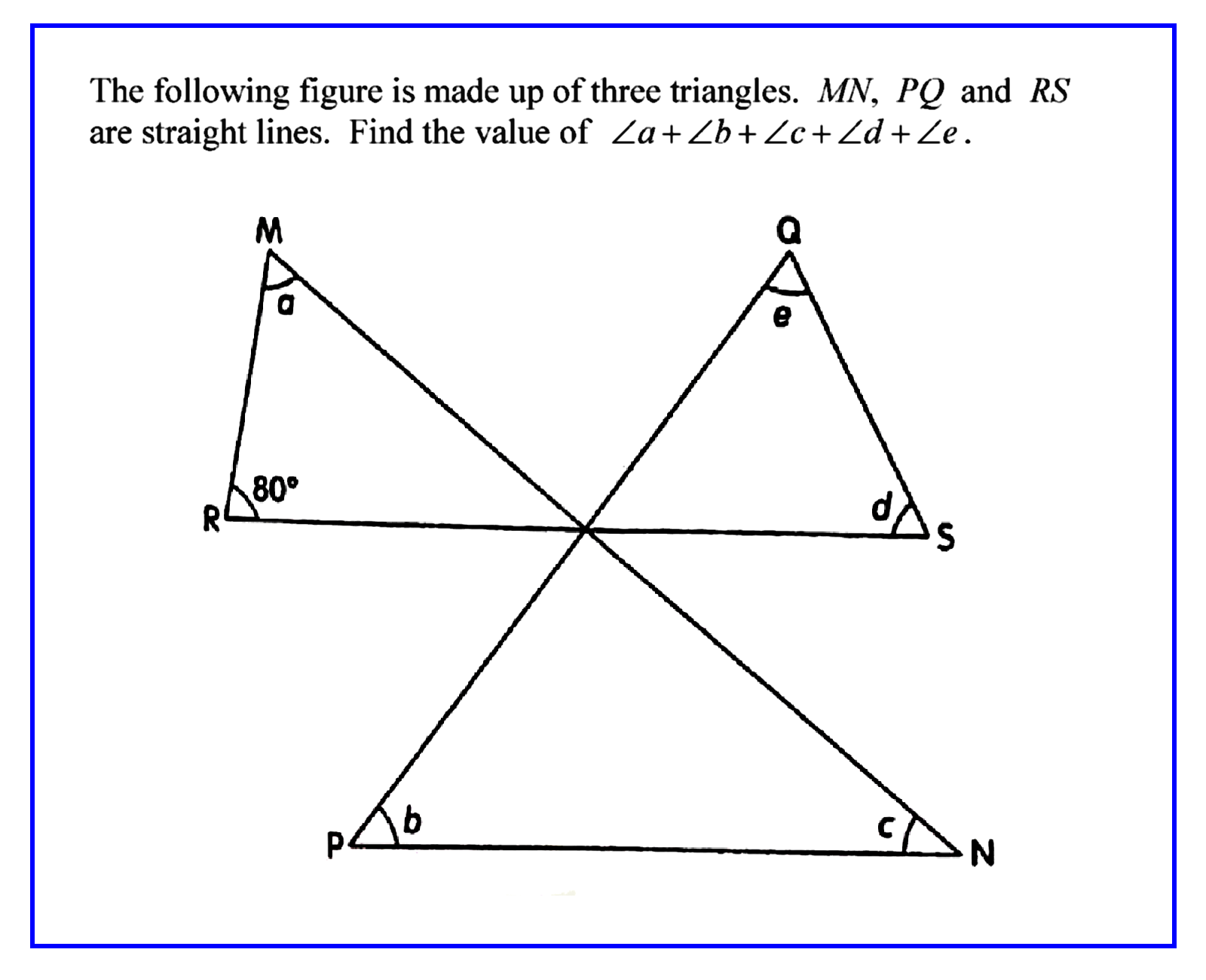
Have a go at it!
Hmmmmm ....
There are five unknowns, aren’t there?
It looks like we are only given one piece of numerical information viz. the 80° angle. So ...
How can we find the individual unknowns?
We do not even know (the measures of) those five angles, how can we hope to find their sum total?
Oh dear! This is sooooooooooo mind-boggling ...
Give up?
Why don't you give it ooooooooooooooone more try?
External Angle of a Triangle
Before I present my solution, it is useful to know that the external angle of a triangle is equal to the sum of the internal opposite angles. What does that mean? In the triangle below, the angle ABD is an external angle of the triangle ABC. Basically, CB is produced (extended) to the point A outside of the triangle. Imagine: if you are standing at the external angle ABD and you step into the triangle, you see the internal angles BDC = x and BCD = y opposite you. And the measurement of ABD will be the sum x + y of those two interior angles.
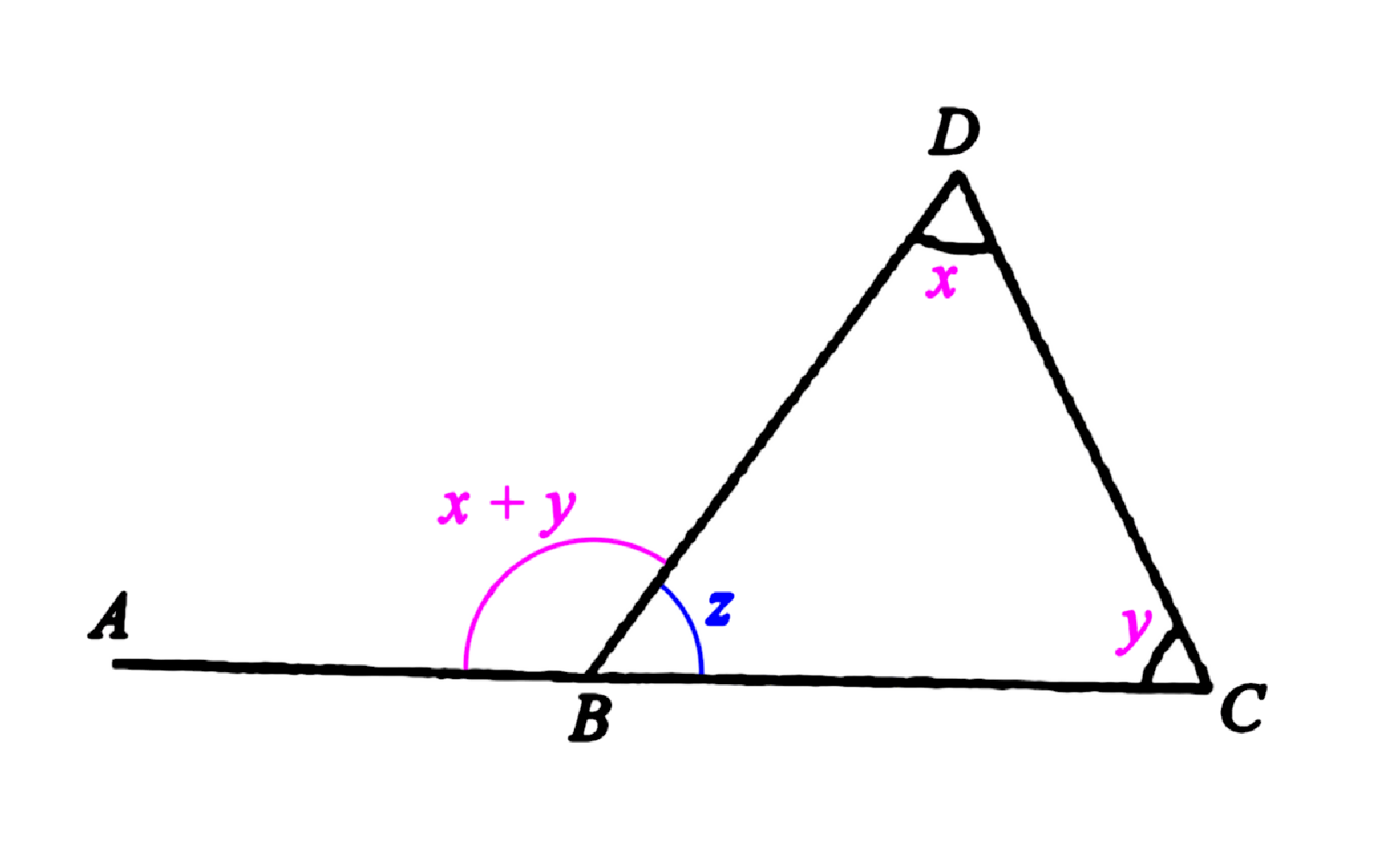
Have you heard of this? How do we know that this is always true? Well, the angle BDC = z, together with x and y will add up to 180°, being the sum of triangles. angle ABD and z also add up to 180°, as they are adjacent angles on a straight line. We must have angle ABD = x + y. Let us apply this to the problem posed.
Solution
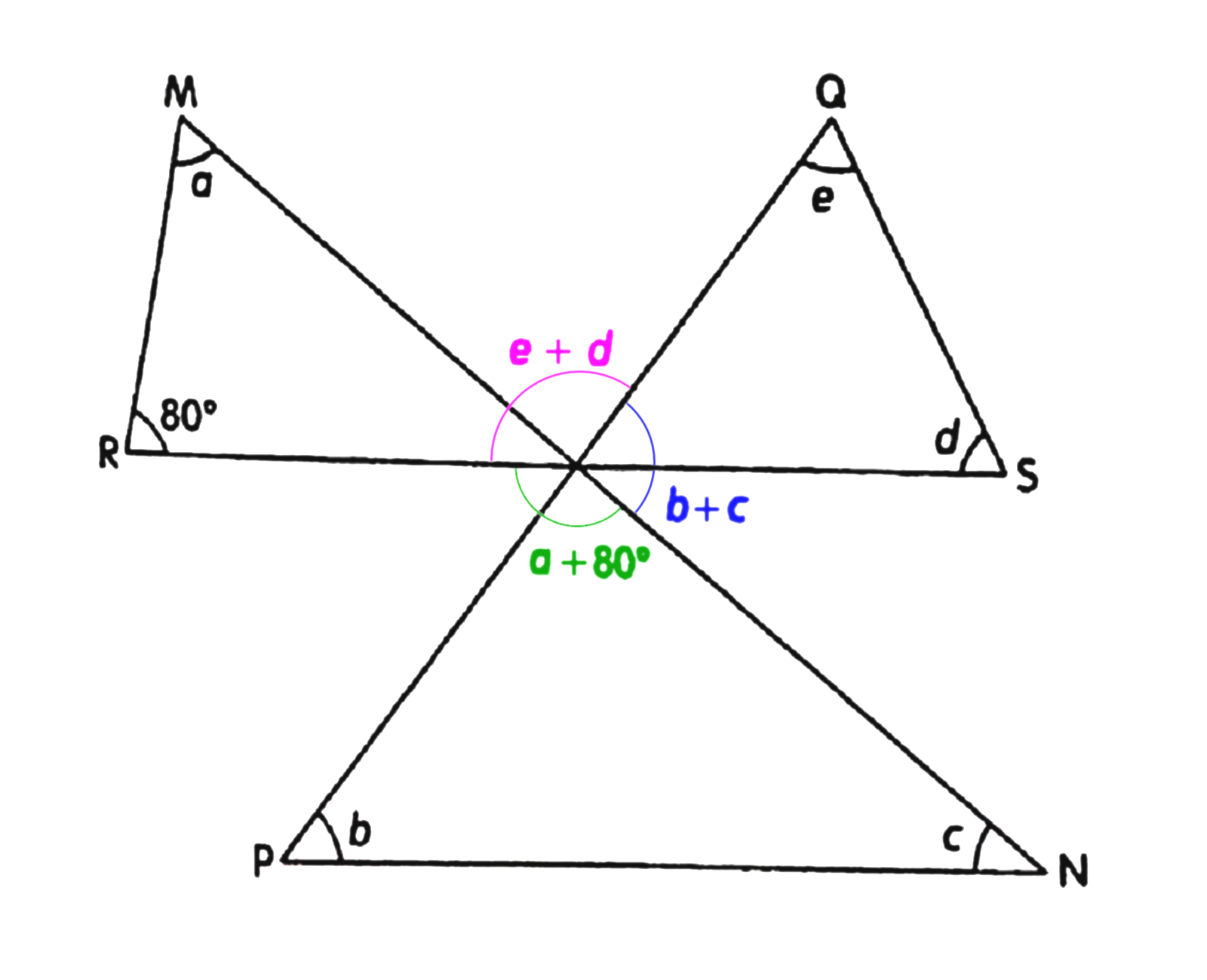
If we consider the external angles of the three triangles, we get a + 80° (marked in green), b + c (blue), and e + d (pink) and they all go round the common point. That means they add up to 360°. Thus (the measure of) the angles a + b + c + d + e = 360° – 80° = 280°. And that is the answer!
Reflection
It is good to do a reflection after every attempt to solve a mathematical problem, whether or not you succeeded in solving it. The army guys call it “After-Action Review” (AAR). It is actually an important part of the Problem-Solving and Learning Process. Actually, this is where we learn. Learning goes through four stages:-
- we don’t even know what we don’t know (or don’t even know that we don’t know) ... we are unconscious and maybe presumptuous
- we know that we do not know ... we discover the limits of our “knowledge” and realise that there is something more to learn
- we know that we know ... learning the stuff and becoming competent
- we do not know that we know ... we know it so well, that it becomes second nature, and do not even think about it
If we just passively listen to the teacher, we may think that we have “got it”, but the learner may not know that s/he does not know. This is stage 1. It is when you solve a difficult problem that you discover that you do not really know. This is stage 2. At least your radar is turned on and you learn. Stage 3. As for stage 4, that comes through a lot of practice, and it is good to have some variety in the practice. If we keep making the same mistakes on one type of problem, then more practice on that type of problem is needed. But if you have already mastered a certain type of problem, then get exposed to more challenging or different types of problems. Doing self-reflection and being self-aware (these are examples of metacognition) helps to steer us through the four stages of learning.
So what have we learned from solving this problem?
Let me share what I have learned from solving this problem.
Firstly, the exterior angle of a triangle thingy: it is equal to the sum of interior angles. OK, to be honest, I knew it already, but I tried using other ways of solving but could not think of any, and the other methods seem to point back to this “exterior angle equals sum of interior angles” concept. The exterior angles all fit nicely into 360°, leading to a short elegant solution, which is probably what the exam setter intended. Attempting to solve this type of problem can easily sprawl into many spurious dead-ends, getting nowhere.
Secondly, it is not necessary to know the individual values of the unknown angles a, b, c, d, and e in order to find their sum. Whatever values they have, the sum of the angles around a point is always 360°. This is true even if you changed the sizes of the five angles. That means that the individual values of the angles are unimportant. Sometimes in mathematics, we don't know some things, but it does not matter, so we do not need to know them! But realising that requires some "what if" thinking.
OK, so what have you learned from solving this problem? Is there any way other way of solving it? Please comment below.
@tradersharpe
-- promoting sharp minds
!originalworks
Announcement
Please join my mathematics contest. SBD to be given away!
