Shifting Goal-posts for the Limit?

This article is about an analogy and reasoning for understanding the technical definition of mathematical concept of "limits".

lim03 - goal posts.png

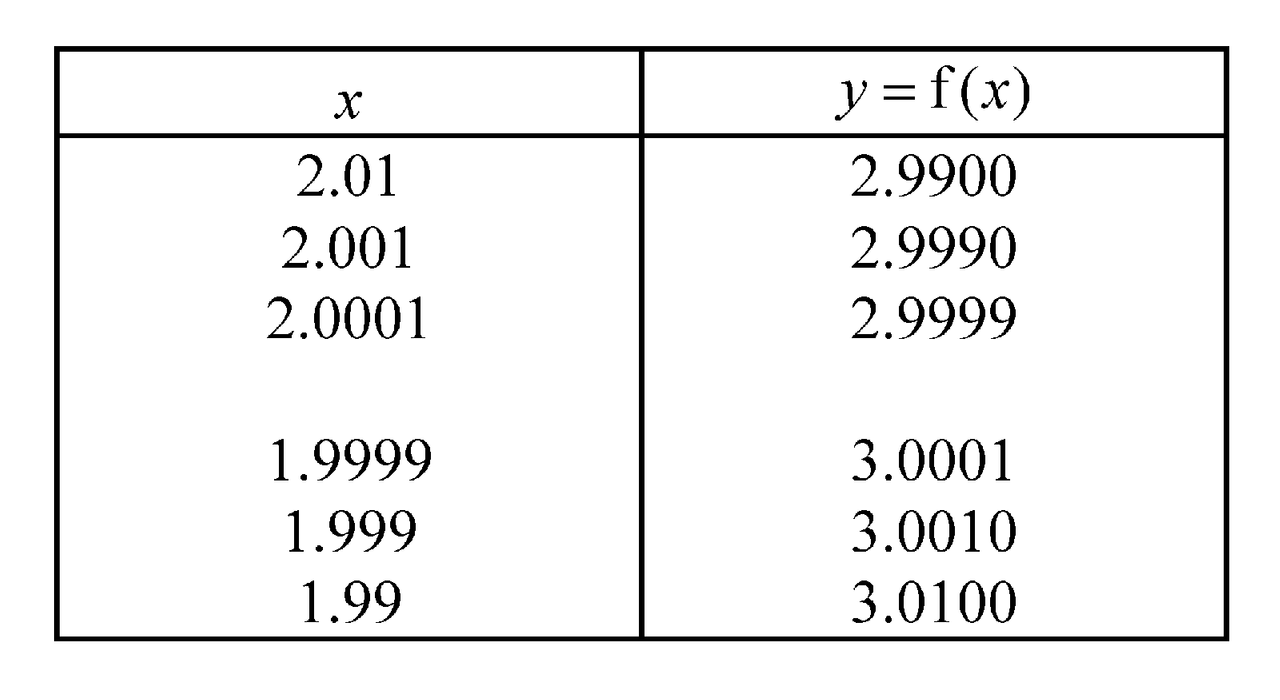
When students are first exposed to the idea of limits, they are told that limits are what the y values of an expression approaches, as x tends to a certain value. For example, if y=f(x)= ${4-\frac{1}{4}x^2}$ , then ${\lim_{x\to2}f(x)=3}$ . By calculation, we note that as x gets nearer and nearer to 2 (either above or below 2 but not equal to 2), y gets nearer and nearer to 3. Refer to the table.

lim01 - tablevalues.png

Then later they encounter the modern formal epsilon-delta defition of limits like this:-

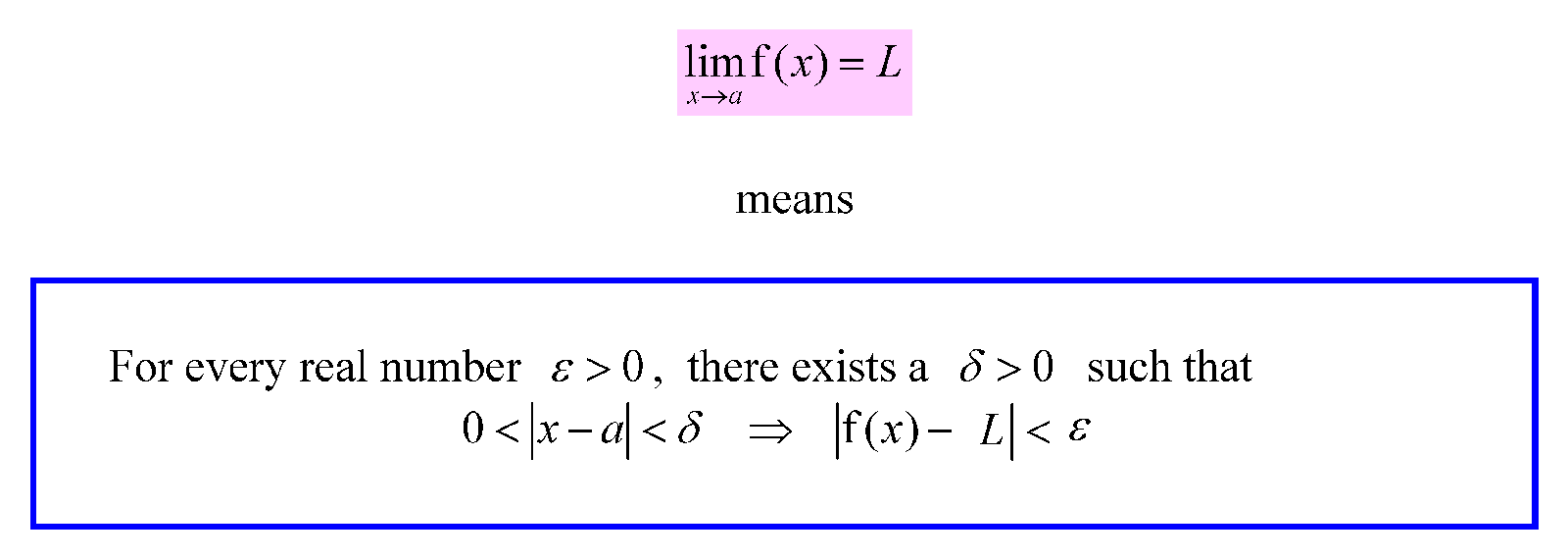
lim02 - epsilonDelta.png

Now students go “Wow! This is like greek to me!”. Do you know why it looks like greek to you? Because it is! Delta ( ${\delta}$ ) and epsilon ( ${\epsilon}$ ) are Greek letters that are sort of the counterparts to our letters 'd' and 'e'. But why use this complicated delta and epsilon stuff to deal with limits? The story goes that when Newton first invented his calculus, he had trouble explaining it. Or people found it difficult to understand him, especially his “infinitesimals”, which seemed like non-zero quantities that are small and yet treated like zero. This sounded contradictory. Later, other mathematicians like Cauchy (pronounced like “koshee”) were more cautious, and used the epsilon and the delta when dealing with limits. Some historians would dispute this, claiming that Newton did have a precise idea of limits in his writings.

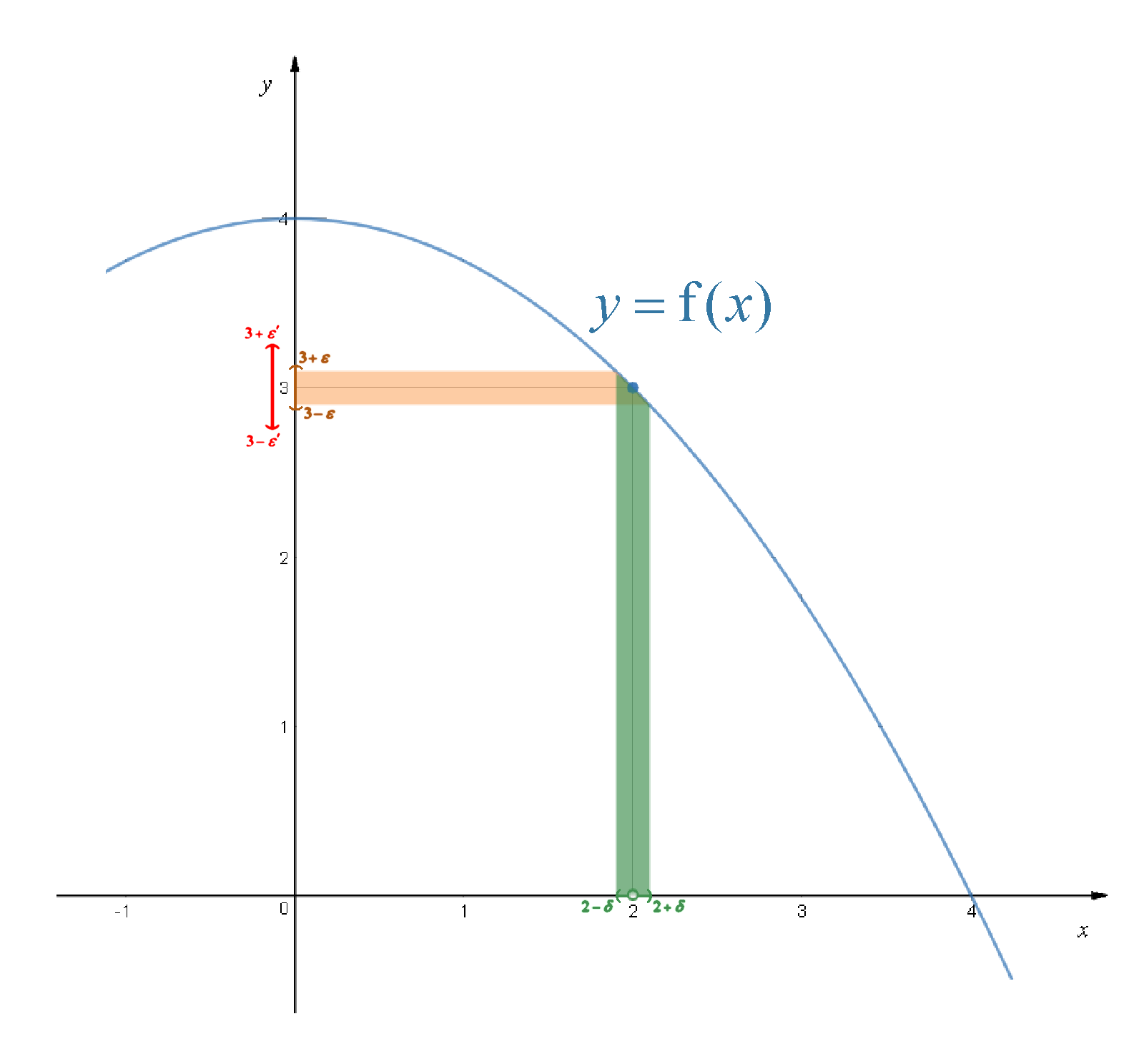
But what does that long bombastic definition even mean? The idea is that on the graph of y=f(x) epsilon ( ${\epsilon}$ ) controls the “error” on the y-axis i.e. the difference between the limit L and the y value, while delta ( ${\delta}$ ) controls the “error” on the x-axis i.e. the difference between x and a (x is equal to a). Take our above example where y=f(x)= ${4-\frac{1}{4}x^2}$ . No matter how small you specify the value of epsilon, you can always find an interval of x values near but not equal to 2 (at less than a distance delta away) that would map to and interval of y values near 3 (at a distance epsilon away). Let us imagine this is a kind of football (or soccer) where you put the tiny ball at a point on the x-axis and you shoot vertically towards the curve y=f(x) and the ball bounces and goes horizontally to hit the y-axis. The y values near 3 are between the “goalposts” ${3-\epsilon}$ and ${3+\epsilon}$ . I can find x values near but not equal to 2 i.e. between ${2-\delta}$ and ${2+\delta}$ that will shoot the ball in between the goal posts.

lim03 - goal posts.png

So epsilon is supposed to be “small”. To help students, some books do explicitly put in the words “no matter how small” together with “there exists an epsilon” in the definition. However, the more rigorous textbooks do not deem this necessary. My question is: why? In the formal definition, why is it not necessary to mention that epsilon is meant to be small? Look at the diagram again. Think about it. Epsilon controls the width of the goal posts. If you had wider goal posts, of width ${2{\epsilon}'}$ , then of course you would be able to shoot in between the wider goalposts ${3-{\epsilon}'}$ and ${3+{\epsilon}'}$ , if you can shoot within a width of ${{2\epsilon}}$ . Formally, this is from the Law of Transitivity for inequalities. If ${|{f(x)-L}|<\epsilon}$ and ${{\epsilon}<{\epsilon}'}$ , then ${|{f(x)-L}|<{\epsilon}'}$ . "For all values of epsilon" means all the values including the "small" ones.The big values are not a problem. The issue for the limit is that even if you keep on making epsilon smaller and smaller, can you still shoot in between the goalposts?

I hope this article helped in deepening your understanding of limits, especially its epsilon-delta technical definition.

Cheers!