My article on Visualising the Division of Fractions is spreading like wild fire on social media. The basic idea is that when you divide by a fraction (e.g. half), we are counting with smaller units (e.g. the halves), so we get proportionally more in number (e.g. double) to compensate. This is why we multiply.
Did you notice that I purposely chose simple examples to ease everybody into that idea? All the examples I gave were divisions by unit fractions, which are fractions with 1 as numerator.
What if the numerator is not 1? This is what we are going to discuss in this article.
Example 1
Let us say you want to know the meaning of . To visualise this, we draw 4 bars. Since we are dividing by two-thirds, let us subdivide each of the 4 bars into 3 equal smaller pieces (thirds).
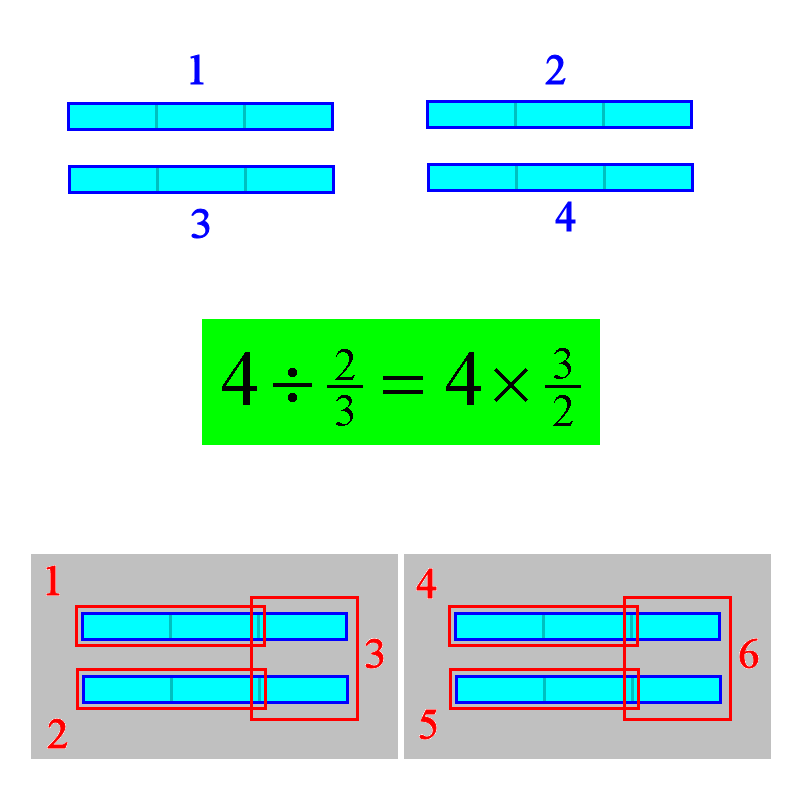
What does dividing by two-thirds mean? You take every two of smaller pieces (thirds) and group them and treat that as your new unit (indicated in red in the diagram). So how many groups of two smaller pieces are there? Notice that every 2 original whole units comprises 6 thirds, and that forms 3 groups of two small pieces. Observe that
(1) The ratio of the size of each new unit compared to the size of each old unit is 2:3.
(2) The ratio of the number of the new units to the number of old units is 3:2, the inverse ratio.
And that is why the number 4 of original (blue) units is multiplied by .
You have smaller units (red) than the original units (blue). To compensate, the number of smaller units is proportionately more.
Example 2
Let us look at a slightly harder example. Let us say you want . You pre-divide each original unit (shown as blue pentagons) into 5 equal smaller triangular pieces. Each small piece is one-fifth of the pentagon.
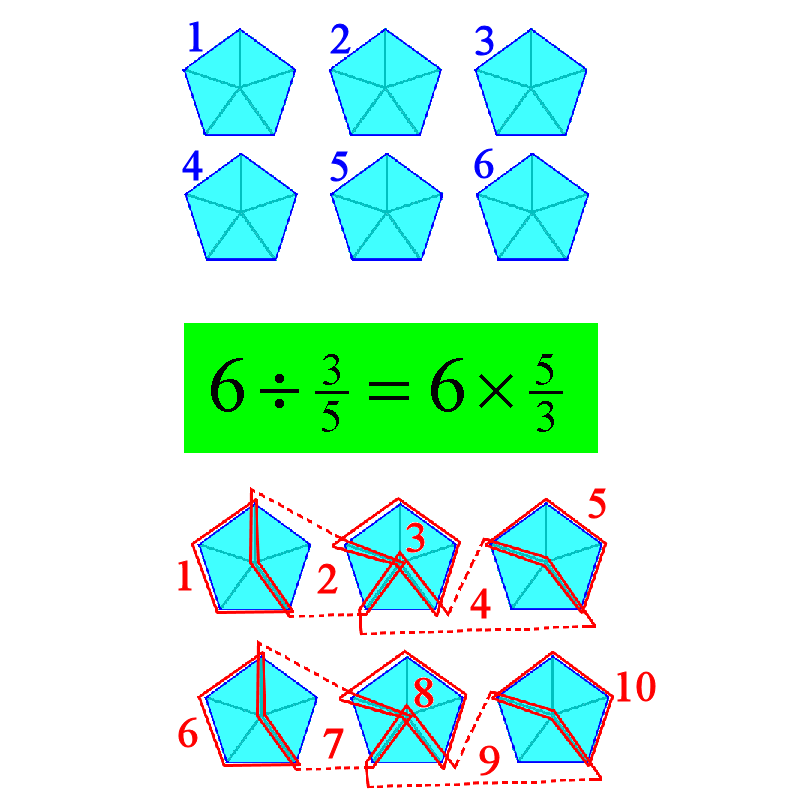
Since we are dividing by three-fifths, we take every group of 3 of the small pieces as our new unit, and then we count the number of such groups. It can be a little tricky, as we might need to take small pieces from another pentagon to form a group of three pieces. But it can be done. Every 3 pentagons (blue) give rise to 5 new groups (red), as they both contain 15 small triangular pieces. So we see that
(1) The ratio of the size of each new unit compared to the size of each old unit is 3:5.
(2) The ratio of the number of the new units to the number of old units is 5:3, the inverse ratio.
And that is why the number 6 of original (blue) pentagons is multiplied by .
You have smaller units (red groups) than the original units (blue pentagons). To compensate, the number of smaller units is proportionately more.
Example 3
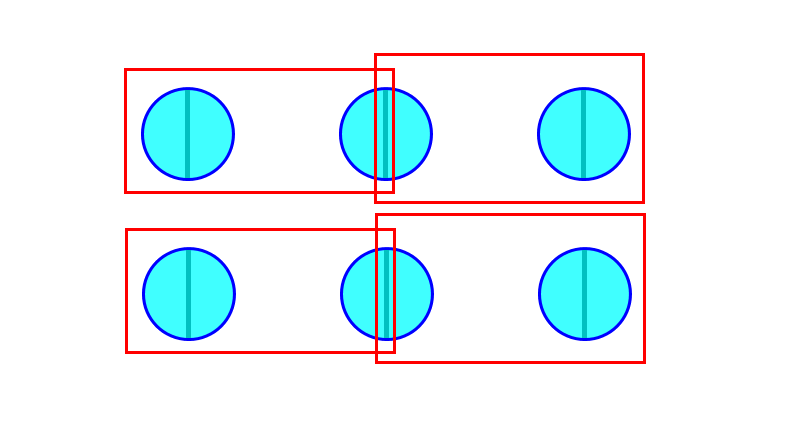
For our pièce de résistance (or is it coup de grâce?), we shall consider division by a fraction greater than 1. For instance, let us look at . Actually this is easy. If we have 6 circles, say, we first sub-divide them into halves.
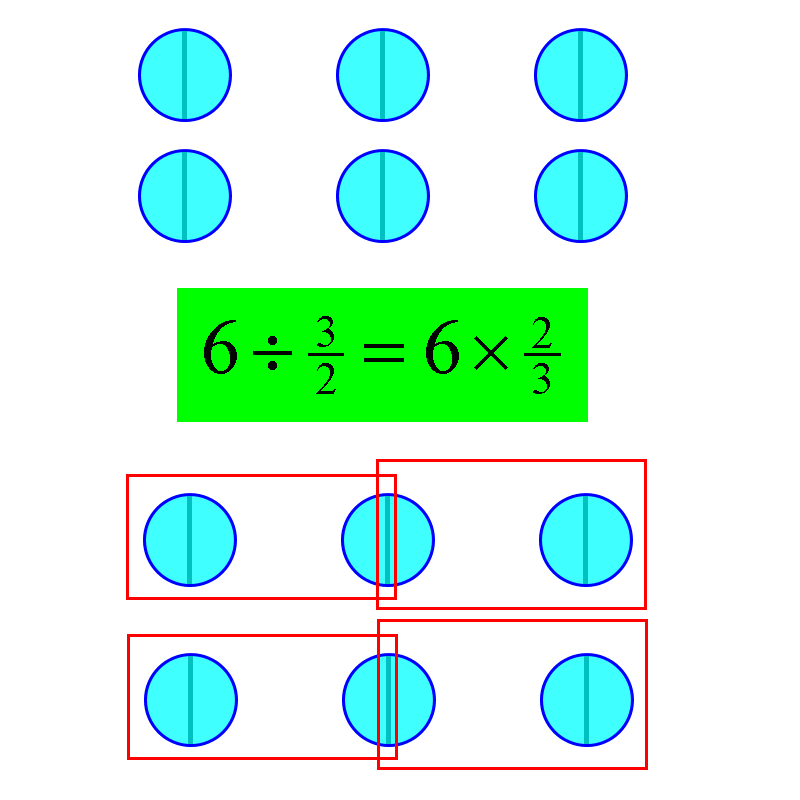
Division by 3/2 just means every group of 3 halves forms a new unit (shown in red). Then we just determine the number of such groups. Every 3 circles, constituting 6 halves, gives rise to 2 such groups. Hence
(1) The ratio of the size of each new unit compared to the size of each old unit is 3:2.
(2) The ratio of the number of the new units to the number of old units is 2:3, the inverse ratio.
And that is why the number 6 of original (blue) circles is multiplied by .
You have larger units (red groups) than the original units (blue circles). To compensate, the number of red groups is proportionately less.
In general, we have
And this is the reason why you flip the fraction. The principle still remains: If you have larger new units, there will be proportionally fewer new units. If you have smaller new units, there will be proportionally a greater number new units. Since the relevant proportions are inverses of each other, the number of new units can be calculated via multiplying the reciprocal (inverted fraction) of the divisor.
So teachers, parents, students, citizens of the world!
Now you know the reason why,
Therefore invert and multiply!
Cheers!
Announcements
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Please join my Sharp Mathematics Contest 2, which is based on the discussion in this article. Resteem and tell all your friends about it!
Cheers!!!
@tradersharpe
-- promoting sharp minds
