We've been discussing the meteoric resurgence of people who believe in a flat earth, and one of their many proofs of claim (when they have any at all besides just declaring the earth is flat and denying any evidence to the contrary) is that, if we lived on a sphere, mountains and buildings should appear to be leaning away from us. We are not talking about the rare exceptional building, such as the leaning tower of Pisa, or one, like the Capital Gate in Abu Dhabi that was built to lean, but the average building, such as a skyscraper, that was built well and is 'plumb', or at a 90 degree angle, to the ground.

Capital Gate Building in Abu Dhabi
Courtest of Wikipedia.com
It's true, if a building is far enough away from a person, or another building, the objects would, indeed, lean away from us on a sphere the size of the earth. Flat earthers love to illustrate this concept in a mocking fashion,with drawings that appear to have been done by a 7 year old.
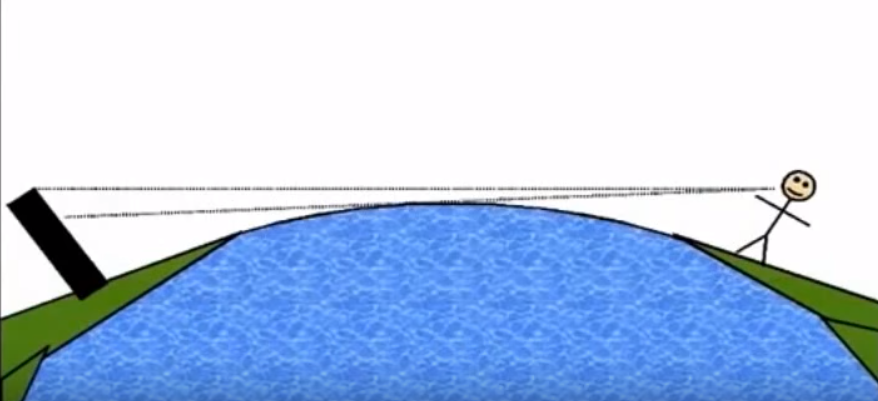
Image Credit: Just a meme
While the CONCEPT in the drawing is correct, what flat earthers do not seem to understand is the math and the scale. They seem to think that because they made the drawing look like the building is leaning at a 45 degree angle, then even a building 20 or 30 miles (32-48 km)away should be leaning at a 45 degree angle away from them!
Anyone with any degree of understanding of the size of the earth, however, would understand that this drawing, if it were to scale, would represent a building and person who were as high as outer space and more than a thousand or more miles (1600 km) away from each other!
Buildings Should and Do Lean Away From Us
As I said, the concept in the drawing is correct; since we live on a sphere, buildings far away from us actually do lean away from us. This is because, if you drop a plumb line from a building, it will drop at a 90 degree angle from the building (assuming the building actually is at a 90 degree angle to the ground, as most, but not all buildings are).
Image Courtesy of Wikimedia Commons
Now imagine, you are viewing two similar buildings from a distance, each of which is equidistant from you, and each of them plumb to the earth. If you could 'slide' these buildings further and further away from each other, eventually, the curvature of the earth will come into play and the buildings will lean away from each other. So, yes, flat earthers are correct in that the buildings should lean away from us and each other like the observer and the building do in the flat earther drawing above.
However, one problem with flat earthers is that they tend to have lots of expectations about what they should see or what should occur on the a globe the size of the earth without having actually figured out the reality of such things. In other words, they fail to fact check what actually should occur and simply consider their belief system a fact. This occurs over and over again when talking with flat earthers, and for some reason they will resist any and all facts contrary to these erroneous expectations they literally pull out of their imaginations.
Correcting Expectations
How much the buildings should lean away is the question that flat earthers should have asked before making a claim about buildings leaning in the first place, but since they don't, we'll have to answer the question for them since they are not inclined (pun intended) to do it themselves.
To proceed, we have to do some simple math, something flat earthers often think was put on earth to fool or control people (not joking), although they will happily use math formulas they don't understand incorrectly and in the wrong situations if they think it supports a case for a flat earth.
The earth is a 360 degree sphere, with a circumference of between 24812-24900 miles (39931-40072 km). I'll use the 24812 miles number to be biased towards having more lean than less, even though the difference will be miniscule.
So the VERY VERY easy math that flat earthers don't bother to do is to simply divide 24812 miles by 360 degrees to get how many miles we would need to be away from an object for each degree of lean.

Image Courtesy of Pixabay
That gives us 68.9 miles (110.8 km) for every one degree of lean on a sphere the size of the earth. So, for every 68.9 miles distant you are from a building, you would expect to see it lean ONE SINGLE DEGREE. Even the world record longest land to land photography image, at just over 300 miles (482 km), would only show an approximately 4 degree lean.
The Next Question Flat Earthers Haven't Asked
So, first of all, you'll need a telescope to see buildings in any amount of resolution at 70 miles because they will be so small. Next, instead of making assumptions, we need to determine if we can even visualize a one degree lean.
You can test this for yourself, via either a real experiment or a thought experiment. Take two pencils and a bit of foam, clay, or play doh. Use a protractor to get the first pencil to stand at an exactly 90 degree angle. Take the second pencil and stand it next to the first pencil at an 89 degree angle. Now, walk away a couple of paces and look back at the pencils. You could do the same by putting two water glasses side by side and angling one side with napkins or toothpicks until you get the one degree lean the experiment requires.
Results of the Experiment
Did you see the lean on the pencil or the water glass that is leaning? Heck, you probably didn't even bother to do the experiment because it's so ridiculous. Even if you DID do the experiment, I suspect you would have found it extremely difficult to even measure the one degree difference, let alone see it. The eye is simply not that sensitive of a measuring instrument.
An even better experiment is to go look at the leaning tower of Pisa and look at it where the lean is away from you and not to the side. If you can visualize a lean at all, it will be extremely slight, even though the tower is leaning at almost four degrees, about the same lean as the world record photography distance. These slight leans, particularly when they are leaning away from us, are simply too slight to see.

Image credit: Wikimedia
Perhaps one might think it would be easier to see objects lean away from each other with the observer looking at two objects far away from each viewing them from the side, as in the drawing above. That produces other challenges, however, since the visual angle of a camera and the eye is too narrow to capture objects that are far away from each other in high enough resolution to see them clearly. That's why the panoramic function on cameras was invented.
For instance, you might think an image of the Chicago skyline might be a good way to visualize the lean of buildings away from each other, but this panorama of Chicago only encompasses about a mile (1.6 km) of the city! That is far too small to notice any lean.

Image credit: Chicago Inno under a fair use claim
Even though we discuss why our senses fool us in the article Should We Really Trust our Senses, flat earthers seem to think they should detect the most minute change in just about anything, such that if they cannot physically see the change they will declare it non-existent without measuring it, and declare it 'science' to have done so.
Yes, buildings SHOULD lean away from us on a sphere the size of the earth, but not to any degree noticeable by the human eye and cameras are simply not going to have a wide enough field of view to be able to detect or measure any lean of buildings or objects away from each other. And the panoramic function on a camera would correct for any lean in order to make the image appear straight anyway.
This is simply not a way that we can determine whether the earth is flat or round because we would not be able to visualize buildings leaning away from us on a sphere the size of the earth. I believe any rational person would be able to understand this through the evidence that has been presented here.
The problem is that flat earthers are not rational, so will reject this rational and easy to understand proof for ridiculous reasons, such as that math is from the Illuminati or the Freemasons, and so you can't trust the simple math I showed here! I really couldn't make that up if I wanted to.
