
New, old, and exotic musical scales are being mastered by more and more composers and improvisers. They want pitch interval systems that make sounds that cannot be made in ordinary chromatic tuning. Catch up with them by getting acquainted with cents, in the first of my Busy/Steemit “tuning notes.”
Cents are a convenient unit of measure you can use to quantify the tuning or mistuning of musical intervals.
Ordinary chromatic tuning is favored by a vast musical majority, found in every nation on Earth. It has “12 equal” semitones per octave. If all 12 notes are used, all 12 keys have the same harmonic, melodic, and modal resources.
Each succeeding pitch in “12 equal” semitone temperament has a frequency that is higher than the last by the same factor, multiplying the previous frequency by 2^(1/12), which can also be written ¹²√2, meaning the 12th root of 2. This 2 is important.
Most musical scales recur every “octave” such that notes an octave apart are treated as the same note. This “octave” is thus the repeating frame interval for most musical scales. It also occurs in the birdsong of some but not all avian species, notably the uirapuru or musician wren. And the “octave” is the loudest overtone in musical instrument voices with so-called “harmonic” timbres. Although its name likely reminds you of the number 8, it is really the number 2. An “octave” down is just frequency halving, and an “octave” up is just frequency doubling.
“Logarithms” are exponents of a numeric base, exponents that let you substitute addition for multiplication, and subtraction for division. Pitch perception among humans (and musician wrens?) is logarithmic. For musical scales that use the octave as a repeating frame interval — in other words, for most musical scales — the ideal numeric base for these logarithms is base 2.
With frequencies, each succeeding pitch in the ordinary chromatic scale multiplies the last frequency by 2^(1/12). In that multiplier, 2 is the base, and 1/12th is the exponent. 2^(1/12) is an irrational number, which is just about 1.0594631. Yet its base-2 logarithm is rational. It's 0.083̅, where the 3̅ keeps repeating, which is merely the decimal way to say 1/12th. Multiply that logarithm by twelve and you get one. Because one is a natural number, it is more easily added to another number than 0.08333333… is.
With twelve (as the scaling factor) times the base-2 logarithm, each succeeding pitch adds one semitone to the last, and adding twelve semitones takes you up to the octave. However, a semitone, 1/12th of an octave, isn’t a very small interval by microtonal standards. It doesn’t allow for very fine tuning.
So now, instead of multiplying base-2 logarithms by twelve, multiply ’em by twelve hundred. Instead of giving you semitones, that gives you cents. Using cents allows you to tune with high resolution, a hundred times finer than using semitones.
Above, the frets on this guitar fretboard are all spaced an equal semitone apart. Because pitch is logarithmic, higher frets (right) are closer together than lower frets (left). This picture and the treble clef thumbnail near the top are CC0 images from Wikimedia.
There are 100 cents in a semitone, and 1200 cents in an octave.
The ordinary chromatic “12 equal” semitone temperament, 12 “equal divisions of the octave” or “12edo” or “12ed2,” has a simple structure when its intervals are listed in cents. All of its pitch intervals are multiples of 100¢, ending at the 1200¢ octave. Whether you like this tuning as a musical paradigm or not, it is at the very least an excellent reference grid for quantifying other tunings.
According to tuning expert and software designer Joe Monzo, the ancient Sumerians, due to their base-60 number system, could have approximated 12edo before the year 1750 BCE. Others have suggested that Aristoxenus of Tarentum, who flourished in 335 BCE, might have done so, though I doubt this.
By 1585 CE, Zhu Zaiyu (朱載堉) in China and Simon Stevin (or Stevinus) in the Netherlands had attempted to calculate and utilize 12edo. Matteo Ricci, the famous Jesuit visitor to China, helped make 12edo tuning known in the West. Another prominent Western advocate was Galileo’s father, the Italian lutenist and luthier Vincenzo Galilei.

Above, Peterson tuner on a Tonal Plexus keyboard by Hπ. Separately, both are useful for playing in exotic, old, or new tunings. Photo by the author.
When the string, the pipe, and/or the reed lengths — and therefore the pitch frequency relations — of a tuning involve simple ratios of small natural numbers, then that tuning belongs to a category known as just intonation. Most, and maybe all, ancient scales were of this type. Just intonation tunings have their advantages, but their intervals between adjacent notes are unequal. As with other unequal tunings, this means their different keys have different harmonic, melodic, and modal resources.
In an unequal tuning, modulating or transposing a musical piece or a part thereof into a different key can be a problem. It may ruin a chord or sequence by introducing a dissonant “wolf” interval where a harmonious interval belongs.
The 12edo pitch interval system was introduced because it comes close to some just intonation scales while allowing full freedom of transposition and key modulation.
One just intonation scale closely approached by 12edo is called the Pythagorean scale, even though it may have entered history much earlier than Pythagoras. Generated by the 3/2 “perfect fifth” interval, or by its 4/3 “perfect fourth” inverse, the Pythagorean scale puts powers of 3 into ratios with powers of 2. It was developed in an era when only the 2nd and 3rd harmonics — the two loudest overtones in the voices of instruments with harmonic timbres — were considered consonant.
Here is a table using cents to compare the Pythagrean scale with 12edo.
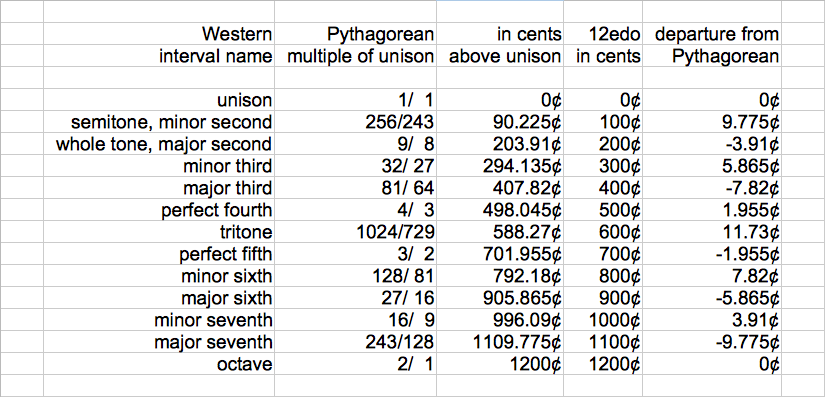
Except for the tritone, every 12edo interval comes within 10¢ of its Pythagorean counterpart, at least in this mode. That's because 2^(7/12), at 700¢, is very close to the Pythagorean generator 3/2, at 701.955¢ (which is obtained through taking the base-2 logarithm of 3/2 and then multiplying that by 1200). A tuning difference of only about 2¢ is very hard to hear. It cannot be heard at all in sequence; it can only be heard in simultaneous play. Thus it can be said that the ordinary chromatic 12edo tuning has a “near-just” 3/2 and its inversion, a “near-just” 4/3.
Old Chinese culture, centuries before the birth of Zhu Zaiyu, also used a just intonation scale, which is really the Pythagorean scale in a different mode, taking the tritone in the table above and making it the unison from which the rest of the scale rises. Here is a table using cents to compare this Old Chinese scale with 12edo.
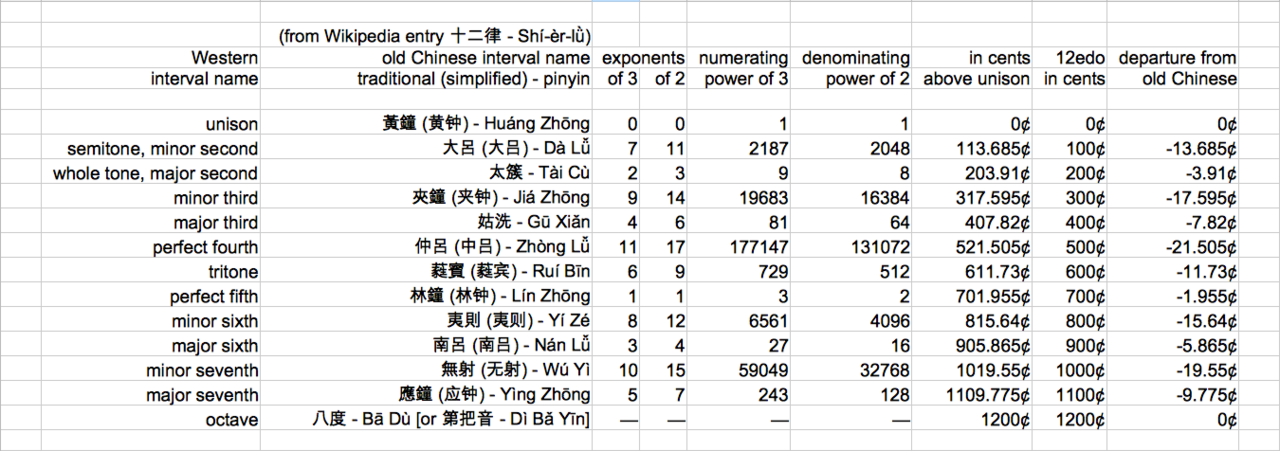
In this mode, the powers of 3 are all numerators and, except for the repeating frame interval at the octave, the powers of 2 are all denominators. No inverse generators are used. This maximizes the divergence between just and 12edo, right at its oddball variant of the “perfect fourth,” which is not 4/3 here — remember, no inversions in this mode — but, instead, 3¹¹/2¹⁷ or 177,147 over 131,072.
Beginning in medieval times, and spreading all around the Mediterranean by the Renaissance, musicians began to recognize the 5th, the 7th, and even higher harmonics as consonant. In the overtone structure of harmonic instrumental timbres, the 5th harmonic is the loudest of these. Folded into the octave, it was realized as the 5/4 interval, which replaced the old Pythagorean value of 81/64 as the “major third.” Likewise the inverse of the 5th harmonic, 8/5, replaced the old Pythagorean value of 128/81 — not to mention the old Chinese value of 6561/4096 — as the “minor sixth.” These changes made the major third and minor sixth sound sweeter.
At this point we need to skip over a few centuries, when vital, crucial developments in the history of tuning occurred, and talk about the Ellis duodene. This is another JI scale with 12 notes per octave, incorporating multiples and ratios of 5, powers of 3, and powers of 2. Actually, it is only one of several duodenes that A.J. Ellis described in the 1870s, and the JI values in it date back to the centuries we just skipped over, yet it is termed the Ellis duodene anyway. Here is a table using cents to compare it with 12edo.
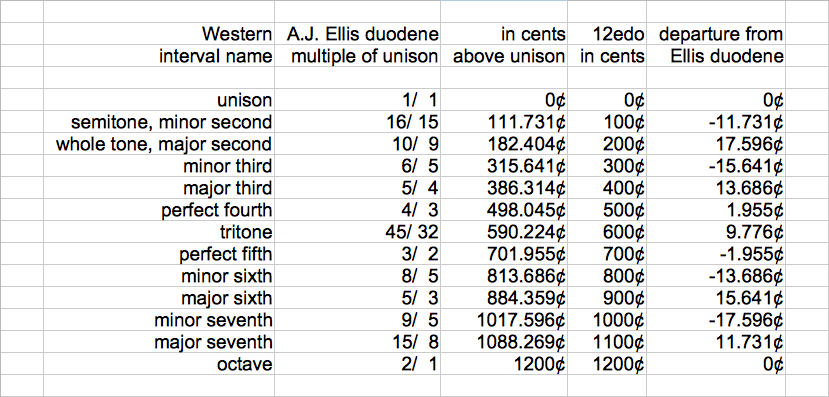
As you can see, 12edo does not approximate the ratios involving 5 or its multiples very precisely. Still, every 12edo interval comes within 18¢ of its Ellis duodene counterpart, at least in this mode. In fact, the worst approximations in the table are the 12edo whole tone and its inversion, the minor seventh. Both of these go astray from their Ellis duodene values by nearly 17.6¢, yet keep within 4¢ of their Pythagorean values.
The Pythagorean whole tone of 9/8, or major whole tone — and the Ellis whole tone of 10/9, or minor whole tone — can be taken as rational outposts near the extremes of the whole tone category. Because the 12edo whole tone sits between them, 12edo is regarded as one of several “meantone” scales. Meantone tunings are among the vital, crucial tuning developments of the Renaissance that we skipped over.
Meantone tunings narrow the “perfect fifth” by a few cents, making it depart from 3/2 slightly in order to sweeten other intervals. They also widen its inversion, the “perfect fourth,” likewise.
The interval between the Pythagorean major third, or 81/64, and the Ellis duodene major third, or 5/4, is the ratio 81/80, known as the syntonic comma. Its value is about 21.506¢. Meantone tunings approximate JI scales in such fashion as to “temper out” that interval.
If a meantone tuning narrows the perfect fifth (and widens the perfect fourth) by a quarter of a syntonic comma, or about 5.3765¢, then the major third will be a sweetly precise and exact 5/4 interval, and the minor sixth will be a just 8/5. This tuning is called “quarter comma” meantone, and — as was noticed in the Renaissance by Nicola Vicentino — is virtually identical to 31 equal divisions of the octave.
A great example of quarter comma (31edo) meantone is at this link, which is not my work but that of Stephen James Taylor.
If a meantone tuning narrows the perfect fifth (and widens the perfect fourth) by a third of a syntonic comma, or 7.1686̅¢ where the 6̅ keeps repeating, then the major sixth will be a sweetly precise and exact 5/3 interval, and the minor third will be a just 6/5. This tuning is called “third comma” meantone, and — as was noticed in the mid-1500s by Gillaume Costeley and Francisco de Salinas — is practically the same as 19 equal divisions of the octave.
A truly lovely example of third comma (19edo) meantone is at this link, which is not my work but that of Aaron Krister Johnson.
If a meantone tuning narrows the perfect fifth (and widens the perfect fourth) by a fifth of a syntonic comma, or about 4.3012¢, then the major seventh will be a sweetly precise and exact 15/8 interval, and the semitone or minor second will be a just 16/15. This tuning is called “fifth comma” meantone, and — as was announced in the early 1700s by Joseph Sauveur — is practically the same as 43 equal divisions of the octave. Sauveur wanted to quantify tunings and mistunings with units based on 43edo and its multiple 301edo, instead of cents.
After 12edo, the octave divisors that best approximate the 3/2 “perfect fifth” interval are 29edo, 41edo, and 53edo. None of them are meantone tunings, but they closely resemble extended Pythagorean tunings. The smallest octave divisor that is nearly exactly just in every interval of the Ellis duodene is 53edo.
Many, many, many other octave divisors have been used in making fantastic music. Some of the most important include 9edo, 10edo, 11edo, 13edo, 15edo, 16edo, 17edo, 22edo, 24edo, 26edo, 34edo, 37edo, 50edo, 58edo, and 72edo. Non-octave scales can also produce great music.
A fine 10edo song can be found at this link, which is not my work but that of Elaine Walker.
A hilarious and insightful 22edo piece can be found at this link, which is not my work but that of the group Metaclown Xendustries.
A multiple of 41edo, namely 205edo, includes a quarter-comma meantone tuning, nearly just versions of all the Ellis duodene intervals, and the almost Pythagorean tuning represented by 41edo itself. Also encompassing numerous other scales of great potential, 205edo is the default master tuning of the Tonal Plexus keyboard. Its finest gradation of pitch is 2^(1/205), which is about 5.854¢, represented by the difference between vertically adjacent buttons on the keyboard. Buttons with concave bowl tops play 41edo notes.

Above, button heights and contours make the Tonal Plexus keyboard much easier to navigate by touch than it may appear. Black and white colors indicate the closest notes to the ordinary chromatic scale. The Plexus was designed and built by Aaron Andrew Hunt. Photo by the author.
Although this could be changing, most people who tune instruments are still not interested in any tuning except ordinary chromatic 12edo. For them, cents measurements are useful only in helping them “zero in on” the pitches of that one conventional scale. Tuning devices like the Peterson unit shown here are designed to meet their needs, while also accommodating those who also want to realize newer, older, or more exotic scale possibilities.

Above, Peterson V-SAM virtual strobe audio metronome tuner, tone, and rhythm device. It can show pitch tunings and mistunings in cents. Photo by the author.
a few words about me
Follow • Upvote • Resteem — if you like!
