Mikhael Gromov. IHÉS Paris. June 26 of 2007[1]In the 1960's, chemists[2] found that when denatured proteins unravel but when they cooled off they returned to their original shape. Like a coil, but this was not dependent on deformation like with the coil or by the internal machinery of the cell but by the particular nature of the amino acids.
Proteins are nanomachines. They perform at extremely high speeds and with a different paradigm for energy use when compared to macro-machines. The way they create work is by changing their shape. A property resulting from the interaction among the amino acids that conform them.
More formally, proteins are chains of amino acids joined by peptide bonds. They have different spatial structures. As I've mentioned before, form and function go hand-in-hand in biology, so predicting and designing reliably new structures would impact the function of these proteins.
The ProblemsComputational biology is hard. So hard that is most common for new mathematical structures to appear from biology than the opposite. I'll explain why. There are two problems one must approach. The first is the structure prediction of proteins starting from genome sequences to arrive at macromolecular structures. The second is the design problem where one starts with a macromolecular structure one wants to make to arrive at a genome sequence.[3]
Currently, there are 4 levels of classification based on their similarities as classified by the SCOP.
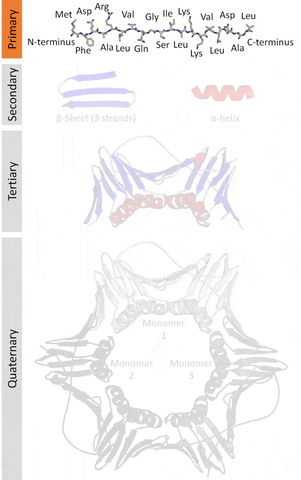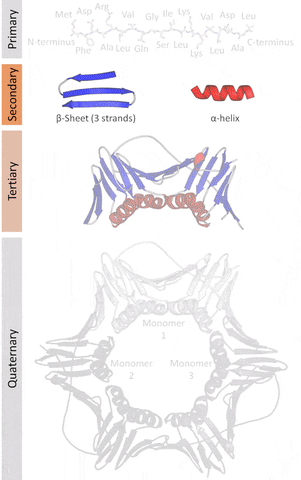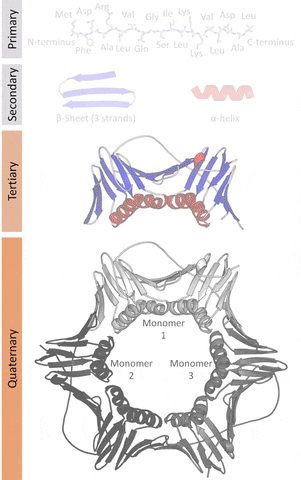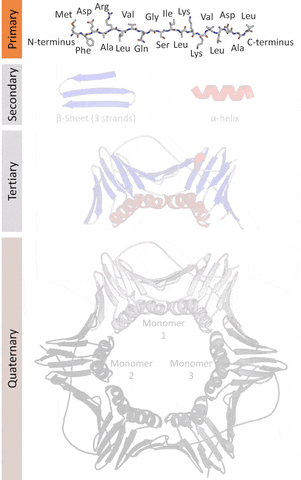
The native structures of proteins are probably the lowest energy states for a protein sequence in their solution medium, like inside cells. This is known as the folding funnel hypothesis. For each amino acid, there's a different level of low energy that affects the overall end result.[4] So the problem of design is how do you go from the unfolded-high energy state to the folded-low energy state?
This is a computational problem of astronomical complexity. Is a really hard problem.
For each amino acid in a protein chain, there are several rotatable bonds, around 3 for each amino acid. ≅3n. This means for a peptide of 100 amino acids (a small protein) you have 3100 possible configurations. If this wasn't enough, the number of protein sequences depends on the particular amino acid residue (out of the 20 amino acids) and their position in the chain .[5]
This means the possibilities are 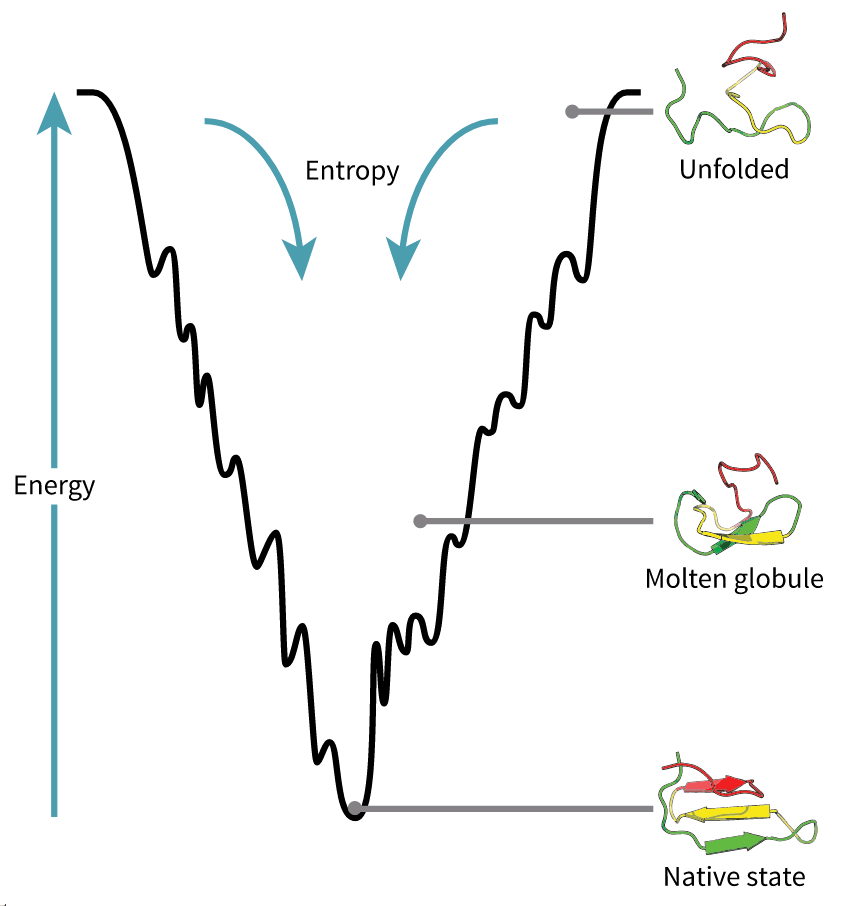 For the secondary structure, you need to calculate the lowest energy of the individual atoms in the proteins and the atoms of the surrounding water. To determine how the protein structure will collapse in a water solution and reach their low energy state a.k.a. native structure. This requires finding the Gibbs free energy and the geometrical optimizations that although hard are more tractable problems.[6]
The tertiary structure is a simpler problem (still hard), as it depends on apparently a limited set of tertiary structural motifs (e.g. helix-loop-helix motif that is a super secondary structure), approximately 2,000 distinct foldings.[7]
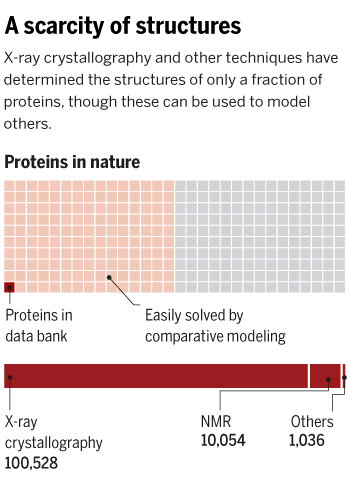
 After the success of the Human Genome project, the sequences of proteins that come out each day far surpasses the limit of characterization possible by X-ray Crystallography or by NMR-Spectroscopy, which limits brute force approximations. This geometrical problem extends depending on the packing of the side chains.
The cost and intensity of characterization of proteins by imaging techniques is a huge limitation in the field. So it's a pleasant surprise just many structures are being characterized thanks to modeling. The quaternary structure is a lot simpler. It can already be predicted with high accuracy for protein complexes. As protein-protein interaction prediction by the study of flexible and rigid macromolecular docking, thanks to an arduous inductive and modeling work in intracellular pathways and biochemistry. The crowdsource nature of this approach is bearing fruits.
The Engineering ApproachOther fields of science and industry have almost sucked dry the field of biology out of people with training in engineering, maths, and physics. For a long time, the lack of people from these fields was not really noted until recently, when computational progress and information theory have interconnected all fields more than ever.
For instance, in the field of medicine, most of the developments in tools for tissue replacement have been engineered by doctors themselves. This done with tools they find at home that is not necesarily the best for the human body. Slightly shameful are the examples of naive materials science:[8]
Fortunately, thanks to the outsourcing to engineering much better alternatives are being found. Although the economic incentives in the industry and existing materials will take some time to be replaced.
Information gain has mainly been possible thanks to mathematical modeling of gene sequences and advancement in 3D graphics.
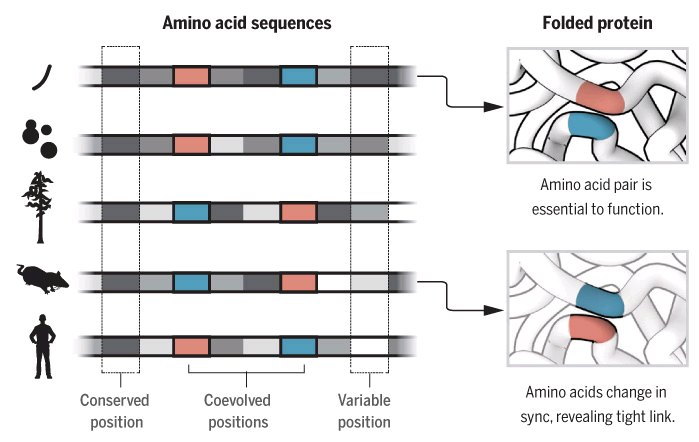 One of the first guesses for proteins bigger than 100 amino acids, was that a particular combination of amino acids occurring a certain number from each other would start a folding pattern. They were tracked by following amino acids that would end up spatially close or together in the final 3D structure. If this was true, a mutation in the gene sequence would also alter this particular combination to keep the structure. [9]
The comparison of homologous proteins across species gave a strong hint that this was true. As changing the position of one of those amino acids rendered the protein useless but changing both in sequence so they ended together conserved the function.
In design, an idealized version of general proteins is achieved. This is done by calculation of the optimal amino acid sequence for the desired protein. Then from the amino acid sequence a back translation to DNA. Design the gene that encodes the desired protein. Put it into bacteria, purify the protein and then solve the structure by crystallography. Basically, reverse engineering. Not surprisingly, this allows super-precise calculations with atomic level accuracy[10]
As evolution is a conservative process there's a lot of baggage in the formation of proteins due to this. Designed ideal proteins are far more resistant to denaturation and more stable structurally. There are already principles and tools to do this.[16] At the moment you can create structures that mimic the capsid of viruses as drug delivery systems and could probably be the future of vaccines[14]
This opens the door to for a marriage between engineering and biology. To create human-made nanomachines with energy efficiency and speed never seen before. The consequences of motorized tools not reliant directly on internal combustion engines and electric motors could be sci-fi level changing.
One needs only to remember that a molecule of glucose moves inside the cell at 400km/h reaching it's target while competing with other molecules that also travel at that speed. At scale, it would be like coordinating cars that travel at 35 millions of kilometers per hour in the middle of crowded times square.[17],[18]The ATP synthase molecule of an E. coli spins at 42,000 rpm[19] Like this is not strange that enzymes collide 500.000/s with other molecules while propelled by motors that spin at 60 million rpm at scale.
Studying math has never been more important than now.
|
Protein Design: Nature's Math Origami
19 Comments


)