巧用初中知识解@kenchung的方程式数学题

偶尔去思考一下，避免自己迟钝下去。和我一起参加 @kenchung 的数学题，体会下思考的乐趣。希望大家多多支持 @kenchung 的数学X编程比赛，下一期即将开始。

传送门：[Question] Mathematics × Programming Competition #6 [問題] 數學 × 程式編寫比賽 (第六回)

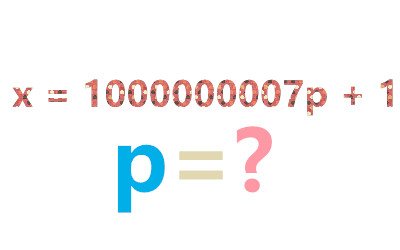
题目：已知 x 為平方數，而 p 為質數，且符合公式 x = 1000000007p + 1。求 p 所有可能值之和。

乍一看被这个大数字吓到了，肯定会有人想用编程解决，毫无疑问这道题用编程解决是非常的快，那么从数学的角度来解答呢？其实一样很简单。

x = 1000000007*p + 1 我们可以看作 x^2=1000000007*p + 1;

那么进行简单的变换下；

x^2-1=1000000007*p 即(x+1)*(x-1)=1000000007*p

到这儿我们可以看出来一个 1000000007*p是相隔2 的两个数相乘的结果。

1000000007*p 的因数为：p、1、1000000007

那么显而易见，p 要么是1000000009 要么是1000000005 ，或者0 ，因为p是质数，那么就只能是1000000009了

根据条件进行简单的构造，问题就迎刃而解了。

初中学习的x^2-1=(x+1)(x-1)还是挺好用的吗？有忘记吗？

除了数学比赛，还有 @armandocat 的 Coding challenge，传送门： Coding challenge #2 - Win SBD if you solve the problem!

Recent Posts