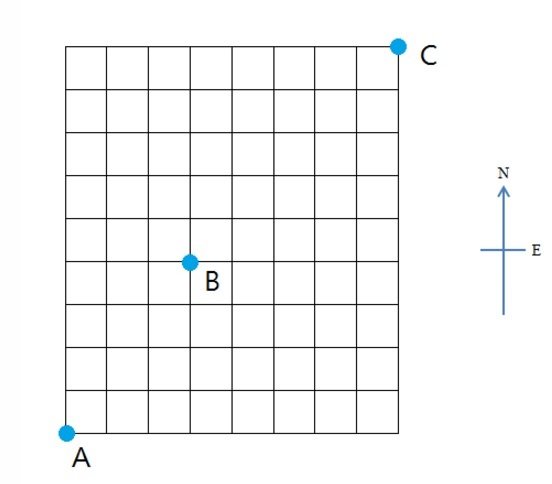
Let’s see this question: If @kenchung starts at A, and he can only travels one move at a time to the north or east, and he cannot go back. If he needs to travel through B, and finally reach C, how many ways are there for him to complete his journey?
有这么一题, 如果 @kenchung 从A到C, 一定要经过B, 并且每次走一步向东或者向北, 不能回头, 问一共有多少不同的方法.
BRUTE-FORCE? 暴力搜索(穷举)
In theory, you can write a program to count each possible path from A to C, then, only those paths through B are valid. This could take ages. For example, if A and B are separated by x steps horizontally and y steps vertically (x steps east and y steps north), the total number of paths is:
理论上说, 你可以用暴力列举所有从A到C的走法 然后再一一比较是否经过B, 不过这种方法很低效因为需要列举出所有走法. 如果水平有X步垂直有Y步那么一共的方案有:
 or
or 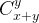
This reads: the number of ways to choose x or y items from (x + y) items. In this case, the x=8 and y=9, which makes the bruteforce inefficient.
可以这么理解, 一共有 x+y 步 选其中 x 或者 y 步来往东或者往北走.
PURE MATH SOLUTION 纯数学方法: 排列组合
A better way is to simplify the problem into two steps. First is to travel from A to B and the second step is to travel from B to C, thus, if we denote f(a, b) the number of paths from a to b, then the total number is:
细想一下, 我们只要分两个阶段即可: 第一个阶段计算由A到B的方法数, 第二个阶段计算由B到C的方法数, 然后这么一乘就是最后的方案数了.

So, you know the answer easily from the above.
根据本题, 最终方案为 .... (我知道你懂的)
RECURSION 递归
Let’s write a function f(x, y) which returns the number of different paths for x steps east and y steps north.
假设我们定义了 f(x, y) 用于计算 水平x步, 垂直y步的方案数: 那么:
function f($x, $y) {
if (($x == 0) || ($y == 0)) {
return 1;
}
return f($x - 1, $y) + f($x, $y - 1); // East of North, 1 step, two choices // 每次两种选择: 往东1步或者往北一步
}
And the answer is just: 最终答案就是:
echo f(3, 4) * f(5, 5);For each recursive call, there are two choices: 1 step north or 1 step east, so the answer is just to add these two (decompose into two smaller problems). The exiting conditions are when the offset is zero (step count is zero), this is when the answer should be returned as 1.
这里的递归写法可以认动态规化的一种, 退出条件就是当任意方向步长为0, 这时候就只有一种方案.
DYNAMIC PROGRAMMING (MEMORIZATION) 动态规化+记忆
The recursion is straightforward. However, it does not work well if the input is large, as a lot of intermediate results are computed again and again. You can memorize the intermediate results, which will speed up the computation (each f(x,y) is only computed once because next time the result will be fetched from memory):
递归的计算是很多冗余的, 因为很多中间计算在递归下去会被计算多次, 很低效. 这时候我们可以记录一下这些中间结果 这样速度就会快很多(每个 f(x,y) 值只会计算一次)
$cache = array();
function f($x, $y) {
global $cache;
if (($x == 0) || ($y == 0)) {
return 1;
}
$key = $x.' '.$y;
if (isset($cache[$key])) { // has the result been computed?
return $cache[$key];
}
$sol = f($x - 1, $y) + f($x, $y - 1);
$cache[$key] = $sol; // store the result
return $sol;
}
The next improvement to improve this Dynamic Programming DP implementation is to use the iteration, which avoids the recursion. This is computed bottom-up direction.
动态规化也不需要用递归来实现, 我们可以用更为高效的数组+迭代的方式, 从低往上计算.
function f($x, $y) {
$ans = array();
for ($i = 0; $i <= $x; ++ $i) $ans[$i][0] = 1;
for ($i = 0; $i <= $y; ++ $i) $ans[0][$i] = 1;
for ($i = 1; $i <= $x; ++ $i) {
for ($j = 1; $j <= $y; ++ $j) {
$ans[$i][$j] = $ans[$i - 1][$j] + $ans[$i][$j - 1];
}
}
return $ans[$x][$y];
}
This runs at complexity O(xy) as well as the space complexity (need to declare a 2-dimensional array).
时间复杂度和空间复杂度都是 O(xy). 为嘛用PHP? 因为PHP是世界上最好的语言.
Update: the next day, it comes to me that the space complexity can be further reduced to O(y): @justyy/software-engineer-interview-question-how-to-improve-dynamic-programming-space-complexity
更新:第二天 想到 空间复杂度可以降到 O(y): @justyy/software-engineer-interview-question-how-to-improve-dynamic-programming-space-complexity
PS: Why PHP? --- PHP is the best programming language in the world....

Originally published at https://steemit.com Thank you for reading my post, feel free to FOLLOW and Upvote @justyy which motivates me to create more quality posts.
原创首发于 https://steemit.com 非常感谢阅读, 欢迎FOLLOW和Upvote @justyy 能激励我创作更多更好的内容.
- Software Engineer Interview Question – How to Improve Dynamic Programming Space Complexity?
- 进一步改进动态规化的空间复杂度
- How many ways from A to C via B?
- 从A到B再到C有多少种方法?
近期热贴 Recent Popular Posts
- 24 Poker Game 24点扑克游戏
- Software Engineer Interview Question - Dynamic Programming - Integer Break 软件工程师面试技巧之 动态规化 - 整数拆分
- How to Claim BCC? BTC Hard-Fork via C program (Linux) 小白教程: 怎么领取 BCC (Bitcoin Cash) ?
- I wrote a Chinese Chess Program 软件分享: 智慧中国象棋 (Chinese Chess)
- Planning Cards – Agile Poker Game! 敏捷开发扑克游戏
- Software Engineer Interview Question - How to Check Valid Sudoku in C/C++? 软件工程师面试技巧之 如何检查数独的有效性
- Google Interview Question – Print Message - 去年 Google 的面试题 - 打印消息
- Software Engineer Interview Tips - Using Hashtable to Reduce Runtime Complexity 软件工程师面试技巧之 使用哈希表降复杂度
- Technology-driven or Business-model-driven? 技术优先还是商业模式优先 – 献给在30多岁还在写代码的朋友们
- 记录那些值得回忆的精彩瞬间
