#1 深度学习笔记 I – 卷积神经网络的直观解释 A - 整体结构
#2 深度学习笔记 II – 卷积神经网络的直观解释 B - Convolution & Pooling Step
#3 深度学习笔记 III – 卷积神经网络的直观解释 C - Introducing Non Linearity & Fully Connected
#4 深度学习笔记 IV – 多层感知器-前馈神经网络与反向传播学习 - Multi Layer Perceptron - Feedforward Neural Network&Backward Propagation of Errors
上一篇笔记中 @stabilowl在comment中对ReLU总结了一下,觉得总结得非常不错,记录在这里作为开篇,非常感谢。
我看了一下ReLu的资料,有几个有趣点:
1.ReLu也是从生物学借来的,因为神经元只有开和关,而不像sigmoid正反都有讯号。
2.Sigmoid 的斜率(slope) 永远小於0.25, 当神经网的深度变大,算backprop时所有sigmoid乘起来就会归零,所以sigmoid在深度学习基本上沒用。
3.当x小於0, ReLu的斜率等於0。若果一个神经元进入这个状态之后就只会归零。这个神经元就废了。所以用ReLu有可能算到一半整个神经网都废了(dying ReLu problem) 。这个问题可以用Leaky ReLu解决。
关于从生物学中借概念这一点,[1]这篇论文讲的很有意思,原来其实不止ReLU是从生物学借来的概念,另两个最早应用在神经网络中的激活函数:Logistic-Sigmoid与Tanh-Sigmoid被引入也是从生物学中借来的概念。这两个非线性的函数都是对中央区的信息增益大,但对两侧远端的信息增益小;在生物学里,中央区类比神经元的兴奋态,两侧区类比神经元的抑制态,因而在神经网络学习方面,可以将重点特征推向中央区,将非重点特征推向两侧远端区。下面图片里左边是一个真正的基于生物学数据建立的神经元的激活函数模型,右边是这两个激活函数。咦,从外形形状来看,貌似ReLU的函数图像更接近真正的生物学激活函数的模型?(跑题了,脑中时刻装着导师的谆谆教导,学工程的你管那么多底层细节干嘛)
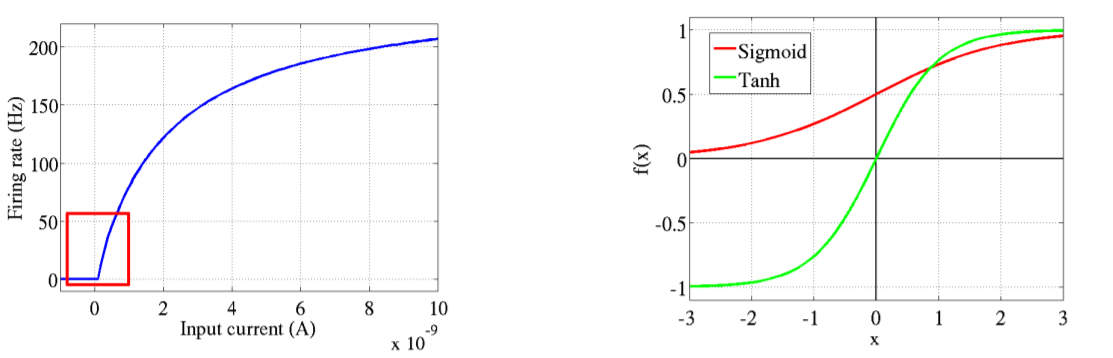
看看另外两个更接近真实的生物学中神经元激活概念的激活函数:Softplus和ReLu,其实Softplus可以看做是ReLU的平滑版本。
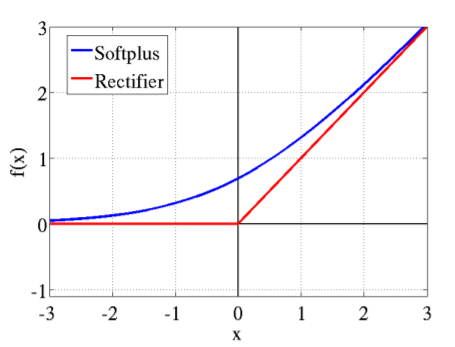
比起之前的两个激活函数,这辆激活函数带来了更大的优势:单侧抑制,可以看到左侧已经都被抑制了;更加宽的兴奋边界,右侧边界可以很宽;在激活稀疏性上完全匹配了生物学概念,大脑同时被激活的神经元只有4%左右,所以神经元工作具有稀疏性,图1左边的真实生物学激活函数中的开始也有一段未激活的区域,这个模型说明了神经元对输入信号作选择性响应,部分信号被刻意的屏蔽了,这样可以提高学习的精度,更好更快地提取稀疏特征(在神经网络中就减少了大量的计算);当然还有就是加快了计算速度。但是Softplus只照顾到了前两个优势,却没有在稀疏性上带来优势,所以ReLU成了最强王者。。。。
The rectifier activation function allows a network to easily obtain sparse representations. For example, after uniform initialization of the weights, around 50% of hidden units continuous output values are real zeros, and this fraction can easily increase with sparsity-inducing regularization. Apart from being more biologically plausible, sparsity also leads to mathematical advantages.[1]
当然肯定不是越稀疏越好了,下面图片是[1]经过实验得到的理想稀疏性比率是70%~85%,超过85%,导致错误率开始升高。
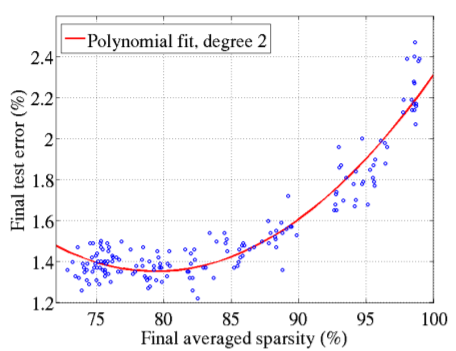
关于ReLU这个激活函数的中文文章倒是很多,关于这个知识点看来不用自己记录太多了,整理几个感觉自己读过以后对ReLu有进一步理解的。
1,起源:传统激活函数、脑神经元激活频率研究、稀疏激活性
2,为什么通常Relu比sigmoid和tanh强,有什么不同?
3,http://cs231n.github.io/neural-networks-1/
4,ReLU深度网络能逼近任意函数的原因
下一篇再记录一下反向传播算法,然后开始读相关论文干活,离deadline还有22天。。。。离CAFFE差得还有十万八千里
Reference
[1] Xavier Glorot, Antoine Bordes and Yoshua Bengio. Deep sparse rectifier neural networks
谢谢阅读 !
Thanks for your reading!
Please feel free to upvote, comment and follow me @victory622
