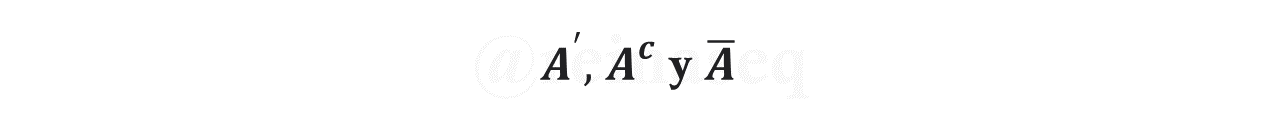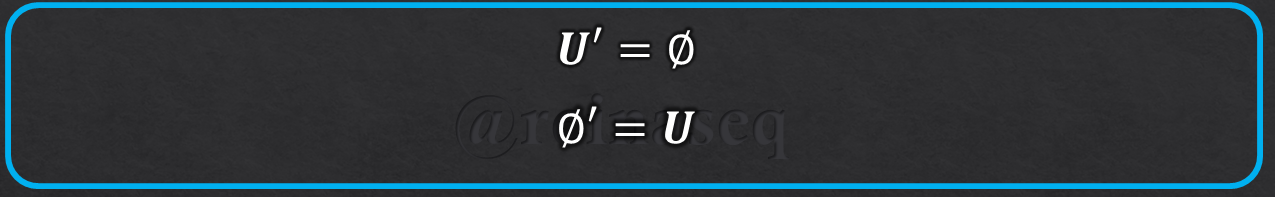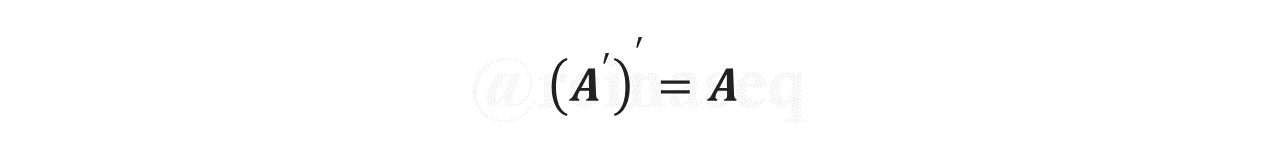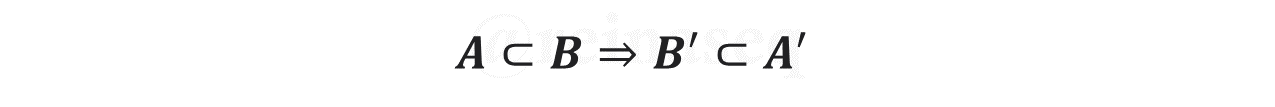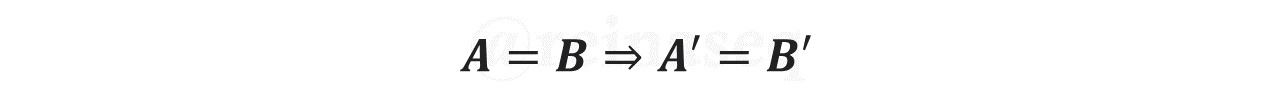Continuando con la temática referente a la Teoría de Conjuntos, específicamente a las operaciones, les presentaré a continuación otra de ellas de gran importancia en el ámbito de la Matemática, a saber, el Complemento de un Conjunto. Antes de entrar en la abstracción simbólica, es válido dar inicio preguntándonos desde la cotidianidad ¿qué pensamos cuando hablamos de complemento de algo?, seguramente muchos dirán cosas como: “es lo que le falta a ese algo”, “lo que necesita para ser completo”, “la parte que necesita para lograr la totalidad”. Y es que ciertamente, ninguna de esas posibles respuesta está errada en tanto que nada puede ser completo si le falta algo, en el escenario de la Matemática, específicamente cuando hablamos de conjuntos ser completo o ser total sería lograr ser el Conjunto Universal, de allí que se dice entonces que el complemento de un conjunto es todo lo que le falta para llegar a ser el universo.
Ahora bien, desde la formalidad algebraica el Complemento de un Conjunto se define de la siguiente manera: Dado un conjunto cualquiera A⊂U
Visualizando en un Diagrama de Venn
Como puede observarse en condición necesaria para que un elemento cualquiera pueda pertenecer al Complemento de un Conjunto que no pertenezca al conjunto en cuestión, esto nos lleva a concluir una de las características más resaltantes del mismo, se trata del hecho de que no existen elementos en común entre un conjunto y su complemento, es decir, son disjuntos (concepto que se ampliará cuando se estudie la Intersección de Conjunto). En la imagen puede apreciarse una de las notaciones más utilizadas, en general se acostumbran:
Así como es conveniente saber cuándo un elemento pertenece al Complemento de un Conjunto, es igualmente importante saber cuándo no pertenece y en este caso también se asume como definición del referido concepto. (ver en símbolos en la siguiente imagen). En líneas generales, se asume la en la definición que el Complemento de un Conjunto se determine en el Conjunto Universal, no obstante, también puede particularizarse la definición a la búsqueda del complemento de un conjunto en otro conjunto cualquiera B⊂U, esto puede ser visualizado en símbolos en la siguiente imagen:
Como afirmaciones obvias y de sencilla deducción basados en la definición precedente se desprenden que el complemento del Conjunto Universal es el Conjunto Vacío y a su vez el complemento del Conjunto Vacío es el Conjunto Universal, lo cual se expresa en símbolos como sigue
Propiedades del Complemento de un Conjunto
- Involución: El complemento del complemento de un conjunto es igual al conjunto. En símbolos
Para demostrar esta propiedad debemos observar algunas precisiones: en primer lugar se trata de una Igualdad de Conjuntos, por lo cual debe demostrarse la doble inclusión tal como expliqué en mi publicación anterior. Por otro lado, se deben tener presente la definición de Complemento de un Conjunto tanto para la pertenencia como para la no pertenencia a dicho conjunto. Dicho esto, procedamos con la demostración.
- Si un conjunto es subconjunto de un segundo, entonces el complemento del segundo esta incluido en el complemento del primero
Demostrar esta propiedad requiere tener presentes las definiciones de Inclusión de Conjuntos y de Complemento de un Conjunto, además de considerar la hipótesis dada A⊂B . Procedamos:
Ejercicio: Demostrar que si
Para llevar a cabo la siguiente demostración debemos observar lo siguiente: en primer lugar se trata de una implicación, eso quiere decir que lo que se encuentra a la izquierda de ella se debe considerar como la hipótesis y servirá de ayuda en algún momento del proceso demostrativo, y lo que está a la derecha es la tesis, por tanto es lo que se debe comprobar. Al observar la tesis nos damos cuenta de que se trata de una Igualdad de Conjuntos eso quiere decir que se debe demostrar la doble inclusión. Adicionalmente se debe tener presente la definición del complemento de un conjunto. Realizado el análisis previo, procedamos con la demostración.
Nos leemos en las próximas publicaciones en las cuales seguiré con la temática de Operaciones con Conjuntos.

Las matemáticas puras son, en su forma, la poesía de las ideas lógicas - Albert Einstein.

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Todas las imágenes, separadores y banners de este artículo son de autoría propia.
Artículo Anterior