One of the most fundamental symmetry of nature, the CPT symmetry, is trying to be falsified for years by high-energy physicists. And today… it is still valid!
In this post, I will discuss the C, P and T transformations, and the definition of the resulting CPT symmetry and why we are trying to falsify it.
Antimatter experiments are very exciting as they aim to measure the properties of the antimatter particles, and thus verify that the observations match those of the corresponding matter particles (up to sometimes a global minus sign). This consists of a deep test of the CPT theorem, one of the most fundamental symmetries of nature.
I will not speak about the news of last December, where the antihydrogen energy spectrum was precisely measured at CERN by the ALPHA experiment (see here for the official announcement]). The reason is that this is an old news that has been widely covered on Steemit by at least three authors (I may have forgotten some, apologies in advance and please let me know in the comments): @dragosroua (see here), @krnel (see here), and @daianynascimento (see here).

[image credits: CERN]
I will instead move on with recent BASE measurements and use them as a good excuse to write in details on the CPT symmetry.
ELEMENTARY PARTICLES AND ANTIPARTICLES
[image credits: CERN]
Before starting, I will recap a few things about the concepts of elementary particles and antiparticles.
In a very old post of mine, written at the time I just joined Steemit, I have browsed the landscape of the Standard Model of particle physics, describing the elementary particles that are the building blocks of nature and the way they interact with each other through three out of the four fundamental forces. Moreover, for details on the Higgs boson (although this is not related to what I will talk about today), see my two posts on the topic here and there).
Each of these particles is always associated with an antiparticle. We hence have quarks and antiquarks, electrons and positrons, muons and antimuons, and so on. But what are the differences between a particle and an antiparticle?
They are actually very few differences. Particle physics relies on quantum field theory, where the basic objects are quantum fields. A particle and a corresponding antiparticle can be seen as excitations of a given field. Skipping all nasty details, the important point is that particles and antiparticles are connected to the same object. Which means, they must have similar properties and exhibit very few differences.
THE CPT SYMMETRY AND PARTICLE PHYSICS MODEL BUILDING
And what I said in the above section is exactly what is going on. Particles and antiparticles are entities that have very few differences.
They are characterized by their mass, their width (or give or take, their lifetime), and their electric charge (or any other quantum number if we want to use nice words and be precise). Moreover, if we compare all the properties of a given particle and the corresponding antiparticle, they will be the same up to the quantum numbers that will be opposite. A particle and an antiparticle will have an opposite electric charge, for instance.
In addition (and now this is actually the important point), when we build the way particles and antiparticles will interact, we actually design a mathematical function of the various fields of the model. This function (also known as a Lagrangian to use another nice word) embeds how every single particle will interact with any other particles.
This function is however not random, and there are constraints on how it should be constructed. The Lagrangian must satisfy some symmetries. This ranges from the symmetries connected to the fundamental interactions to the famous CPT symmetry. I will focus on the latter, the CPT symmetry.
The CPT symmetry is an acronym standing for charge, parity and time-reversal symmetry. What does it mean? Let us consider a given reaction involving a bunch of particles.
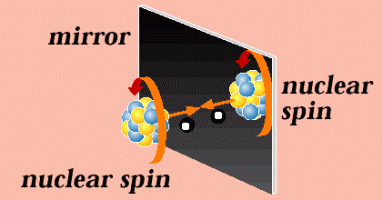
[image credits: LBL]
The P transformation means that the spatial configuration of the particles is reversed. It can be seen as a mirror transformation: we put the reaction in front of a mirror so that everything is flipped (left becomes right, for instance). I illustrate this one with the image on the right for clarity.
The C transformation makes all particles replaced by antiparticles.
The T transformation acts on the time that is made running backwards instead of forward.
There are fundamental reasons that nature is CPT symmetric, or that the laws of nature are equivalently invariant under a joint C, P and T transformation. This can be demonstrated within the quantum fied theory framework.
THE INDIVIDUAL C, P AND T SYMMETRIES
We mention the CPT symmetry, but one may ask to ourselves, why not having P, C or T conserved individually and being good symmetries of nature? Because of data! There exist concrete examples showing that the three individual transformations are not symmetries of nature. This was actually not always believed to be like that.
A beta decay is not invariant under a P transformation, as observed in 1957 by C.S. Wu and collaborators. The electrons arising from such a decay have a preferred direction opposite to the spin projection. In the case of a P symmetry, one would observe both the reaction and its mirror image equally. This is not the case.
From then, physicists were believing that CP was a correct symmetry of nature. C and P were thought to be both violated, but the two violations were canceling each other. But what is a CP transformation more precisely?
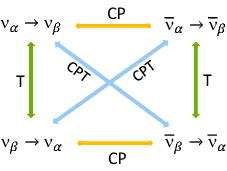
[image credits: CERN]
Let us take an electron moving with a velocity v. Through a mirror transformation, we get an electron moving with a velocity -v. Then, if we replace an electron by a positron (the C transformation), we get a positron moving with a velocity -v. This means that a CP transformation gives us the mirror image of the associated antimatter particle. This is illustrated in the picture on the left by the horizontal lines.
In 1964, V. Fitch and J. Cronin (and collaborators) observed that the CP symmetry was violated in the decays of some particles called kaons. The CP transformation is thus not a symmetry of nature, as T (since CPT cannot be violated). The amount of CP violation is thus compensated by the amount of T violation. And all of this is fully accommodated in the Standard Model.
FALSIFYING THE CPT SYMMETRY - THE BASE EXPERIMENT

[image credits: CERN]
Since the CPT symmetry seems to be a symmetry of nature, physicists are trying to falsify it for decades. Equivalently, this means to verify this assumption to the deepest level.
The BASE collaboration at CERN is aiming to measure the magnetic moment of the antiproton, and a comparison with proton data will provide a sensitive test of the CPT invariance.
Just for fun, ‘BASE’ is an acronym standing for the Baryon Antibaryon Symmetry Experiment.
BASE has reported last week the most precise measurement ever made of the antiproton magnetic moment. It has been shown that the proton and antiproton moments are identical, apart from their opposite signs, within an error of 0.8 parts in a million. That is precision! This sign difference is exactly the only difference predicted by the CPT symmetry.
To make a long story short, the BASE experiment uses the slowed down (and cooled down) antiprotons produced at CERN. It then studies their behavior within a magnetic field, once antiprotons are trapped within a magnetic container.
The next step is to improve the precision by a factor of 200 to 800 in a rather close future, thanks to a new antiproton trapping technique.
SUMMARY
In this post, I detailed what is the CPT fundamental symmetry of nature, and also what the C, P and T transformations meant. This brought me to touch the concept of matter and antimatter and the tests physicists are making to unravel matter-antimatter difference.
The BASE experiment is one of the experiments that are trying to falsify the CPT invariance of nature. It relies on measuring the antiproton magnetic moment with an extreme precision, and to compare the results with the proton data.
For the moment, nothing seems to show that the CPT symmetry does not hold.
