In my previous post on the physics beyond the Standard Model of particle physics, I presented few motivations for this very active field of research. At the end of the post, I offered to describe the most popular paradigms that are considered for new physics studies, and here we are.
[image credits: particle central]
Supersymmetry is the class of models which I focused on when I entered the field of particle physics. Very popular at that time, supersymmetry, also abbreviated as SUSY, is still in the pipeline. It is even at the basis of a very important fraction of the experimental searches for new phenomena.
Although supersymmetric signals are expected to show up at the energies probed at the Large Hadron Collider at CERN, nothing has been found so far. Nevertheless, supersymmetric theories have a very rich phenomenology and are thus widely accepted as at least playgrounds to test new physics.
FROM THE FUNDAMENTAL INTERACTIONS TO SYMMETRIES
Before discussing anything related to supersymmetry, it is important to emphasize that we have two classes of particles in nature, that differ according to their spin (an intrinsic property of each particle).
We have particles whose spin is integer, known as bosons (like the Higgs boson, the photon or the gluon) and particles with a half-integer spin, known as fermions (like all elementary matter constituents such as the electron, the quark or the muon). Both have very different properties.

[image credits: homemade]
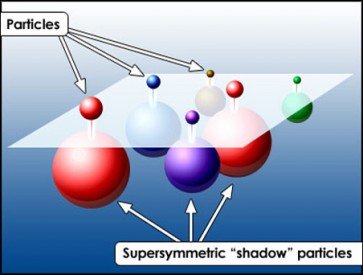
The word supersymmetry contains the word symmetry, and this is not a random choice. Supersymmetry is in fact one possible symmetry of nature. The particularity of supersymmetry is that it is a symmetry that connects bosons and fermions.
This type of symmetry changes the bosonic/fermionic nature of the particles and thus generalizes the usual way symmetries are seen. A supersymmetry transforms a boson into a fermion, and vice versa. Moreover, particles mapped by a supersymmetry should have similar properties (mass, charge, etc). This has profound consequences.
THE SIMPLEST SUPERSYMMETRIC MODEL AND THE SUPERPARTNERS
[image credits: CERN (but cannot find where anymore)]
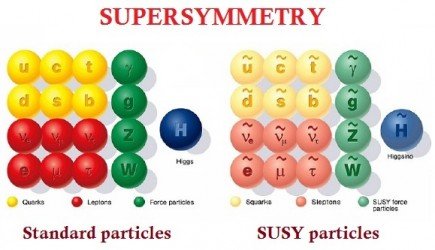
The simplest theory we could try to build is a supersymmetric version of the Standard Model. As said above, supersymmetry transforms a boson into a fermion and vice versa. We however do not have enough particles to allow supersymmetry to work within the Standard Model particles.
In particular as they are some requirements on the common properties of the particles connected by a supersymmetry. The solution is simple: let us add as many new particles as required for supersymmetry to be a symmetry of nature.
Each particle of the Standard Model has now a partner, or a superpartner, connected by a supersymmetry operation. We have hence electrons and selectrons, quarks and squarks, photons and photinos, Higgs bosons and higgsinos, etc. A lot of cool names, and a lot of potential particles to discover.
But can nature be supersymmetric? By symmetry reasons, a Standard Model particle and its superpartner should have the same mass so that the superpartners should have already be observed.
As this is not the case, we must construct a model by enforcing supersymmetry in a first step, but then we break it spontaneously to introduce mass splittings between the Standard Model particles and their partners. I refer to this post of mine for more information on the symmetry breaking mechanism.
Symmetry breaking is standard, so no big deal here :)
CURING THE ISSUES OF THE STANDARD MODEL

[image credits: pixabay]
Nature does not necessarily need to be supersymmetric, but it could be. And if it is, we have a natural solution to many of the issues that I have mentioned in my previous post. This makes supersymmetry attractive as an option for describing what we do not know about nature and get below the Standard Model iceberg.
First of all, by construction, supersymmetry unifies the concept of bosons and fermions with the fundamental interactions. We have symmetries explaining the strong, weak and electromagnetic interactions, as well as symmetries mapping the Standard Model bosons to their superpartners.
In my last post, I mentioned the hierarchy problem implying that the Higgs boson mass was very sensitive to the quantum corrections except if the model parameters were tuned to their 30th decimal. In supersymmetry, this is not needed anymore. The effects of the superpartners exactly cancel those of the Standard Model, and the Higgs mass thus behaves nicely, provided the supersymmetric guys are not too heavy. This is why we expect them to show up at the LHC.
On top of that, the lightest superpartner has in general an interesting property. It can be made neutral, weakly interacting and stable. These are exactly the properties of a particle that could play the role of the dark matter. Bingo! Supersymmetry can explain dark matter.
The presence of the superpartners also modifies the dependence of the fundamental interaction strengths with the energy. And as a result, the three fundamental interaction couplings unify at a scale roughly lying three orders of magnitude below the Planck mass scale. We have now an energy regime where three of the fundamental forces can potentially unify.
There are many other advantages for a supersymmetric theory but I will try to prevent this post from exploding in length. So that I stop here.
OBSERVING SUPERSYMMETRY?
[image credits: CERN]
I have so far described the gains associated with imposing a theory to be supersymmetric. But the next step would be to detect the consequences of such.
Since the superpartners are sensitive to the fundamental interactions in the same way as their Standard Model counterparts (supersymmetry is a symmetry after all), they can be produced at colliders such as the LHC and thus searched for.
These superparticles are however unstable and will decay. A superpartner always (OK not always but let us keep the scenario dark-matter motivated) decays into another superpartner and a Standard Model particle. But the lightest superpartner cannot decay and is stable. A particle can indeed only decay into a lighter particle and there is none available for the lightest superpartner.
Freshly produced superpartners will then decay into each other, forming a nice cascade, until the lightest one, stable and weakly interacting, will leave the detectors invisibly. These cascade decays can be observed, including the missing energy carried by the escaping lightest superpartners, and they are thus actively searched for. However, unfortunately, there is no signal so far.
SUMMARY
With this first post trying to give elements about the numerous theories of particle physics beyond the Standard Model, I have introduced the concept of supersymmetry, a symmetry connecting bosons with fermions. As a result of this connection, each Standard Model particle gets a superpartner, a particle with the same properties but a different bosonic/fermionic nature.
Whilst doubling the number of particles may sound complicated, this allows one to address many of the conceptual issues of the Standard Model, like the hierarchy problem, the dark matter issue or the unification of the fundamental interactions.
In the next episode, I will discuss a former competitor to supersymmetry in terms of popularity, extra-dimensional models. They are still considered today, but not as much as 10 years ago.
