Weak interactions play a crucial role on the structure of the universe and everything that lies into it. This motivated me to write about it in this post.
[image credits: wikipedia]
As I have mentioned in many other posts, the weak force is one of the four fundamental forces of nature, with electromagnetism, gravity and the strong interactions.
I will dedicate this post to the discovery of this force and how it has been theoretically modeled over time.
FUNDAMENTAL INTERACTIONS IN THE MICROSCOPIC WORLD
I start by summarizing a little bit the properties of the fundamental interactions. More detailed information can be found in these two older posts of mine, here and there.

[image credits: Discover Magazine]
Although there are many different type of interactions at the macroscopic level (i.e. in everyday life), there are only four different interactions at the level of the fundamental constituents of matters.
Out of these four forces, gravity does not play any role. The strength of the gravitational interaction is proportional to the mass of the interacting bodies, and elementary particle masses are so tiny that the net effect is just negligible.
We are thus left with electromagnetism and the weak and strong interactions.

[image credits: Science Kids]
Electromagnetism is very well known as it is the second fundamental interaction that has been discovered, thanks in particular to its infinite range (although electromagnetic are mostly screened in everyday life since matter is mostly electrically neutral).
This force is crucial as it plays one of the leading role in explaining the structure of matter, describing how electrons and atomic nuclei interact.


[image credits: Fermilab, Nobel Prize]
The range of the strong and weak interactions being much smaller, these forces have been discovered way later, through the study of radioactivity. The strong interactions are important to explain the structure of the atomic nuclei and how nucleons (i.e., protons and neutrons) are made of elementary quarks and gluons.
I will focus on this post on the last of these forces, the weak force.
THE WEAK FORCE IN A NUTSHELL
The weak force is a force that is 100.000 times weaker than the strong interaction, and has no impact on the structure of matter. This contrasts with electromagnetism and the strong interactions.
The role of this force is to allow some particles to decay into each other, but in a kind of slow fashion. For instance, the weak force enables beta decays where one particle species transforms into another type of particles, this process being accompanied with the emission of other (lighter) particles.
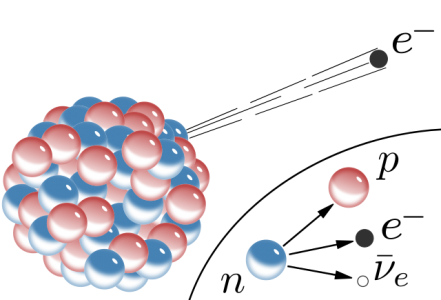
For instance, a neutron could transform into a lighter proton, or decay into a proton via beta decays. More precisely, the neutron decays into a proton, an electron and a neutrino as in,
n → p e— νe
The above process is rendered possible through weak interactions, and it has in some sense played a key role in the theoretical modeling of the weak interactions.
Beta decays have very important consequences. For instance, the sun burns slowly through weak interactions, so that life had the time to develop on Earth (and this is a good thing!).
As another very important consequence of the beta decays, we can quote the diversity of the chemical elements in the universe that is due to the weak interactions. The heavier elements are indeed formed through beta decays in stars.
FROM HAHN AND MEITNER TO PAULI AND THE NEUTRINO
All of this started with a problem that appeared in 1911. Hahn and Meitner were studying the decays of atomic nuclei into other nuclei. As nuclei are made of protons and neutrons, this was actually a way to study neutron decays into protons, i.e. the reaction shown above. However, imagine there were no neutrons at that time. And no neutrinos too (and no John Lennon).
The reaction that has been considered by Hahn and Neitner is in fact
A → B e—
where A and B denote two atomic nuclei (A being heavier than B).
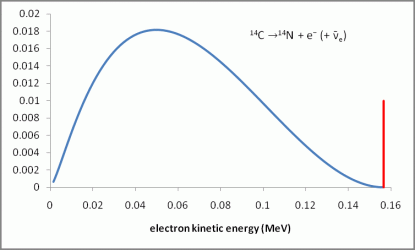
Hahn and Meitner were investigating the properties of the electron present in the final state of the above reaction, comparing data to theoretical predictions. If one uses energy-momentum conservation, one can calculate the energy of the final-state electron.
This value is well-defined and unique and is given by the energy difference between the initial-state and final-state nuclei.
[image credits: the T2K experiment]
This is not what was observed. Plenty of values were actually measured, and one ended up with a fully non-trivial electron energy spectrum, contradicting the predictions.
This is illustrated on the left picture for carbon decays into nitrogen. The red bar is what is expected from energy-momentum conservation. The blue spectrum is what would be observed in an experiment.
As this was not in agreement energy-momentum conservation and as energy-momentum conservation is a concept very hard to abandon (it is satisfied everywhere), something new was in there.
Pauli proposed an explanation 20 years later. He suggested that a third particle was present in the final state, an invisible guy, so that the energy could be shared between the electron and this particle. The actual reaction that was happening was thus
A → B e— νe
In order to match the observations, the properties of this new particle cannot be random: it has to be very light and feebly interacting. That is how the neutrino was postulated for the first time (although the name came later).
CHADWICK, FERMI AND THE FERMI THEORY
This was the observational status at the beginning of the 1930ies, but physicists had still to build the underlying theory. The first step in that direction was… experimental. Chadwick discovered the neutron in 1932, so that Fermi could develop the idea of Pauli further.
[image credits: homemade]
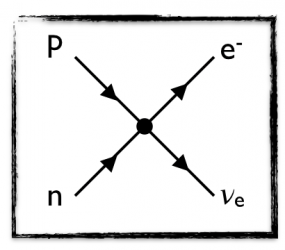
Nuclei were made of neutrons and protons, and the reaction that was occurring during a beta decay was in fact a reaction involving the transformation of a heavier neutron into a lighter proton, as already mentioned,
n → p e— νe
Fermi modeled the above reaction as occurring through a four-point interaction, or a contact interaction involving four particles. The exact form of this contact interaction illustrated in the Feynman diagram on the right was constrained by data, but it has in fact changed over time due to various options, discussions and data.
More precisely, Fermi initially proposed something, but other options were equally possible theoretically, and the only way to know which one was right was to check with the observations.

[image credits: Wikipedia]
The key year was 1956 when Lee and Yang pointed out that there were no proof that the weak interactions were conserving a symmetry called parity (more information on parity is given in this post). Wu and her collaborators jumped on that and experimentally demonstrated that parity was not conserved in the weak interactions thanks to the apparatus shown on the left.
This extended the initial modeling by Fermi and others (that was parity-conserving) with a more complicated structure, and extra parameters entered into the game. A plethora of experiments happened in 1957-1958 to constrain those extra parameters, and data favored at the end of the day the so-called V-A structure of the weak interactions proposed by Marshak/Sudarshan and Feynman/Gell-Mann.
The V-A theory was extremely successful, with a phenomenology in agreement with every single experiment designed in the years following its conception.
But it could not be the end of the story.
TOWARDS THE GLASHOW-SALAM-WEINBERG THEORY
The problem of the Fermi theory, or the V-A theory, is very simple.
This theory can be used to calculate predictions of weak interacting processes, both decay and production processes. We can in particular make use of the theory to calculate the rate of producing some particles via weak interactions.
This rate is found to grow with the energy. But quantum field theory does not allow for an infinite growth, so that the V-A theory is expected to break down at some high energy.
It is thus clear that the theory is incomplete.
[image credits: homemade]
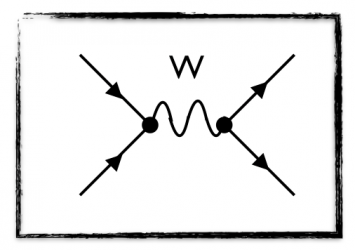
The solution comes originally from Yukawa who suggested it long ago, but it was concretized by Glashow, Salam and Weinberg in 1968.
They rewrote the four-point interaction of Fermi as an exchange of a heavy particle, a weak boson mediating the weak interactions. This is simply the W-boson discovered in 1983 at CERN, and the theory consists of a gauge theory for weak interactions.
If the energy of the process is small, the weak-boson exchange looks like a four-point interaction. If the energy of the process is large, the four-point interaction modeling breaks down, and only the weak boson exchange must be considered for actual calculations.
There is however another weak boson, the Z-boson, but how it arises will be the topic of another article (this one is already long enough) :)
SUMMARY
In this article, I detailed how the theory of the weak interactions was born. I started with existing issues in describing the decays of atomic nuclei 100 years ago, and detailed how it had triggered an intense theoretical activity.
Several big names of physics tried to tackle this problem very hardly, before one ended up with a satisfactory theory. The first attempt was the Fermi theory, that has been replaced with a gauge theory for the weak interactions (that agrees with all data).
I have however not told the entire story, as we are today talking about electroweak interactions which I have not mentioned so far. This will be for a future post.
For further pieces of information, do not hesitate to read:
- Veltman's book: it is a good approach for anyone not yet in the field;
- Peskin and Schroeder: the bible used in many universities as the reference
