
This post is the third one of my Steemit project of sharing quantum mechanics lecture notes. In the previous posts, I have so far introduced the basic interactions, particle species and conservation laws necessary to detail quantum mechanics. However, this theory also describes composite systems made of elementary building blocks.
This is the topic of this post, that is also the last post of the introduction chapter of my lecture notes.
The previous posts can be found by following these links:
I will now show how elementary particles are combined to form composite systems that can be studied with the help of quantum mechanics.
THE GOAL BEHIND QUANTUM MECHANICS (TABLE OF CONTENT)
Quantum mechanics (and its generalizations) is a theory suitable to study systems of particles. A given system is made of simpler building blocks that can be either elementary particles or simpler composite systems.
A system of particles has always a given size or energy scale, and a specific fundamental interaction is responsible for gluing the system constituents together.
The four types of systems I will be interested by are:
The nucleons (or equivalently the protons and the neutrons) already discussed in my previous post. They are systems made of quarks and gluons that are bound together by virtue of the strong interactions. The nucleon size is slightly less that 1 fm (or 10-15 m).
The atomic nuclei that are systems made of protons and neutrons (or nucleons). Neutrons and protons form nuclei by virtue of the strong interactions and an atomic nucleus as a size of 1 to 10 fm.
At a large size level, atomic nuclei and electrons form well-known system called atoms. The interactions responsible for this are the electromagnetic interactions (the range of the strong interaction is actually too small to be relevant here) and we are dealing with large system of 0.05 to 0.5 nm (or 5 to 50 ×10−11 m).
Finally, quantum mechanics can also be used to describe molecules that are systems made of atoms bound together through electromagnetic interactions. Their size is very large, way above 10 nm.
Atoms and molecules have also be largely described in the chemistry lessons designed by @justtryme90 (that actually focus more on the interactions of the molecules all together).
THE STANDARD MODEL OF PARTICLE PHYSICS IN FOUR PARAGRAPHS

[image credits: The Particle Adventure]
I will not discuss in detail the Standard Model of particle physics as this has been already done extensively in one of my first posts on Steemit.
Instead, it is good to mention that the Standard Model requires a generalisation of the quantum mechanics material that I am designing here that includes relativistic effects.
In a few words, to make this post self-consistent, the Standard Model describes the world of the elementary particles and their interactions.
Quarks and gluons are objects whose dynamics is described by the Standard Model. The latter also details how they can form composite objects called nucleons through quantum chromodynamics (and its property of confinement).
The Standard Model additionally includes leptons like the electron and the associated neutrino. Other leptons (muons, taus and the corresponding neutrinos) exist, and can be considered as heavier versions of the electron and the electronic neutrino (which is barely true for the neutrino but let us forget about this).
I will not say more about the Standard Model (please check my older post for more information), and not even mention the fact that the fundamental interactions are mediated by another species of elementary particles, the gauge bosons and that a Higgs boson is necessary for incorporating the particle masses in the theory. Well okay I said it anyhow...
For the Higgs boson, I can also refer to two older posts I wrote on its theoretical and experimental aspects.
NUCLEONS
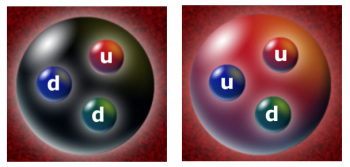
[image credits unknown (everywhere on the web)]
I have already widely discussed nucleons in my previous quantum mechanics post so that I will only present a short summary here, again, with the aim of making this post self-consistent.
Neutrons and protons (the two versions of the nucleon) are not elementary particles and are made of quarks and gluons. The nucleon constituents are bound together by virtue of the strong interactions and they can naively be seen as systems of three quarks. The reality is more complex.
The dynamics of the nucleons is described by a theory named quantum chromodynamics confirmed experimentally by more than 50 years of data. This makes the structure of the nucleons highly complex because of continuous phenomena of gluon exchanges by quarks and other gluons and of quark-antiquark pair creations and annihilations.
It is consequently tremendously complicated to deduce the nucleon mass from the one of its constituents. This is actually the field of lattice quantum chromodynamics, a very active field of research.
ATOMIC NUCLEI
[image credits unknown (everywhere on the web)]
An atomic nucleus is a system made of protons and neutrons. It is in fact made of elementary quarks and gluons, but the complexity of quantum chromodynamics render any associated calculations impossible. Taking care of the limit calculation allowing us to connect particle physics to nuclear physics is presently not feasible.
This is why nuclear physics is based on computations involving nucleons as basic objects, and not their constituents. Moreover, the form of the interactions between two nucleons is not exactly known and tuning is made from data.
Let us take an element X containing Z protons and N neutrons. Its charge is Ze with Z being called the atomic number. For practical reason, we also introduce the total number of nucleons inside the nucleus A = Z + N.
The element above is usually noted as AX. For instance, 1H is an hydrogen nucleus a 2H is a deuteron. While the hydrogen nucleus is nothing but the proton, the deuteron is an hydrogen stable isotope with a nucleus made of one proton and one neutron.
The mass of a nucleus m is not exactly equal to the sum of the masses of its constituents and turns out to be 0.8% lighter. We indeed need to subtract the binding energy B,
- m = N mn + Z mp - B/c2
where mn is the neutron mass, mp the proton mass and c the speed of light. The binding energy is usually of a couple of MeV (mega-electron-Volts), with
- 1 MeV = 1.602177 × 10−13 J.
Finally, moving on with the size of a nucleus, the latter is approximated given by
- R = r0 A1/3
with r0 = 1.24 fm.
There are 275 stable nuclei (that cannot decay into lighter nuclei or that have a lifetime much larger than the age of the universe) and they all have Z smaller than 83. It is important to recall that instable nuclei may exist on Earth (like 238U that has a lifetime close to the age of Earth).
ATOMS
It is now time to introduce atoms that are made of one atomic nucleus and one or many electrons orbiting around it.
In atomic physics, the nucleus is considered as a single heavy particle and there are Z electrons where Z is once again the nucleus atomic number. An atom is thus neutral, which contrasts with charged ions where the number of electrons is different from Z so that the positive electric charge of the nucleus is not exactly compensated.
In an atom, particles (i.e. the nucleus and the electrons) interact via electromagnetic interactions and the atomic mass M is approximatively given by the mass of its nucleus** since the electron mass and the binding energy are much smaller. More precisely, we have
- M = m + Z me - Be/c2
where me is the electron mass and Be the electron binding energy that is usually of the order of a few eV. The approximation M=m holds in general at the permile level.
Finally, to repeat what has been said in the beginning of this post, the atomic sizes range from 50 to 500 fm.
MOLECULES
[image credits: pixabay]
Molecules that are arrangements of several atoms and are thus systems made of several nuclei and electrons.
Molecules can be electrically neutral or charged (we are then talking of a molecular ion) and the number of atoms can range from 2 (the neutral H2 molecule and the molecular ion H2+) to thousands like in various organic systems.
Molecule masses are very close to the sum of the mass of their constituting atoms (the binding energy is extremely small) and their size vary a lot, from the atomic size for the smallest molecules to a huge number for large organic molecules.
SUMMARY
In this third post on quantum mechanics, I have introduced various composite systems that we will try to describe by means of the laws of the quantum world. In particule, the hydrogen atom is on of the key players. But this is the topic of the next posts. Here, I only focused on a quick description of all systems of interest.
In my next post, I will start the second chapter of these lectures and I will discuss the origins of quantum mechanics.
For any question or further pieces of information, do not hesitate to comment or pass by the #steemSTEM channel o the Steemit chat.
