
In my previous article, I highlighted and explained one of the greatest mysteries in physics of the end of the 19th century and beginning of the 20th century: the understanding of the atomic spectra.
But this was not the only problem physicists were trying to solve. Specific macroscopic systems, named black bodies, were scrutinized and their understanding was a problem in the light of classical physics. A funny fact is that the Planck constant, that is the fundamental constant associated with quantum mechanics and the microscopic world, finds its original in the study of those macroscopic black bodies.
This consists of the topic of this article. I will first detail what is exactly a black body, before moving on with the associated problems and the solutions that have been proposed.
This will finally lead me to Max Planck, his constant (that is one of the universal constants of physics) and his proposal for quantizing the energy.
BLACK BODIES
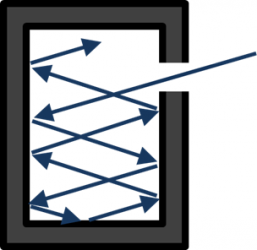
[image credits: Wikipedia]
A black body, as illustrated on the picture on the left, is a system with a fixed temperature, in thermodynamical equilibrium and that absorbs every single radiation, no matter is the wavelength of the radiation is. The key parameter is the black-body temperature T.
A black body can roughly be seen as a cavity with a hole so that radiation can come in but not go out. The entry point is small enough for the equilibrium the be maintained, but large enough to allow us for observing the phenomena occurring inside.
In the every-day-life world, many objects can be approximated by black bodies. For instance, the radiation pattern of a star (including our sun) is a black body radiation pattern.
Furthermore, the most famous natural black body system is the cosmic microwave background which is visible everywhere in our universe. This corresponds to a black body of temperature of about T=3 K (K means Kelvin degrees). This originates from the recombination era in the universe history where atoms have been formed. This is however not the topic of this article, and I refer to my older post on standard cosmology and the history of the universe for more information.
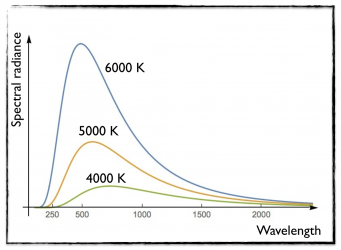
[image credits: mine]
A black body system acutally not only absorbs radiation, but also radiates. Although this emission spans all possible frequencies, the radiation pattern is not uniform. The radiation intensity depends on the radiation wavelength, and exhibits a maximum whose position depends on the temperature.
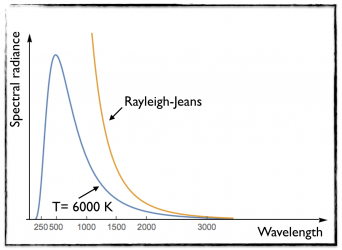
This is illustrated in the picture on the right, where the black-body spectral radiance is presented as a function of the wavelength. The spectral radiance is roughly the amount of energy emitted by the black body when it radiates at a given wavelength.
In this curve, I consider three black bodies with temperatures of 4000, 5000 and 6000 K, whose spectra radiances are respectively presented in green, orange and blue. The maximum is not necessarily in the visible domain.
WIEN’S DISPLACEMENT LAW
Before 1900, physicists were not capable to explain the spectral radiance distribution of a black body. Several very well-known physicists have however tried hard.
For instance, Wilhelm Wien has established, in 1893, a law that carries his name. Yep, physicists (and scientists in general) are not that good in finding names…
Using general thermodynamics arguments, Wien managed to derive the following general equation,
u(ν,T) = ν3 f(ν/T)
The internal energy density (u) of a black body depends on the radiation frequency (ν) and the temperature (T) on a very well-defined manner. It is proportional to the third power of the frequency times a function of the ratio ν/T. The form of the function has was to be determined.
Just a small reminder: the radiation frequency is inversely proportional to the radiation wavelength.
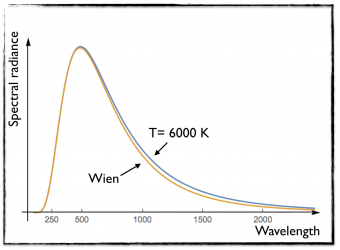
[image credits: mine]
A few years later, Wien used high frequency black body data to fit the function f. He got
uW(ν,T) = α ν3 exp(- γ ν/T)
with two parameters α and γ to be adjusted from data. The W index recalls that this relation is the relation found by Wien.
While this law was working quit well for small wavelength (or large frequencies), it was drastically failing to match the black-body behavior at low frequency (or at large wavelength). This is illustrated in the figure on the left, where I took a black body of temperature T= 6000 K.
The orange curve (obtained from Wien’s law) differs from the blue curve (black body data) at large wavelengths.
THE RAYLEIGH-JEANS LAW
In 1900, John Rayleigh and James Jeans used classical statistical physics to get another form for the internal energy density of a black-body,
uRJ(ν,T) = (ν/c)2 1/c E(T) = (ν/c)3 8 π kB (T/ν)
where the subscript RJ recalls that this is the relation derived by Rayleigh and Jeans.
This agrees with the general form of u(ν,T) derived by Wien above, but for a different function f. We recall that the kB parameter is the Boltzmann constant equal to 1.380649 × 10−23 J/K.
Rayleigh and Jeans started to determine the number of vibration modes associated with a frequency that can vary infinitesimally around a specific value. They thus started to fix the radiation frequency in an interval [ν, ν + dν] where dν is infinitesimal.
They then multiplied the result by the mean vibration energy E(T) of each mode. Assuming that these modes are distributed following a Maxwell-Botlzmann distribution, integrating and averaging gives
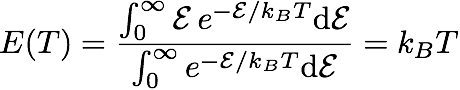
I will try to roughly explain what lies behind this formula. The numerator gives the total energy once summed over all modes (the energy varies from 0 to infinity). The denominators allows to get the mean value by dividing by the number of modes.
[image credits: mine]
The important point here is that they assume the energy can vary continuously between 0 and infinity.
As shown on the figure on the right, this works this time very well at low frequency (large wavelengths), but fails for larger frequencies (smaller wavelengths).
Moreover, one cannot use this formula to derive the total energy of a back body. The calculation diverges towards infinity, which makes no sense.
This can be seen by evaluating the area below the orange curve, which is finite. This contrasts with the blue curve where the energy is finite.

[image credits: Wikipedia ]
AND HERE COMES PLANCK
Both previous explanations were fine only if we would restrict ourselves to a part of the black-body spectrum.
In 1900, Max Planck himself found the solution. He derived an empirical formula that was agreeing with uRJ for the large wavelengths and with uW for the small wavelengths,
u(ν,T) = (ν/c)3 (8 π h) / [ exp( - h ν/ (kB T)) - 1 ]
This formula only depends on a single parameter, h, that is the famous Planck constant, a universal constant of physics,
h = 6.6260700 × 10−34 J s
This formula represents the first apparition of the Planck constant in physics, but actually not the last apparition at all, as I will show it in my next quantum mechanics articles.
Max Planck formula has the advantages of reproducing perfectly well black-body data.
In order to justify his formula, Plank follows the reasoning of Rayleigh and Jeans. In the following, I make the story much easier in order to get directly to the point.
We start from the mean energy calculated with the integral above. Instead of integrating over all energy modes ranging from 0 to infinity, we replace the integral by sums over a infinite number of discrete energy modes. By enforcing the nth energy mode to be equal to n ε, we get
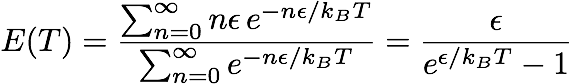
If we take the limit of the right-hand side for ε going towards 0, we find back the result of Rayleigh-Jeans uRJ. However, Planck introduced the idea that the energy was quantized and did not take that limit. He imposes instead that
ε = h ν,
which leads to his formula.
A NOVEL IDEA AND PLANCK MISINTERPRETATION
In order to explain the radiation pattern of a black-body, Planck has introduced the idea that the energy E was quantized. It can only take specific values under the form of
En = n h ν
with n being a positive integer.
The energy quantum is thus proportional to the frequency, and the proportionality constant is not a simple parameter anymore. It plays a big role in defining the energy quantum. The Planck constant h is actually the physics constant of quantum mechanics.
Planck however believed that the atoms of the cavity were radiating discrete amounts of energy quanta. This was wrong, and Einstein corrected it a few years later. But this is the topic of my next post :)
SUMMARY
In this post, I have discussed the issues related to macroscopic systems called black bodies. I have introduced the issues with their radiation pattern that classical physics was not capable to explain, and detailed different attempts to explain it.
I introduced the ideas of Wien and Rayleigh and-Jeans for explaining for the black=-body energy density, and I ended up this article with the amazing idea of Planck, stating that the black-body behavior could be explained by considering that the energy is quantized.
In the next post, I will discuss how Einstein concluded that energy quantization was actually not a property of the black body, but a general property of all radiation.
