Here is a problem done by standard orthodox methods.
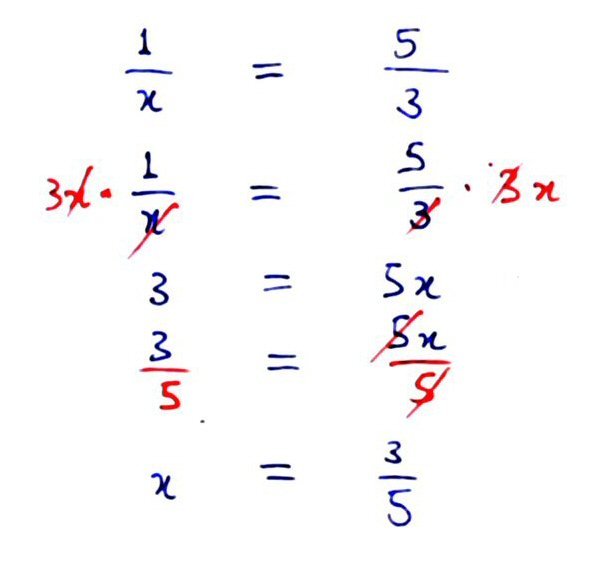
We multiply both sides of tbe equation by 3x, which is a legit procedure. On the LHS, we cancel the x's, and on the RHS, we cancel the 3s. We now have 3 = 5x. We need to get rid of the 5, so we divide both sides by 5. After cancelling, we get 3/5 = x. Then by the Law of Symmetry (if A=B, then B=A), we can conclude that x = 3/5.
This takes 4 steps to solve. Is there a faster way? You can try the Escalator Trick
like this:-
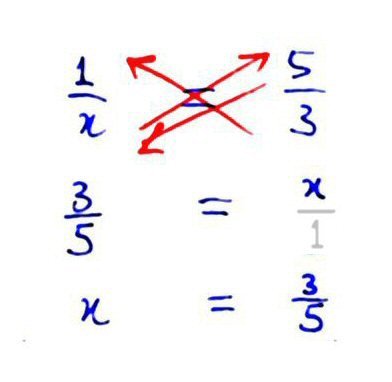
Move the x up the escalator to appear on top of the other side. Now 5 and 3 have to move. So 5 moves down the escalator to the bottom left side, and 3 moves up the escalator to the top of the left side. Again by the Law of Symmetry (if A=B, then B=A), we can conclude that x = 3/5.
Not bad. But it takes 2 steps. It there an even faster way?
Yes! Think of two chicken wings on a barbecue skewer. If you flip the skewer, both the chicken wings flip together.
Now we do this flipping for our equation.
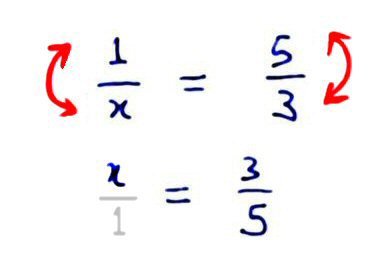
We invert (calculate the reciprocal) both the LHS and the RHS at the same time. And we get the answer immediately. The reason this works is because 1 ÷ (1/x) = x and 1 ÷ (5/3) = 3/5, and we are doing the same thing to both sides, so we still get things that are equal. Note that x/1 is the same as x. So we do not need to write the '/1' actually.
There we have it! This short-cut is flipping good, eh?
