In yesterday’s article I basically reviewed Counting, Addition and Multiplication via Set Theory in a more rigorous (but still accessible) setting. Hopefully we have some common understanding now.
Today I want to discuss this (see below).
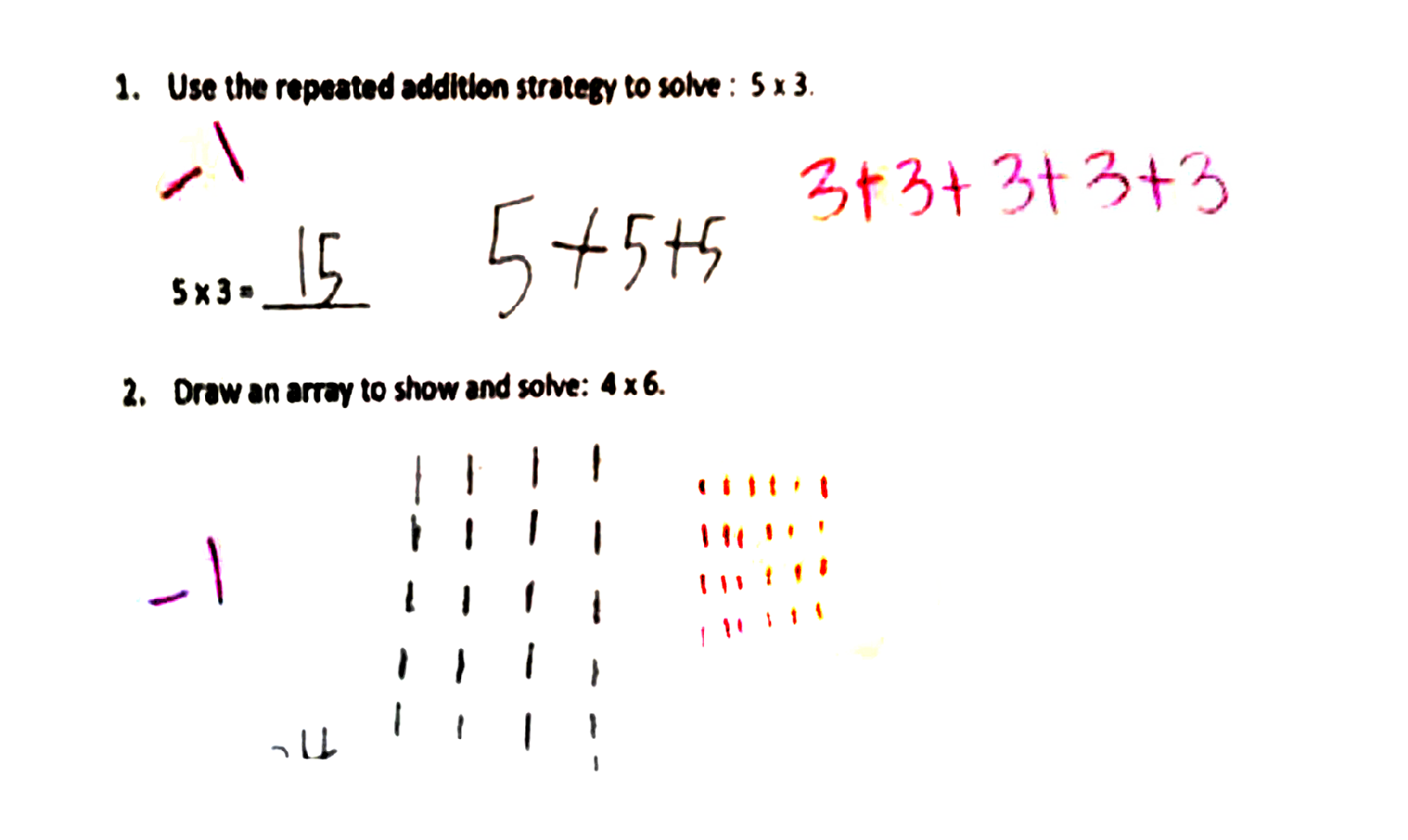
The student got marked wrong because she did not answer the question in the way that the teacher expected. For question 1, 5 × 3 was supposed to be 3 + 3 + 3 + 3 + 3. For question 2, the pupil was expected to draw 4 rows of 6 instead of 6 rows of 4.
Were the teacher’s own answers correct? For question 1, technically yes, because “5 × 3” literally means “5 times of 3” which means 3 appears 5 times in the addition i.e. 3 + 3 + 3 + 3 + 3. For question 2, “4 × 6” can indeed be represented by 4 rows of 6, but is it a must?
Should the teacher insist that that is the only way to answer the questions (as worded in the test)? Question 1, was worded with the instruction “use the repeated addition strategy”. Well, the pupil did use a repeated addition strategy. So technically, she is not wrong too. In fact her 5 + 5 + 5 is more efficient and she showed that at least she knew the Commutative Law, which was a higher level of understanding. For question 2, insisting on counting in rows could be a cultural bias as I mentioned in yesterday’s article. That means counting in rows instead of columns is something that is a practice/convention/habit only due to the culture or society one happens to be in, and this is not really something inherently mathematical, but more of a preference. Sometimes we don't realise that we are so used to thinking in a certain way, but we should be more open-minded and aware of other ways of thinking, or how other people from other ethnic cultures think. Besides ethnic culture, there is also a mathematics culture. Mathematicians look beyond superfical constructs of ethnic culture and see the connection between things, and have a sense of what is important and not important, as far as mathematical patterns are concerned. Insisting in a fixed way of seeing things is not of the mathematical culture, while being able to see the connection between a rectangular array and its transposed version is.
Was the teacher too “pedantic”? I say, if you want to be pedantic, you might as well go all the way. When setting test or quiz questions, teachers should be mindful of how the pupil will interpret it from his/her point of view. If you want the question to be answered in a specific way, then make sure that your rubric is phrased appropriately for that. The wording “use the repeated addition strategy” does not distinguish between 5 + 5 + 5 and 3 + 3 + 3 + 3 + 3. If the latter was meant, then the question could mention something about the literal meaning of 5 × 3. If we as educators want to be pedantic (or having "high intellectual standards"), we should be pedantic on ourselves first, to model ourselves as personal examples.
By the way, the word “solve” in mathematics usually means to “solve an equation”. Or to “solve a problem”. If you want the pupil to calculate something, then use words like “calculate” and “evaluate”. There is a list of these words used with Bloom’s Taxonomy and the word used should specify what you really want the pupil to do. Arithmetic is not much of a problem to "solve". Maybe the real problem to solve is the teachers Content Knowledge (deep and not superficial understanding of “simple” mathematics, like Set Theory, Number Theory etc.), Pedagogical Knowledge (e.g. Bloom’s Taxonomy) and Pedagogical Content Knowledge (how to combine knowledge of pedagogy, psychology etc to bring the deep understanding of the content, in a way that is understood by the pupils).
This brings us to questions such as: What is it that you are teaching? Are you preparing the pupil for future learning? Are you preparing the pupil for life? What values are you trying to inculcate? What values are you actually exemplifying as a teacher? What attitudes do the pupils actually end up learning? We should all appreciate the difference between the intended curriculum (what those air-heads at the government departments plan), the implemented curriculum (what teachers interpret or misinterpret "the curriculum" to be, and what they really do in class) and the achieved curriculum (what pupils end up learning, including attitudes like “maths is just following procedures”, “you need to be closed-minded to do well in math”). This makes you think, doesn’t it?
