Hey folks!
How's life? Hope everyone of you are having a great time! As far as I'm concerned, everything is fine right now. Only bad thing is vacations are over now so I'm forced to return to the hectic city I live in. At least it means I will now have access to my desktop which I can't live without. I'm a workaholic. So the good news is I'm back with another Cartography blog as promised in my previous introductory posts. As always I'm in a hurry so no time to play around! Let's do this!
As stated and promised in my previous Cartography post, this is the sixth part regarding the science and art of creating 2D depictions of 3D objects with precision. This is a great opportunity for me to share advanced technical information concerning the main categories of Azimuthal Projections that are utilized by Cartographers and Engineers in general nowadays. We will also take a deeper look at the four of all five main categories of Azimuthal Projections that are broadly used, as the Stereographic Azimuthal Projection was included in a previous blog, so stay focused!
Once again, I need to clarify that these are still introductory posts as stated. This basically means that I will be presenting complex information in a simplified manner so that nobody gets hurt or bored. Kidding. Not. I promise that I will constantly try to reward your attention with failed jokes. Apart from having fun, there's a high chance of learning a thing or two by reading through this blog, so stay tuned!

Image Source: pixabay.com
Azimuthal Projections
Azimuthal Projections are broadly used by Catographers and Engineers in general nowadays. Development in various correlated scientific fields has implemented growth in demand for precise cartographic projections that can be utilized in several different professions. Therefore, this specific sort of projections is mainly used by professionals for technical purposes as it provides great accuracy regarding angles and directions due to the unique, useful attributes possessed and demonstrated.
All Azimuthal Projections are depicted on a flat surface which can be centered anywhere on the reference sphere's surface. All sorts of distortion observed and included in Azimuthal Projections are absolutely symmetrical to the center of the reference sphere. This specific point is actually intersected by the z axis, which is vertical to the plane of the projection. Furthermore, all maximum circles (Parallels) presented in the middle of the projection are depicted as straight lines, which accurately represent azimuthal angles towards the direction of the projection's center and vice versa in relation to any specific point on the projection's surface.
All Azimuthal Projections that utilize the same primary scale factor value concure perfectly in the center of the projection. Slight differences between various Azimuthal Projections are mainly spotted along the direction of the maximum circles (Parallels), which are depicted as straight lines , starting from the center of the projection and moving towards the edges. Those slight differences are mainly induced by the variation of the scale factor value which is proportional to the distance from a particular point of the projection's surface to the center of the projection.
As a result, due to the fact that spatial distortion is distributed symmetrically around a specific center, this category of projections is extremely useful for the observation, depiction and study of areas with similar geometric dimensions in all directions. Even though it is practically and geometrically possible to design and produce an infinite number of different Azimuthal Projections, there are only five main categories that are broadly used nowadays. I've shared advanced technical information regarding the Azimuthal Steregoraphic Projection in a previous blog as mentioned in the introduction, so we will only be discussing the four main categories of Azimuthal Projections that are demonstrated below:
Lambert Azimuthal Equal-Area Projection
Azimuthal Equidistant Projection
Orthographic Azimuthal Projection
Gnomonic Azimuthal Projection
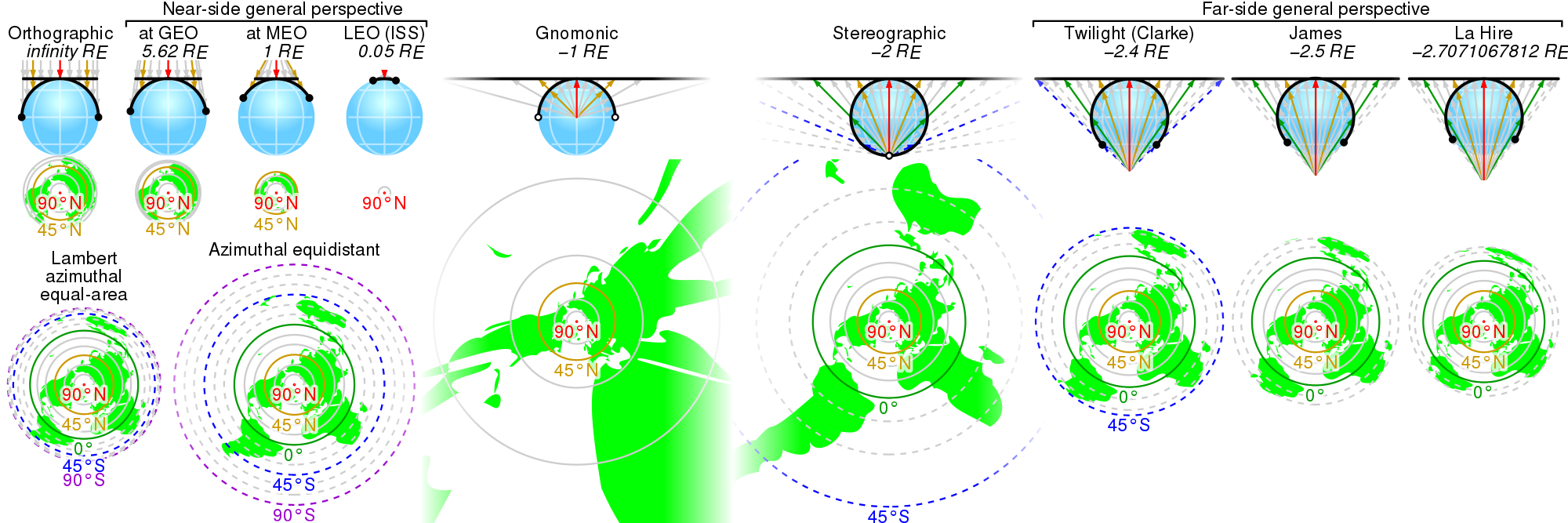
Azimuthal Projections Comparison./ Image Source: commons.wikimedia.org
Lambert Azimuthal Equal-Area Projection
The Lambert Azimuthal Projection is broadly used in various professional and scientific fields nowadays. This is also an equal-area projection, which possesses significant geometric attributes regarding the precise depiction of angles and directions, mainly due to the fact that it belongs to the category of Azimuthal Projections. Obviously, spatial distortion is symmetrically distributed around the center, which usually is a specific point on the projection plane that could be situated anywhere on the projection's surface. Therefore, this specific projection is rather useful in cases of areas of equal longtitude and latitude variation.
The Lambert Azimuthal Projection is frequently utilized in the design and construction of Atlases, as well as for various sorts of mappings serving as tools of statistical analysis and its usage is therefore highly recommended by the European Environment Agency. The global projection of the world designed through the utilization of the Lambert Azimuthal Projection has its center at the point where the Meridian of Greenwich which is also known as the Prime Meridian intersects the Equator, while its antipode is situated at 180 degrees East. The following map is NOT a flat-Earth map. Get real, flat-Earthers.
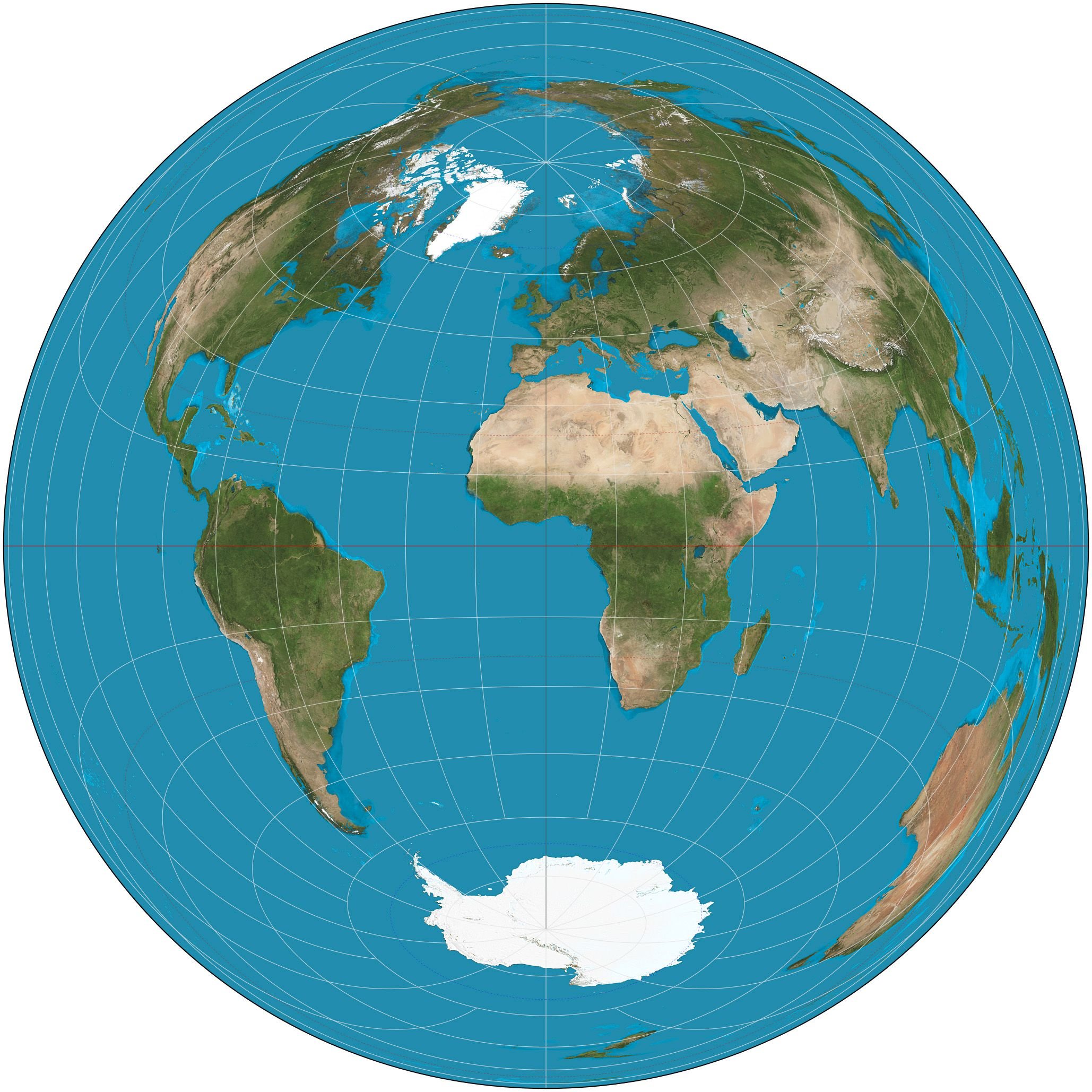
Lambert Azimuthal Equal-Area Projection./ Image Source: en.wikipedia.org
Azimuthal Equidistant Projection
The Azimuthal Equidistant Projection is another significant projection utilized by scientists and professionals in general nowadays. Linear scale is uniformly distributed along the straight lines intersecting the center of the projection, which is a rather important and unique attribute making this projection extremely useful. Inevitably, as a result of this attribute's effect, all points' locations are defined by two quantities: distance from the center of the projection and relative location. It is worth noting at this point that directions and distances between specific points, that are connected by Parallels which do not intersect the center of the projection, are not depicted with precision.
This projection is rather useful in cases where the observation of the motion of vehicles, or various sorts of artificial entities or natural quantities in general, is the primary objective, especially in cases where those motions refer to a central point in space. For instance, the transmission of seismic or radio waves can be accurately represented by utilizing this projection. The Azimuthal Equidistant Projection can be utilized to represent the whole reference sphere's surface, which is a great advantage and another significant attribute, as most Azimuthal Projections can only represent one hemisphere or less. I promise these are not flat-Earth maps.
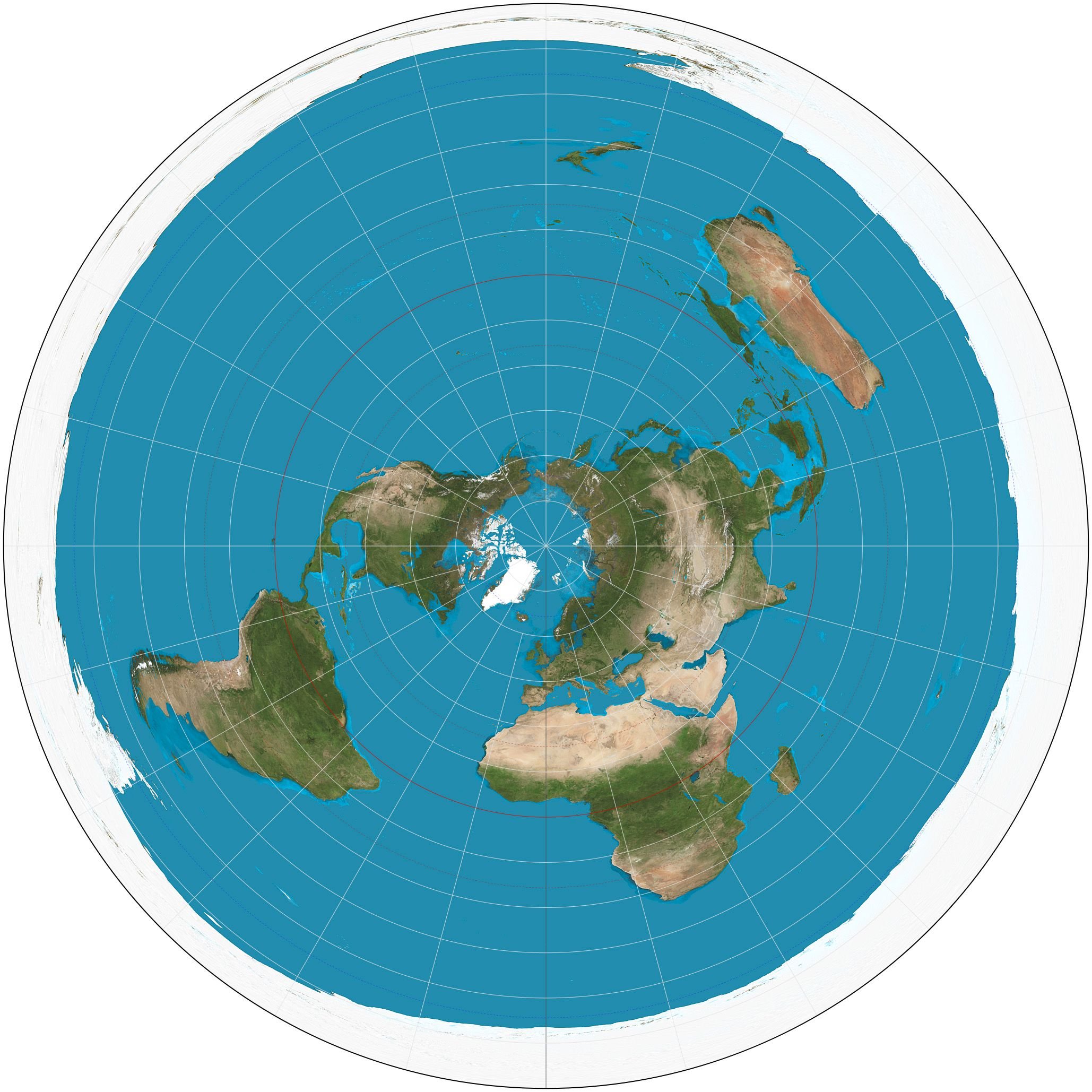
Azimuthal Equidistant Projection./ Image Source: en.wikipedia.org
Orthographic Azimuthal Projection
The Orthographic Azimuthal Projection is another significnt projection that was first mentioned and utilized by Hipparchus in ancient Greece. Although this specific projection is not utilized in the design and construction of global maps, due to the magnitude of distortion regarding shape and size in areas close to the boundaries of the projection, it does include great precision along Parallels that intersect the center of the projection. It is worth noting at this point that distortion regarding surfaces and angles is not obvious to the average user. The design of orthographic maps is relatively easy with nowadays' technological advancement regarding instruments and computers.
This particular projection presents the reference sphere as observed from a huge distance, and therefore the spatial distortion included is acceptable for the map's purpose. As a result, this specific projection is rather useful in the design and construction of exhibition mappings, due to the fact that the Earth's sphericity is a top priority issue in such cases. Moreover, the Orthographic Projections is frequently utilized in the development of various mappings used in Atlases, as well as in the study of celestial bodies, which induced a high demand for orthographic mappings especially in recent years that we started exploring our solar system. I hope all flat-Earthers are gone by now.
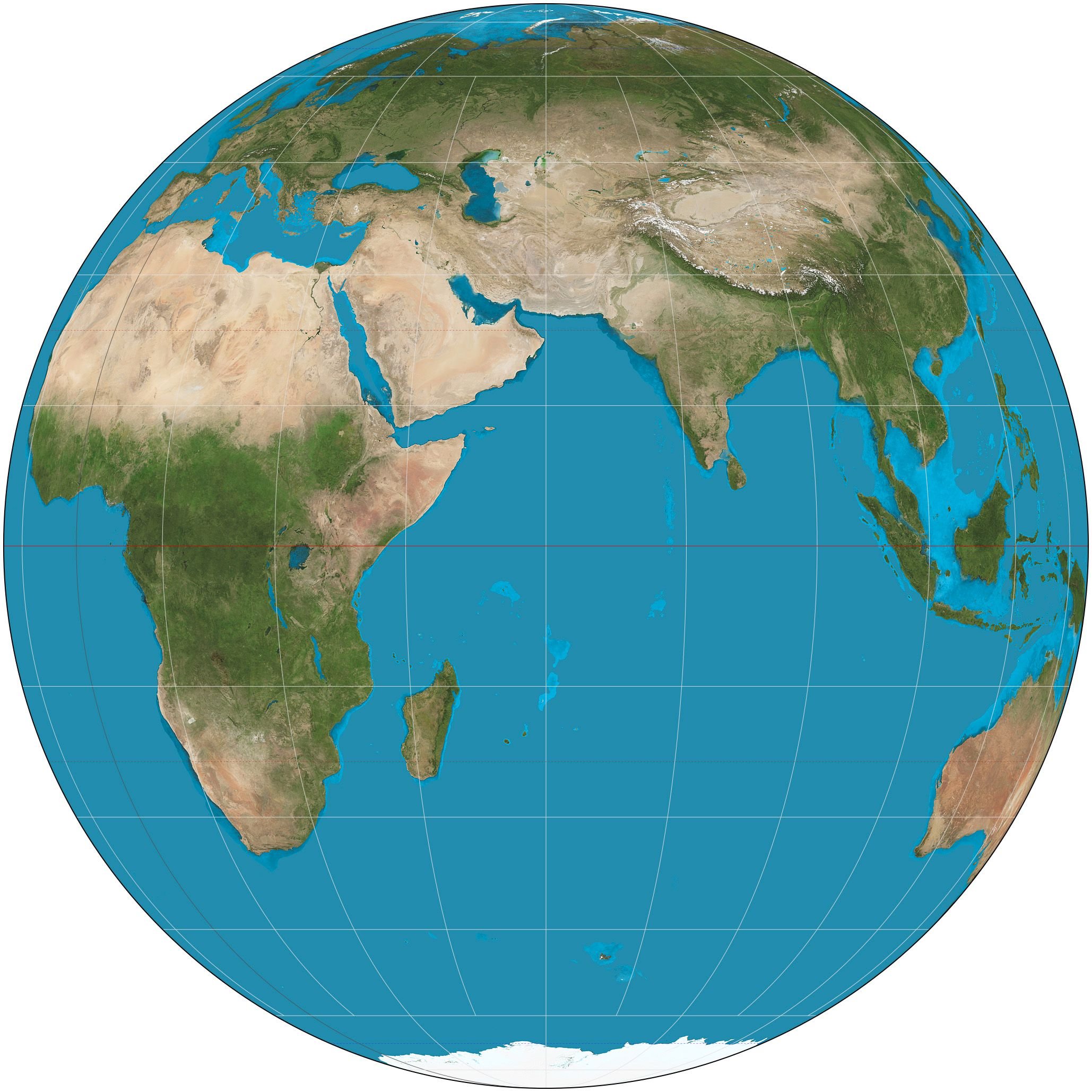
Orthographic Azimuthal Projection./ Image Source: en.wikipedia.org
Gnomonic Azimuthal Projection
The Gnomonic Azimuthal Projection is another significant projection included in the category of Azimuthal Projections. It is worth noting that all arcs of all Parallels are represented as straight lines in all areas of this projection's plane. This unique attribute possessed and demonstrated by the Gnomonic Projection makes this projection the perfect choice for the design and creation of mappings used for navigation purposes. Sailors using gnomonic maps can spot the trajectories that refer to the maximum circle (Parallel) by connecting the points of arrival and departure with straight lines on the gnomonic projection. In this way the shortest route between two points is spotted, however this is not the direction to follow in all cases.
This projection is designed and built in a similar manner to the Azimuthal Stereographic, which we talked about in a previous Cartography post. It can only depict a little less than one hemisphere of the reference sphere's surface, while distortion is distributed symmetrically around the tangent point. Regarding navigation, due to the fact that compass needles change direction as observers move along a maximum circle (Parallel), Engineers project trajectories depicted on the gnomonic grid to the Mercator plane in order to determine the curved trajectory with a series of successive straight lines of constant azimuthal angle. Nobody's perfect! Some people believe in the flat-Earth theory.
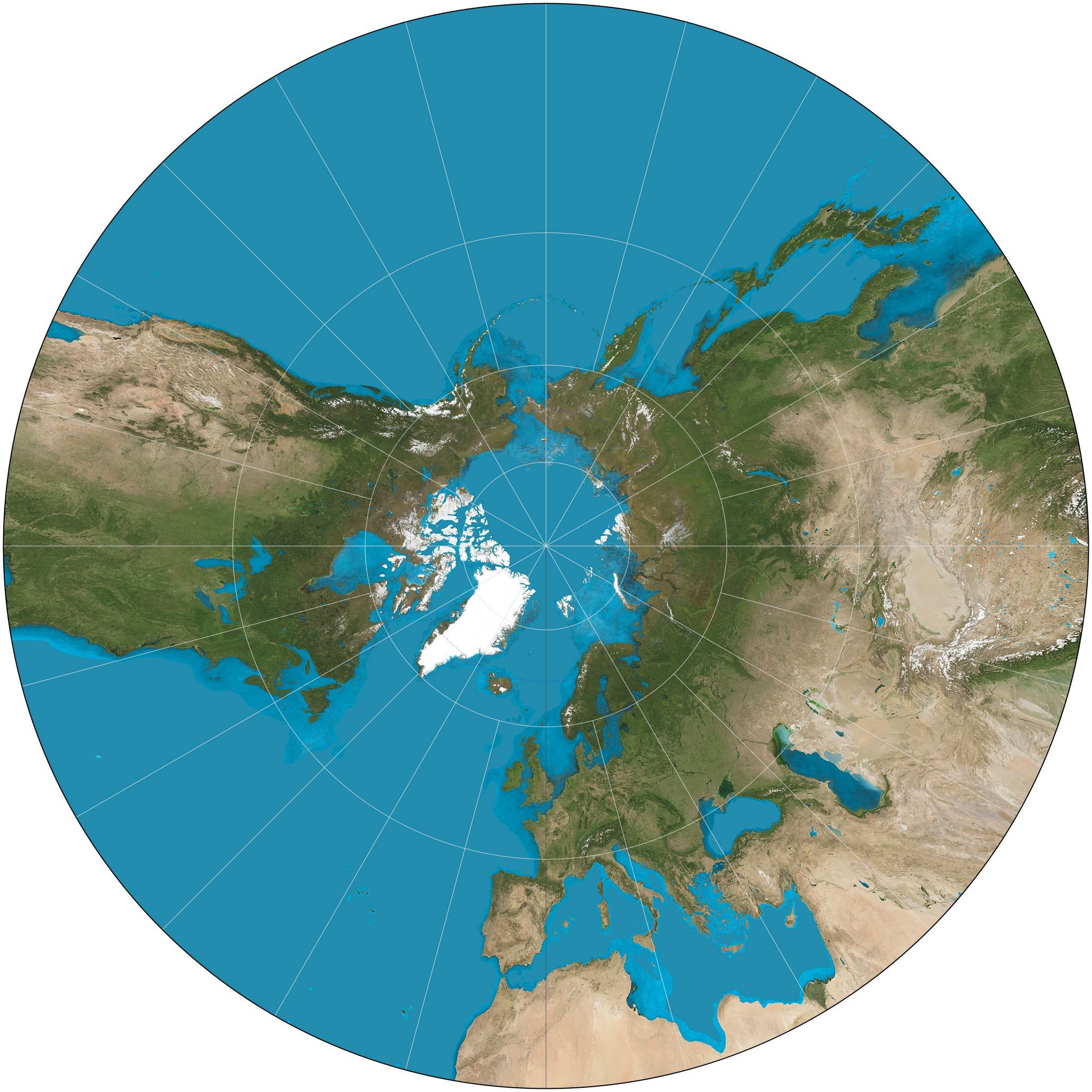
Gnomonic Azimuthal Projection./ Image Source: en.wikipedia.org
Alright, that's it for today guys! Hope you made it till this point and enjoyed this blog! That brings us to the end of this Cartography blog regarding Azimuthal Projections. I've mentioned before how projections are a vital part of the art and science of creating 2D depictions of our 3D world with precision and therefore we will be discussing all main categories one by one. Feel free to let me know if you do have any questions in the comments below and I promise I will do my best to provide detailed answers immediately. Follow me and stay tuned for more nerdy blogs!

IMAGE SOURCES:
REFERENCES:
University Textbooks & Course Lectures:
Χαρτογραφία Ι /Cartography I -TSOULOS LYSSANDROS(National Technical University of Athens, School of Rural & Surveying Engineering,Course Lectures)
Xαρτογραφία ΙΙ /Cartography II -NAKOS BYRON(National Technical University of Athens, School of Rural & Surveying Engineering,Course Lectures)
Στοιχεία Χαρτογραφίας,Πανεπιστημιακές Εκδόσεις Ε.Μ.Π. /Εlements of Cartography, University Publications NTUA - A.H. ROBINSON, J.L. MORRISON, S.C. GUPTILL, A.J. KIMERLING, P.C. MUEHRCKE,(National Technical University of Athens,School of Rural and Surveying Engineering, University Textbook)
Internet Links:
http://www.progonos.com/furuti/MapProj/Normal/ProjAz/projAz.html
http://northstar-www.dartmouth.edu/doc/idl/html_6.2/Azimuthal_Projections.html
https://www.wired.com/2014/11/get-to-know-a-projection-azimuthal-orthographic/


Thank you for your attention!
Hope you enjoyed this post and did learn a thing or two.
Follow me and stay tuned for more engineering blogs.
Highest Regards
@lordneroo
