Hey folks!
What's been up? I sincerely hope each and everyone of you are having a wonderful time. Life is great right now so I try to enjoy the simple things. Sharing precious moments with friends, loved ones and pets! Business always comes first though, so it's been another couple of exhausting days, however I'm back in business with another Cartography blog.
As promised in my previous Cartography blog, this is the fourth part regarding the art of creating accurate depictions of our 3D world on 2D surfaces. This time I'm taking the chance to share broad technical information concerning conformal projections, which is one of the three main categories of cartographic projections utilized nowadays. We will also take a deeper look at the four different types of conformal projections that are mainly used, so bare with me!
I've decided I will make more of those blogs as I need space between different chapters in order to provide detailed and readable blogs. I respect Cartography and besides there are no limitations. These are my Steem Cartography Lectures after all. Sure, dude. Let's always keep in mind that these are still introductory posts. What does that mean? It basically means that I will try to present general information by approaching business in a humoristic manner. There's always a high chance of learning a thing or two by reading through these blogs, so stay tuned!

Image Source: pixabay.com
As mentioned in a previous Cartography blog, all transformations used when designing cartographic projections induce spatial distortion regarding the depiction of the natural terrestrial surface, therefore all projections of 3D objects on 2D surfaces include errors concerning spatial distribution. There's a range of different sorts of distortion regarding the nature of this phenomenon and the patterns followed in a projection. In order to better comprehend the concept of spatial distortion we will take a deep look at the various sorts of conformal projections and the different geographical attributes utilized by different projections.
Conformal Projections
Maps that are being used in fields which demand accuracy regarding the analysis and development of a precise register of motions and angular correlations between geographic entities utilize conformal projections. The definition of distortion differs in cases of conformal projections due to the fact that it is all a matter of the scale factor value. Being the only variable quantity between different points on a conformal projection's surface, it induces distortion regarding the depiction of size in different areas and therefore the accuracy regarding geographic locations is the same in all areas of the projection.
Due to this variation of the scale factor, Cartographers have decided to refer to the projection's primary scale as the map scale, whereas areas depicted with a different scale factor are mainly considered as reduction or magnification surfaces respectively. There are four types of conformal projections that are broadly used by Cartographers and Engineers of all sorts in general nowadays, as demonstrated below:
Mercator Projection
Transverse Mercator Projection
Lambert Conical Projection
Stereographic Azimuthal Projection
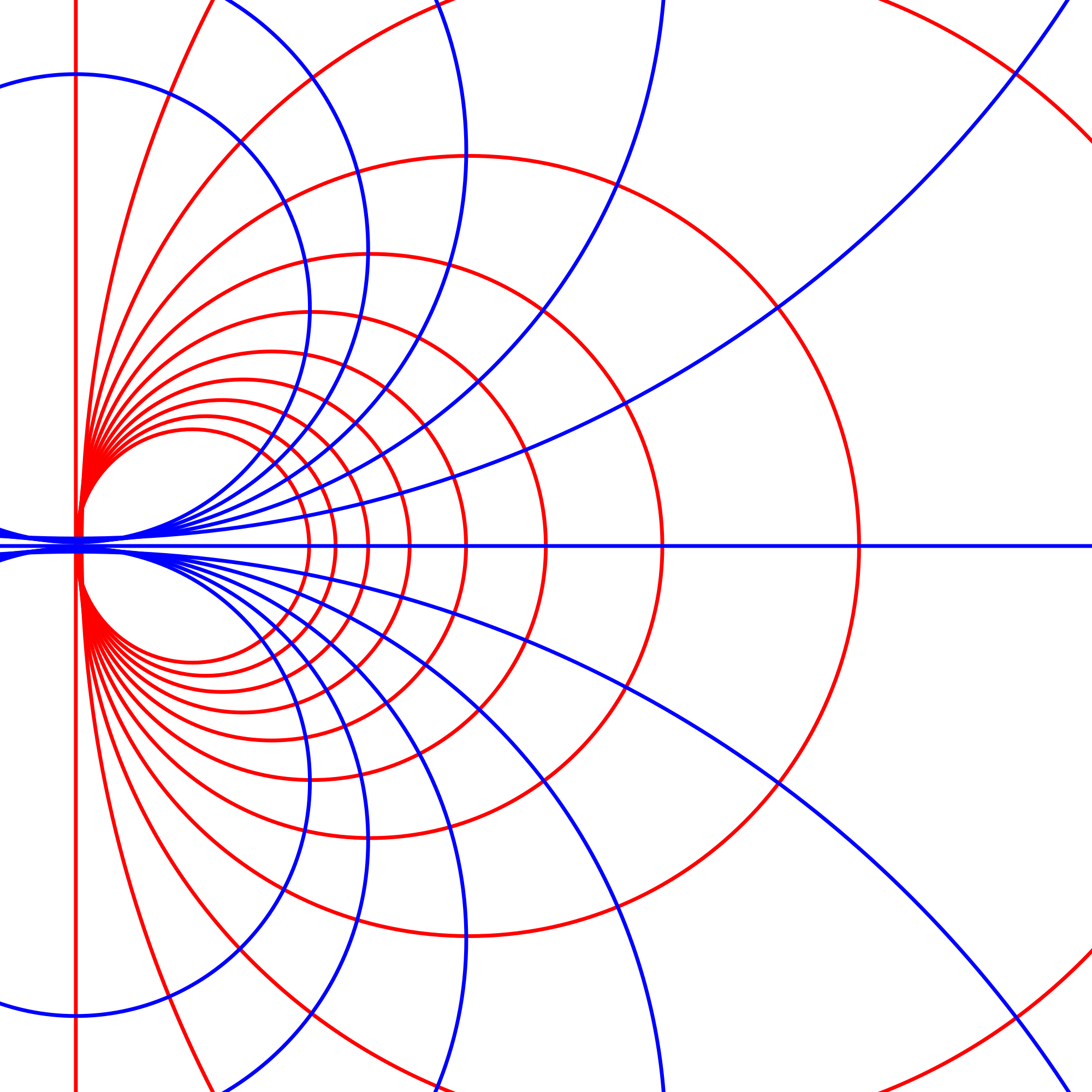
Conformal Geometry - Mobius Transformation./ Image Source:en.wikipedia.org
The Mercator Projection is the most popular amongst all conformal projections due to its frequent utilization mostly by sailors, however the Stereographic Azimuthal Projection is broadly used nowadays as well. The most commonly used conformal projections regarding Cartographers though are definitely the Transverse Mercator Projection and the Lambert Conical Projection. Let's take a deeper look at each one of those four types of conformal projections.
Mercator Projection
The Mercator Projection is probably the most popular projection that was ever designed. Created by Gerardus Mercator (5 March 1512 – 2 December 1594), the Mercator Projection was mainly designed and mostly used for navigation purposes as it offers the significant attribute of depicting trajectories of constant azimuth angle as straight lines. Meridians and Parallels are also depicted as straight lines and therefore it is obvious that the Mercator Projection does not demonstrate actual directions.
The primary reference line is the Equator, which basically means that the scale factor on the Equator equals 1,0. The rate at which the scale factor value increases depends on the latitude of any specific point. As a result, areas closer to the poles are depicted with a larger scale factor and therefore this sort of projection is only useful for navigation purposes. Since the Earth is actually round (Yes, flat-Earthers, it's round ) we can change the primary reference line by rotating the projection on the Sphere's surface by 90 degrees. That way the new primary reference line is a Meridian and this new projection is known as Transverse Mercator Projection.
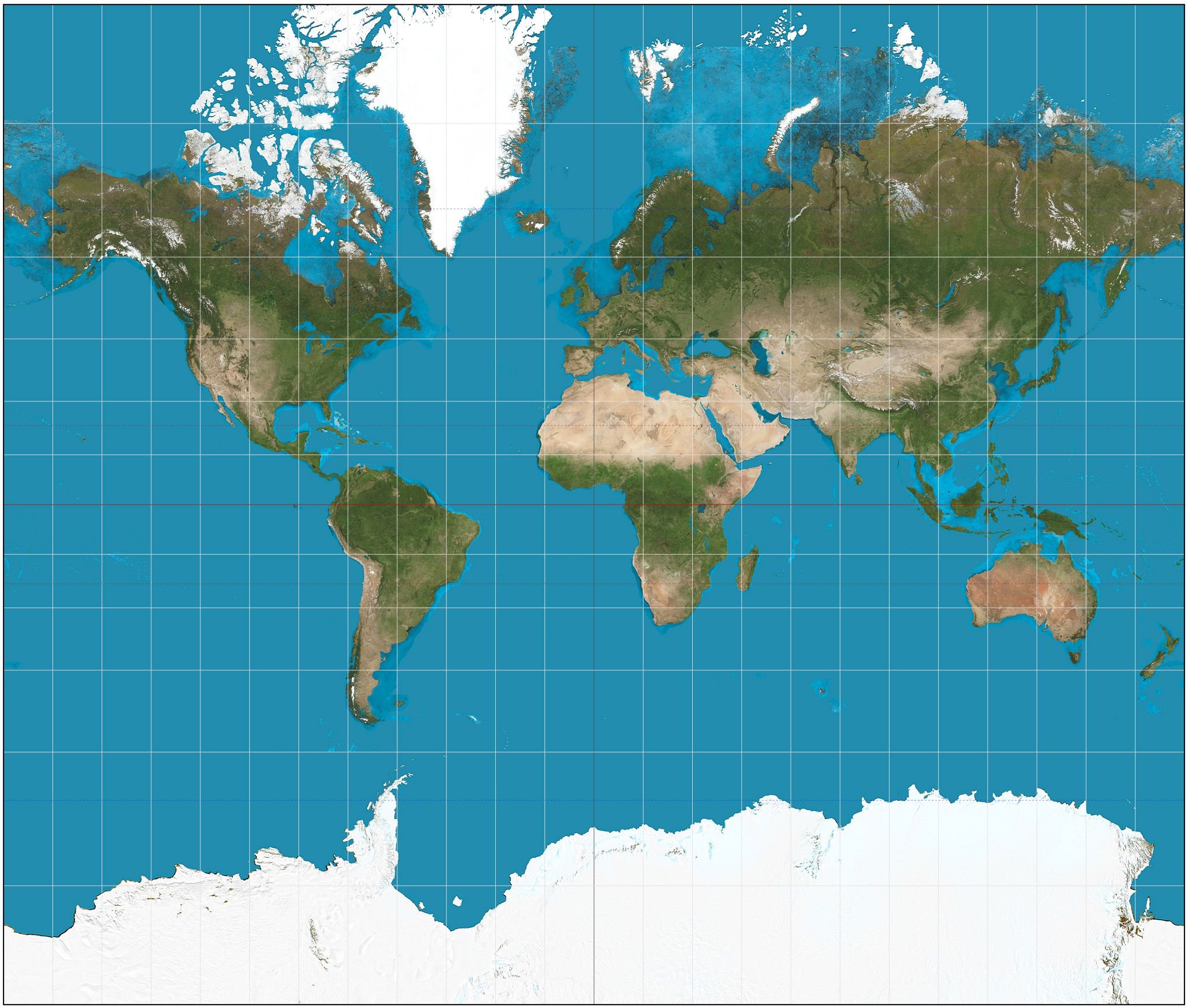
Mercator Projection./ Image Source:en.wikipedia.org
Transverse Mercator Projection
The Transverse Mercator Projection is a conformal projection that lacks the Mercator Projection's attribute of depicting trajectories of constant azimuth angle as straight lines. As a result, since the scale factor increase as we move away from the primary Meridian, this specific projection is only useful when studying small areas along the primary Meridian. The parallels of the grid, which represent the lines of equal scale variation, are small circles which are parallel to the primary Meridian's direction.
Inevitably, the Earth's surface is frequently represented by a series of narrow geographic stripes which expand from North to South and a sequence of long geographic stripes which expand from East to West. Each lane represents a unique intersecting Transverse Mercator Projection. In recent years, this projection has been used frequently and broadly in the design and construction of topographic mappings, especially by Cartographers in the US and the UK. Moreover the Universe Transverse Mercator (UTM), which is a global system of flat coordinates, was designed based on the Transverse Mercator Projection. Not what you thought, flat-Earthers.
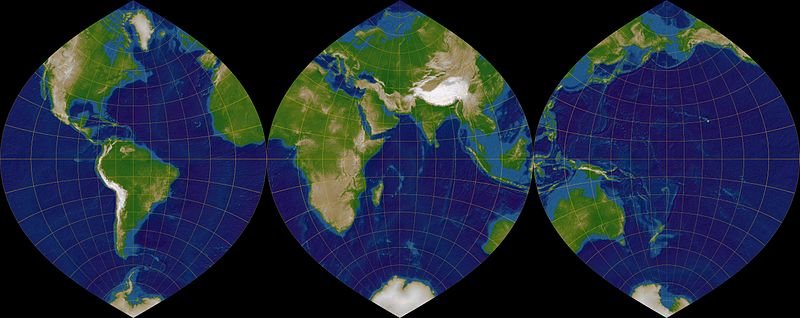
Transverse Mercator Projection - Meridian Stripes./ Image Source:commons.wikimedia.org
Lambert Conical Projection
The Lambert Conical Projection is another category of conformal projections which comes with the main characteristic of depicting Parallels as concentrical and equidistant, while depicting Meridians as straight lines that intersect the Parallels at 90 degrees. The scale factor equals less than 1,0 in areas situated between the primary Parallels and increases significantly above the value of 1,0 in areas situated outside of those boundaries set by the primary Parallels.
Distortion in areas located between the primary Parallels, as well as areas of the projection situated close to the boundaries set by those is relatively small. Therefore the Lambert Conical Projection provides extremeley accurate correlations of geographic entities' shapes and orientation for zones of the sphere which expand from East to West and have a relatively small value of latitude. Thus, this specific projection is utilized especially for aeronavigation purposes. Furthermore, it is often used in the construction of topographic and meteorological maps.
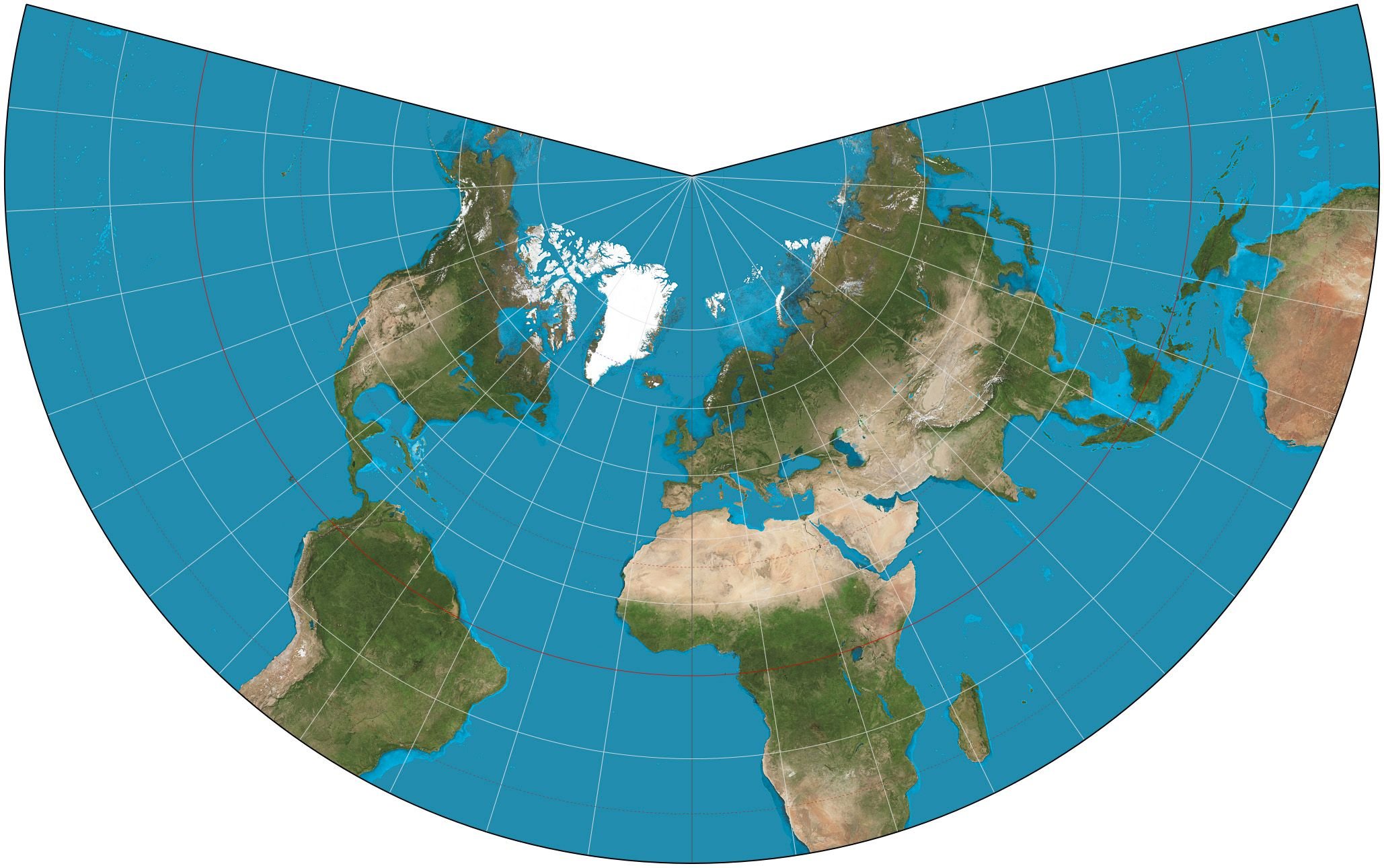
Lambert Conical Projection./ Image Source:en.wikipedia.org
Stereographic Azimuthal Projection
The Stereographic Azimuthal Projection is a very unique category of conformal projections due to the fundamental differences in the nature of spatial distortion demonstrated. In this particular projection the scale factor changes according to a point's distance from the central reference point of the projection. As a result, the farther away we move from the central reference point of the projection, the more spatial distortion values increase. This serves as a significant advantage for Cartographers, especially in cases where the shapes of the surfaces depicted are relatively compact.
Due to its unique characteristics and attributes, and taking into consideration the accurate preservation of shapes provided, it is safe to say that this certain category of conformal projections is the most efficient and precise amongst those commonly used for navigation purposes in particular. This projection is also frequently utilized in the creation of precise, quality mappings of large continents in spite of the fact that the projection's scale changes significantly as distances from the primary reference point increase. It is worth noting that all Meridians are depicted as straight lines, whereas Parallels are depicted as concentric circles.
Stereographic Azimuthal Projection./ Image Source:en.wikipedia.org
Alright, that's it for today guys! This brings us to the end of this Cartography blog regarding Conformal Projections. As promised in the introduction, I will upload two more blogs regarding cartographic transformations as there are two more main categories to analyze and discuss. I've mentioned before that projections are a vital part of the scientific field of creating accurate 2D depictions of our 3D world and therefore we will be discussing all three main categories one by one. If you do have any questions feel free to let me know in the comments below and I will do my best to provide prompt and detailed answers. Hope you enjoyed this blog! Follow me and stay tuned for more Engineering blogs! :)

IMAGE SOURCES:
REFERENCES:
University Textbooks & Course Lectures:
Στοιχεία Χαρτογραφίας,Πανεπιστημιακές Εκδόσεις Ε.Μ.Π. / Εlements of Cartography, University Publications NTUA - ROBINSON, MORRISON, GUPTILL, KIMERLING, MUEHRCKE(National Technical University of Athens, School of Rural and Surveying Engineering, University Textbook)
Χαρτογραφία Ι / Cartography I - TSOULOS LYSSANDROS(National Technical University of Athens, School of Rural & Surveying Engineering, Course Lectures)
Xαρτογραφία ΙΙ / Cartography II - NAKOS BYRON(National Technical University of Athens, School of Rural & Surveying Engineering, Course Lectures)
Internet Links:
http://www.progonos.com/furuti/MapProj/Dither/ProjConf/projConf.html
http://axismaps.github.io/thematic-cartography/articles/projections.html
https://gisgeography.com/utm-universal-transverse-mercator-projection/
https://gisgeography.com/conic-projection-lambert-albers-polyconic/
https://gisgeography.com/azimuthal-projection-orthographic-stereographic-gnomonic/


Thank you for your attention!
Hope you enjoyed this post and did learn a thing or two.
Follow me and stay tuned for more engineering blogs.
Highest Regards
@lordneroo
