Hilbert's Grand Hotel Paradox

I've had a thing for brain teasers since I was a young boy at school. Recently, I re-initiated this interest through reading (and posting) about cool mathematical paradoxes.
You can check out my recent posts about The Napkin Ring Paradox as well as The Zipf's Law

So, today's selection is about a counter-intuitive paradox called Hilbert's Grand Hotel Paradox.

Quick history..

Hilbert's Paradox is actually attributed to David Hilbert, a German Mathematician who introduced the concept in one of his lectures back in 1924, and then later popularized via Russian Physicist George Gamow.

The Fun!

The concept relates to infinite sets, and with infinity, you can always expect fascinating and at times counter-intuitive results.
So, let us consider the Grand Hotel of our dear Hilbert.

This imaginary hotel is deemed to have a countably infinite number of rooms. Pretty big huh ?

Cool Fact: When counting in infinity, and using the term countably infinite, we refer to the fact that we can actually count the rooms, i.e. we can say room #1, room #2,...yet due to being infinite, we can keep counting, well, till infinity. As opposed to uncountably infinite, whereby you cannot even count the numbers, you wouldn't even know where to start since it would include all REAL numbers.

So the hotel has a No Vacancy sign on top of it, whereby all of the rooms are currently occupied.

Illustration of current occupancy of Hilbert's Hotel

The somewhat simple case

A new guest comes to the hotel, and needs a place to stay. Now unfortunately, all the rooms of the hotel are already occupied, so there is no place for the new guest to visit.

Unless..Infinity plays its counter-intuitive tricks.

So the hotel's smart manager makes a cool decision, and asks every guest to move to the following room.
Whereby guest currently staying at room 1, moves to room 2,
and then guest at room 2, moves to room 3,
and so on and so forth... (avoiding counting to infinity to keep you guys reading)

New Guest shows up: shifting all guests one room ahead

So now we actually have a room for our new guest to stay at, being room #1. This is basically due to one of the cool facts about infinity, whereby adding a number to infinity, yields, infinity..
so ∞ + 1 = ∞

Now, let us consider the other way around, whereby one of the guests decided to leave the hotel. Will the hotel lose its fully booked status?

Well, you probably guessed it. Not at all.

Since the manager would just need to do the reverse of what he did before. When the guest moves away from room #1, he would politely ask guest 2 to move to room #1, and guest 3 to move to room #2,...

Guest left room #1, shift every one back one room back

And again, due to the property of infinity of ∞ - 1 = ∞, we still have an infinitely number of rooms, fully occupied.

Making things a bit more complex

This was fully manageable by the hotel manager for a while, whereby he was getting 1, 2, 50, 60 additional guests to the hotel, and by shifting all the guests to the +1, +2, +50, +60th room, this was all taken care of.
Cool Fact: ∞ + n = ∞, with n being any finite number.

Until one day, a touristic bus stopped by the hotel, and the bus had an infinite number of passengers, who all needed a room at the hotel.

Can those new passengers be fit into the hotel?

Well, the manager said yes! What he asked his poor guests this time, was to actually move while leaving a single empty room in between.
So, guest at room #1, would move to room #2,
guest at room #2, would move to room #4,
guest at room #3, would move to room #6...

Then, the passengers would each fill in the empty rooms.
So passenger 1 would go to room #1,
passenger 2 would go to room #3,....

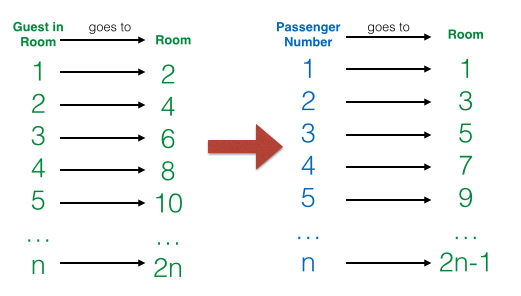
New rules for moving guests to accommodate infinite new number of guests

The idea behind this was splitting the infinite amount of rooms, into odd and even numbers, and filling both infinite sets of guests and passengers into the rooms. Sounds pretty crazy .. but it works!

Through this, everyone has a room, and the hotel was fully booked.

Things get crazy!

Due to the increasing popularity of this marvelous hotel, on a summer evening, the manager got his biggest visitors yet, an infinite number of buses, each with an infinite number of passengers, arrived to stay at his hotel.

Now the manager, a seemingly bright math guy, recalled that there are infinitely many prime numbers (2, 3, 5, 7, 11, 13,...). So he decided to use that for shifting his guests.

The current occupants of the hotel, would move to rooms which are power of the first prime, being number 2.
Meaning guest in room #1, would move to room 2¹, being room 2
guest in room #2, would move to room 2², being room 4
guest in room #3, would move to room 2³, being room 8...

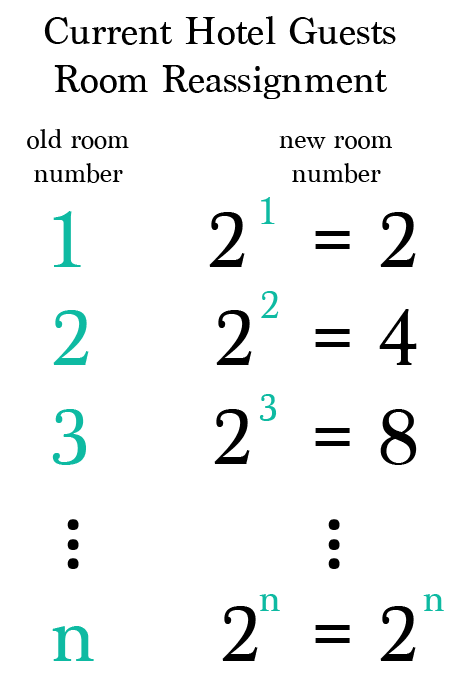
Moving current guests to powers of first prime

And then the passengers of the first bus, would go to rooms which are powers of the second prime, being number 3.
So bus 1's passenger 1 would go to room 3¹, being room 3,
and bus 1's passenger 2 would go to room 3², being room 9,...

And similarly, bus 2 would have his passengers go to powers of prime 5, etc...

Hotel and bus passengers movements

So finally, after all movements are done, we would end up with the following combination, with Hilbert's Grand Hotel fitting into all its guests

Final matching between guests, passengers, and rooms

Yet, the only drawback (or advantage) of this approach is that the "No vacancy" sign will need to be turned of, as a lot of rooms will be left empty, which are basically the ones that are non-prime numbers nor powers of prime numbers, such as rooms 6, 14, 15...

The above approach is what is called a pairing function (as in paring guests to rooms), and the one used was actually prime powers pairing. There are other approaches which could also be used to resolve the vacancy problem in the latter case, including prime factorization method, which also yields to vacancies in the hotel booking.
Yet, for optimized booking, the manager could have used one of the following alternatives: Interleaving method, the Triangular number method, or the Arbitrary enumeration method, which actually pair the guests with the rooms on a 1 to 1 basis, yet those would be topics for future posts, or you can just check their further approaches in reference 1 below.

And finally, there are other more complex variants of the last scenario, which add infinite levels of nesting (infinite variants of buses,...) and rendering the count of guests, uncountably infinite, and hence negate the original statement of countably finite rooms. At which case the hotel will definitely not be able to fit the guests

Hope you found this as mind-boggling and fun as I did!

Till next time!

@mcfarhat

References:

Photo Credits:

Founder of Arab Steem
Arab Steem is a community project to expand Steemit to the Arab world, by supporting the existing Arab steemians and promoting others to join.
You can connect with us on @arabsteem or via discord channel https://discord.gg/g98z2Ya
Your support is well appreciated!

Proud Member Of

steemSTEM: SteemSTEM is a project that aims to increase both the quality as well as visibility of Science, Technology, Engineering and Mathematics (and Health). You can check out some great scientific articles via visiting the project tag #steemSTEM , project page @steemstem, or connecting with us on chat https://steemit.chat/channel/steemSTEM
MAP(Minnows Accelerator Project): MAP is a growing community helping talented minnows accelerate their growth on Steemit.
To join, check out the link at the home page of @accelerator account

Check out some of my Prior Posts