Let us start by considering the following word problem from about primary 5 (grade 5) level in Singapore. You may want to have a go at it, just to get a better grasp at what I am going to discuss. Do not worry about whether or you can solve it, as I will reveal the solution later. The whole point of this article is about communication and sense-making for mathermatics teachers and pupils.
The Word Problem

The Teacher’s Marking
The following is from the parent of a pupil who was trying to solve the word problem with bar-diagrams. The diagram was almost correct, but the pupil should have labelled the diagram with words like “Malay” and “Indian”, or with their abbreviations “M” and “I”. [ Aside: The Chinese, Malay and Indian form the largest ethnic groups in Singapore, and there are other people like Eurasians and nowadays Filipinos, plus lots of migrant workers. ]
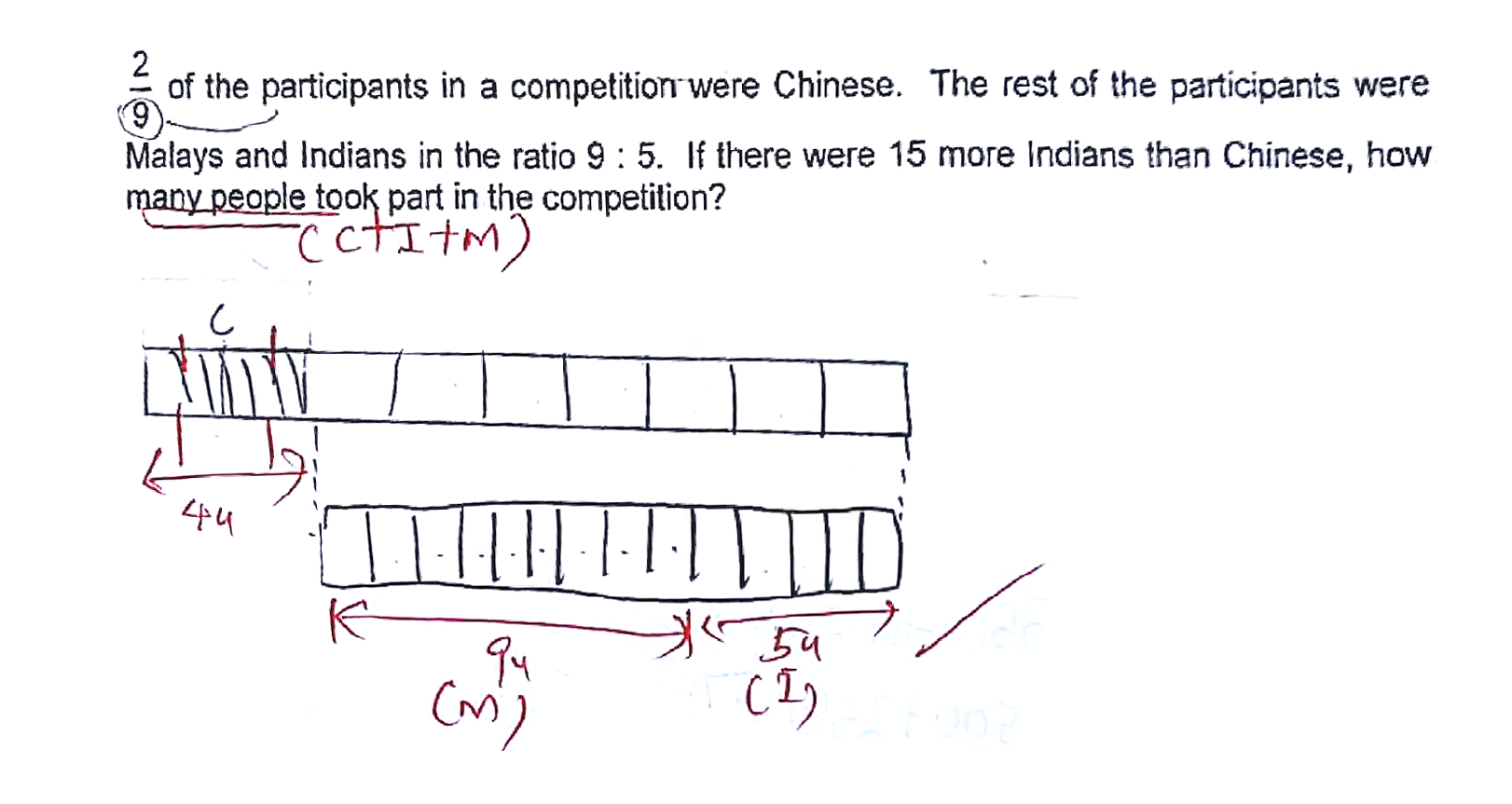
Note that the teacher wrote “4u” (for 4 units) for the bars representing the Chinese. The dutiful parent, who was trying to help the child, was confused. The fraction pertaining to the Chinese is 2/9, that is 2 out of 9, so shouldn’t it be 2 units instead of 4? Why 4?
Yea, why? Think for a moment.
Understanding the Question with Bar-Models
OK, let me explain by showing how I would solve it, using their flavour of bar-diagramming (which tastes a little “algebraic”, with their use of the letter “u”).
First, I start off by reading the question carefully and make sense of it by putting down all the information in a diagram form like this:-
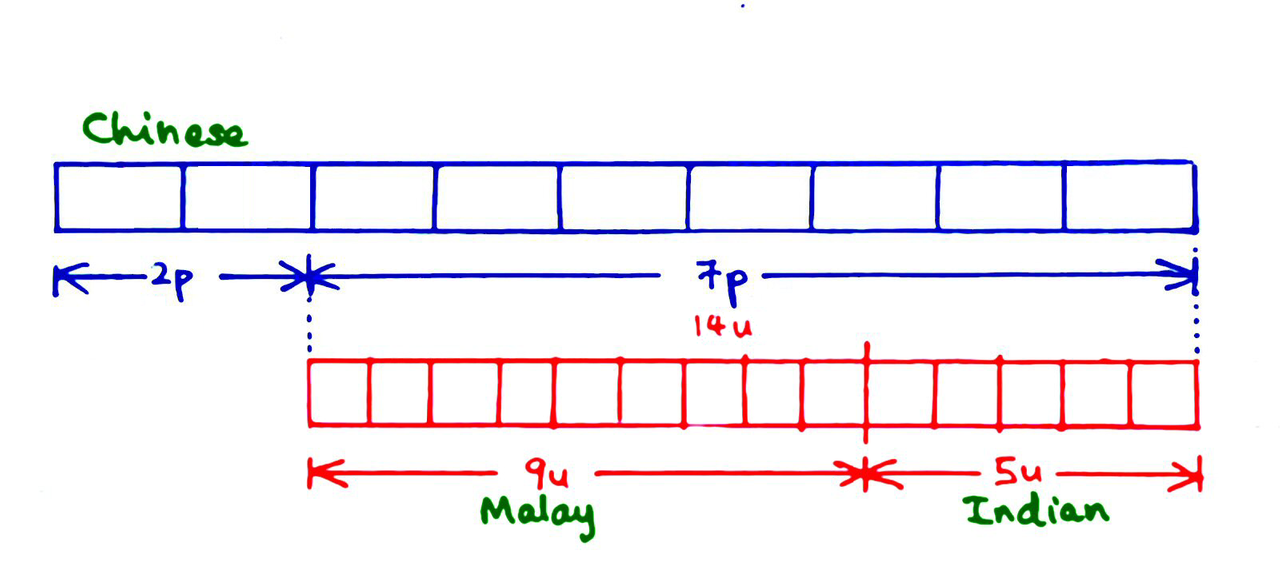
I start by assigning 2 bars (2 “parts” or “2p”) to the Chinese. The others constitute 7 “parts” or 7p, represented by 7 bars. All these will be in pencil, but I use blue to highlight my sense-making of the first sentence, and green to make the labelling of the racial groups stand out. After reading the second sentence, I draw 9 “units” or 9u for the Malays and 5 “units” or 5u for the Indians. We tend to use different words like “parts” and “units” because the bars are of different sizes and we do not want to get confused between them. There is a total of 14 “units” for the Malays and the Indians (all shown in red here), corresponding to 7 “parts”. So we get the idea that 1 “part” corresponds to 2 “units”. So let us subdivide each “part” into 2 “units”, especially for the Chinese.
The Full Bar-Model Solution (as it should be)
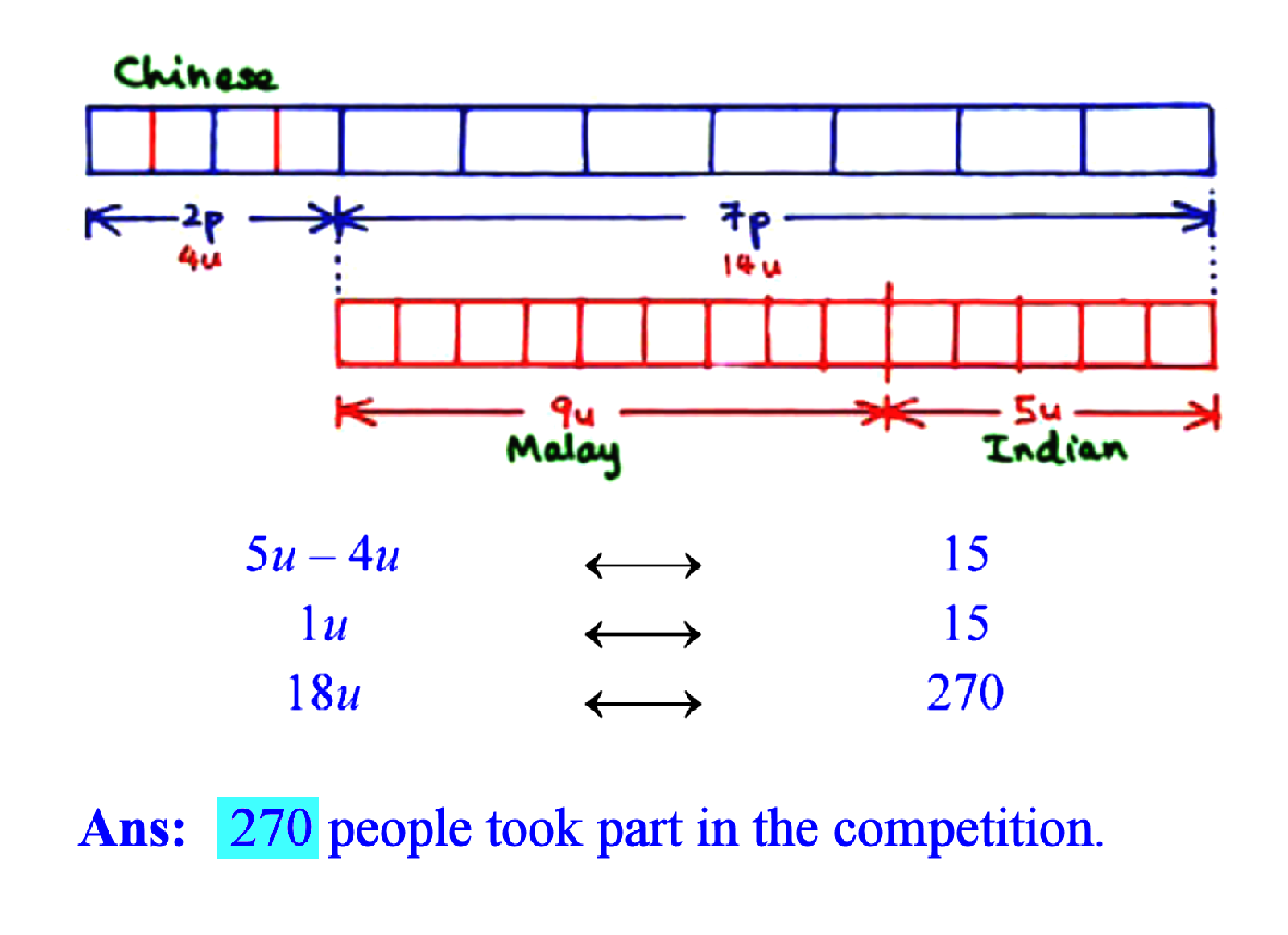
As you can see, the original 2 “parts” for the Chinese has become 4 “units”. That is where the teacher's 4 units came from. Now all our “units” are of the same size and we can meaningfully compare them. The problem now becomes easy to solve. We know that the difference between 5 “units” and 4 “units” (i.e. 1 “unit”) is 15. So 18 “units” is 270. And that is our answer.
Why Clear Communication is Necessary
It is hard to teach sense-making. A lot of it is caught rather than taught. It takes time also to digest and really understand and internalise mathematical reasoning. There are so many questions to go through, but so little time. And teachers might be worried: “And the exams are coming. Oh dear!” I think pupils learn better studying one problem in depth than discussing 10 questions superficially. That is because they are not really learning anything the latter case. The time “learning” would mostly be wasted anyway.
Some teachers may resort to teaching to the test. It is actually just rote learning. Instead of blindly memorising facts, pupils half-wittedly memorise methods of solution. “This is just a method” ... “When you see this sort of question, you do it this way”. This becomes a knee-jerk response. Just follow the d*rn steps. Don’t worry about understanding. This strategy may seem to work for a while, but in the long run it does not. Doing it this way, pupils do not cultivate the right skills, habits and attitudes that would be good for them throughout their life. AFAIK, Singapore’s Ministry of Education does not condone this sort of teaching and learning.
The folks at the ministry headquarters keep setting harder and novel questions fpr the Primary School Leaving Examination (PSLE). Teachers and pupils using rote learning (even the rote learning of fixed methods) will be caught off-guard.
So, what is the antidote to rote learning? It is to help pupils to understand and make-sense of the solution (whether or not they manage to solve the problem). To do that, clear communication is necessary. That is why it is good to make the thinking process clear by distinguishing the “parts” and “units” (or using some other way of distinguishing them). According to Lev Vygotsky, the great Belarussian psychologist, pupils learn things twice: they first from the social plane, and then in their inner mind. Thus teachers, by modelling clear communication to pupils and encouraging the same during pupil-to-pupil interactions, help pupils internalise their thinking more clearly (having clear conversations with themselves inside their minds).
Bar Diagramming : The Good, The Bad and The Ugly
As for bar diagrams, I have this to say: it is a good and powerful method for visualisation and learning, especially for pupils in the lower grades (grades 1 to 4). In the upper primary levels, as the numbers get larger and larger, the number of bars to draw gets larger. It becomes increasingly harder to draw the different bars. Some tutors and authors invent generalised bars where, for example, instead of physically subdividing into 9 bars, they would just draw one bar and write a “9” or “9u” on it. Sometimes you do not know how the bars would fit, and if you get it wrong, you would waste time erasing the pencil drawings. This is not so good if in a test or exam situation. Woe to them that use pens in their diagrams, as these are hard to erase! Sometimes, you do not even know how many bars to draw, as the number of bars is unknown and that unknown number is exactly what the problem wants you to solve for.
Bar diagramming is one of the many tools for problem-solving. It is a good tool for learning, but it should not be worshipped. It should facilitate the problem-solving process. It should not replace the original word problem to become the problem itself.
An Alternative Solution without Bar Diagrams
There are many different flavours to bar-diagramming and alternative presentations. There is even the “Sakamoto method”. I illustrate below, how I would solve the above word problem, using my Distinguised Ratio Units (DRU) form of presentation. I “DRU” the diagram for you below here, and hopefully you will "DRUUUUL" over it.
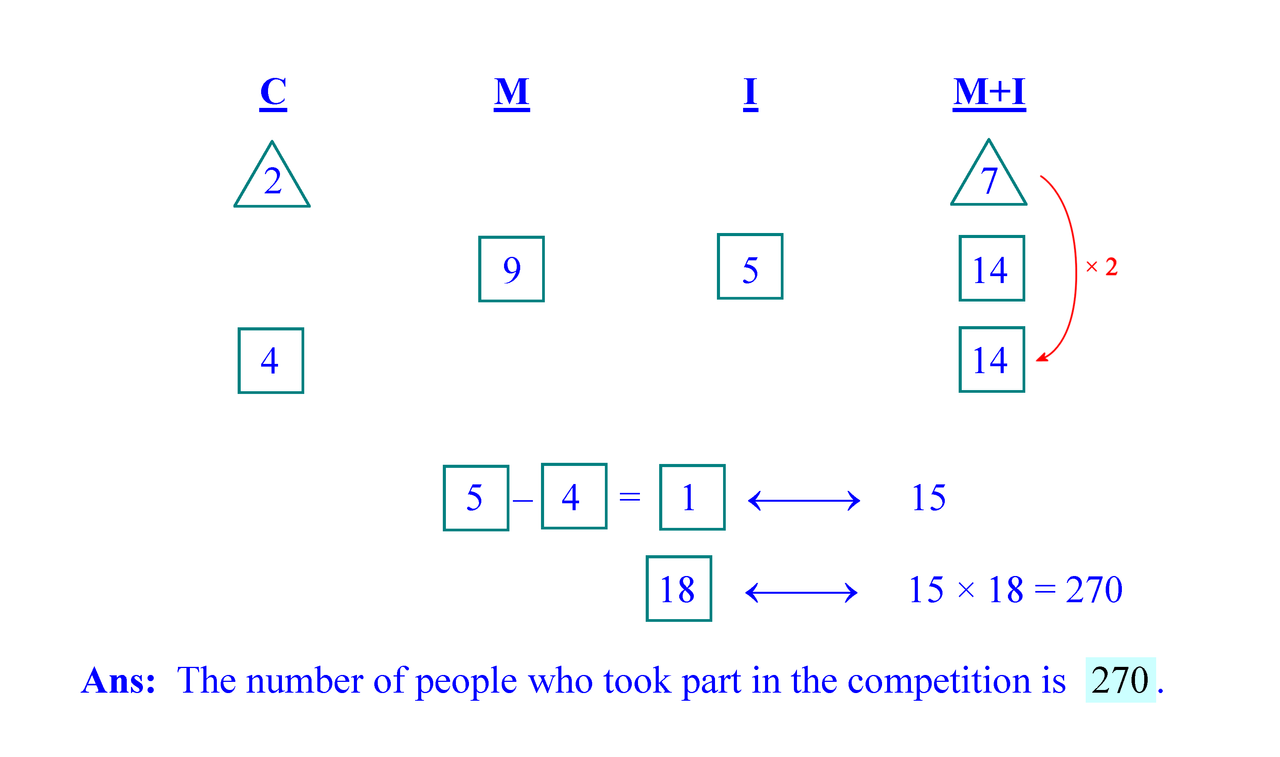
I used 2 “triangle” ratio units for the Chinese and 7 “triangle” units for the other two races (see row 1). In row 2, I have 9 “square” units the Malays and 5 “square” units for the Indians, giving a total of 14 “square” units. To equalise the units, I multiply all the numbers from row 1 to get row 3, where you see 4 “square” units for the Chinese and the matching 14 “square” units for the Malays and Indians. So now I can compare the “square” units and deduce that 1 “square” unit represents 15 (people). So 18 “square” units represents 270 (people). If you compare my solution to the bar diagram solution, you can see that they are sort of isomorphic. The “triangles” correspond to the “parts” in the bar model and the “squares” correspond to the “units” of the bar model. Nevertheless, you do not need to draw so many bars, subdivide them, worry about how they match up, or waste time re-drawing the diagram if you make a mistake.
I hope you have learned something useful. Teachers and students: remember to communicate clearly with one another and with yourselves. This would improve your thinking, and hopefully raise the level of human consciousness in the whole world.
Cheers!
