
In The Sharp Mathematics Contest #1, the following puzzle was posed:-
The Puzzle
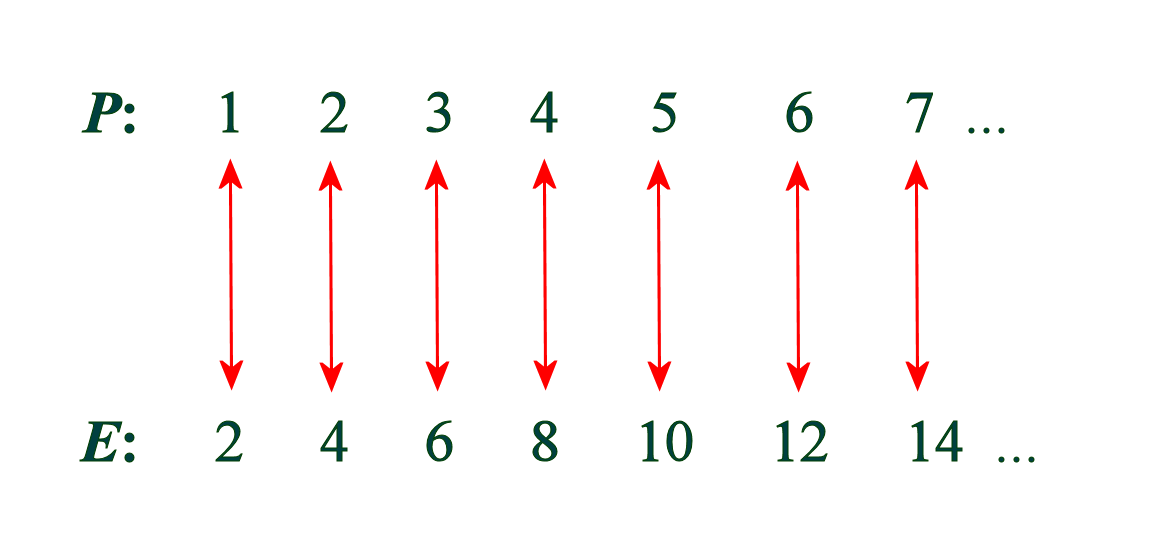
Alice and Betty are arguing over the set P of all positive whole numbers, and the set E of all positive even numbers.
Alice says: "P has more numbers than E, because for example, 3 is in the set P, but it is not in set E."
Betty says: "No! P has the same number of elements as E. The elements in P can be paired up with the elements in E."
Alice says: "But but but but but E contains only numbers like 2, 4, 6, 8, 10, 12, 14, and the number 3 is not in there, whereas P contains numbers like 1, 2, 3, 4, 5, 6, 7, 8, 9, blah blah blah to 14, so P has more elements."
Betty says: "No! No! No! No! No! The blah blah blah goes on forever. Do you see the three dots (...) thingy? the ellipses for both sets? Every positive whole number can be paired with a positive even number by multiplying with 2 ... So P and E has the same number of elements."
Who is / are correct? Can you explain how / why?
Comments on Participation
Although there were numerous upvotes to the contest, only two people submitted (proper) entries, and there are 3 prizes. So both participants get the first two prizes! You guys left the third prize (2 SBD) on the table.
@beachhermit basically said Betty was correct but Alice was wrong, gave some good illustrations and intuitive arguments. Also did research about "infinity" and included stuff not asked for (this won't be penalised).
@resorus says both are the same because both are infinite. Er ... actually there are many types of infinity! "But infinity is not a number!" ... not a number like our whole numbers. However, there are different infinite cardinal numbers e.g. aleph null which is "countable infinity", and continuum a type of "uncountable infinity". There are countable infinity and uncountable infinities. In fact, there are uncountably infinitely infinite infinities of different types!!
@beachhermit's answer is better. So ...
the 2nd prize (3 SBD) goes to @resorus
the 1st prize (5 SBD) goes to
(drum roll) ...
@beachhermit !!!
Ta da!
My "model answer", or maybe just answer that I would have love to have received, is here.
Announcements
My recent digest of articles is here.
If you find my articles useful or interesting, please upvote and resteem them! Thanks you very much!
Follow me and watch out for more Sharp Mathematics Contests!
@tradersharpe
-- promoting sharp minds
P.S. Contest #2 is here.
