This article my "model answer" to my "Sharp Mathematics Contest #1", which is a modified version of Galilei's Paradox comparing the set of positive integers with the set of even positive integers.
The Historical Context
Galileo Galilei was famous for getting into trouble when he challenged the Roman Catholic Church's authority regarding the issue of whether the Sun revolves around the Earth. He purportedly dropped two objects of different masses down the Leaning Tower of Pisa to prove that objects fall at the same rate due to gravity regardless of their masses. Not many people know about the Paradox of Infinity that is named after him.
When I look at the contestants' answers and some other articles, it seems that people nowadays have been exposed to the idea of using the concept of pairing up (1-to-1 correspondence) for infinite sets (Betty's point of view) while under-appreciating the other concept, namely that of proper subset inclusion (Alice's point of view). It would appear that people just parrot ideas that have been repeatedly promulgated in the popular media. I think people need to be more critical, or at least have a deeper understanding of the issues involved, otherwise they can become easily fooled and manipulated by the media in other areas such as economics, politics and geopolitics that also affect our lives. Like in the story of the Blind Men and the Elephant, each of the different blind men can be correct from his perspective, although he may not have the full picture.
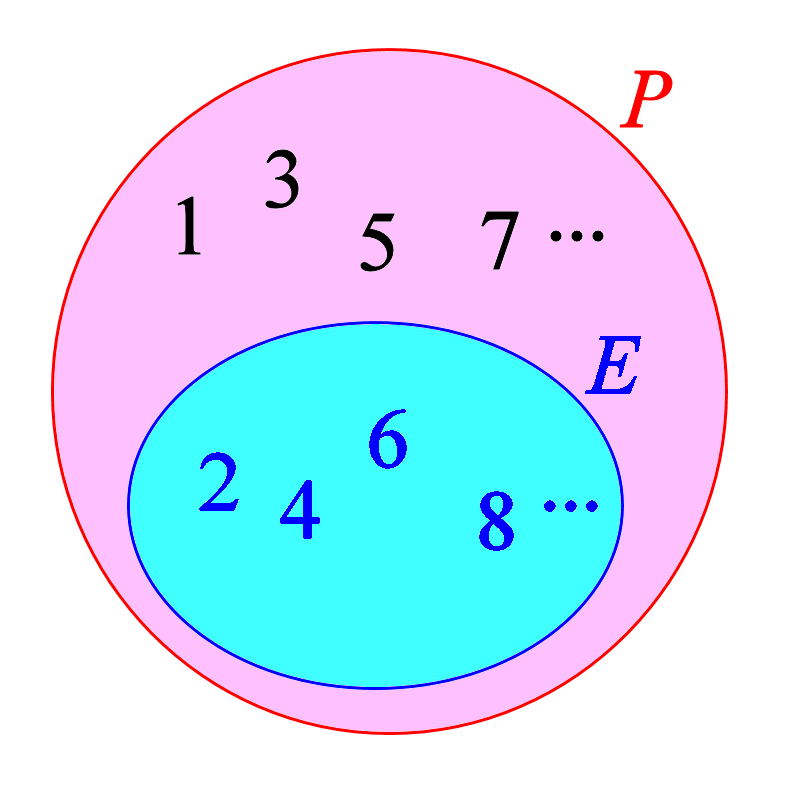
Perhaps it was my fault for showing only Betty's point of view. I should have given the diagram below to do justice for Alice's point of view.

The set E of positive even integers does indeed appear to be smaller than the set P of all integers. There are so many elements, infinitely many elements in fact, that are in P but not in E.
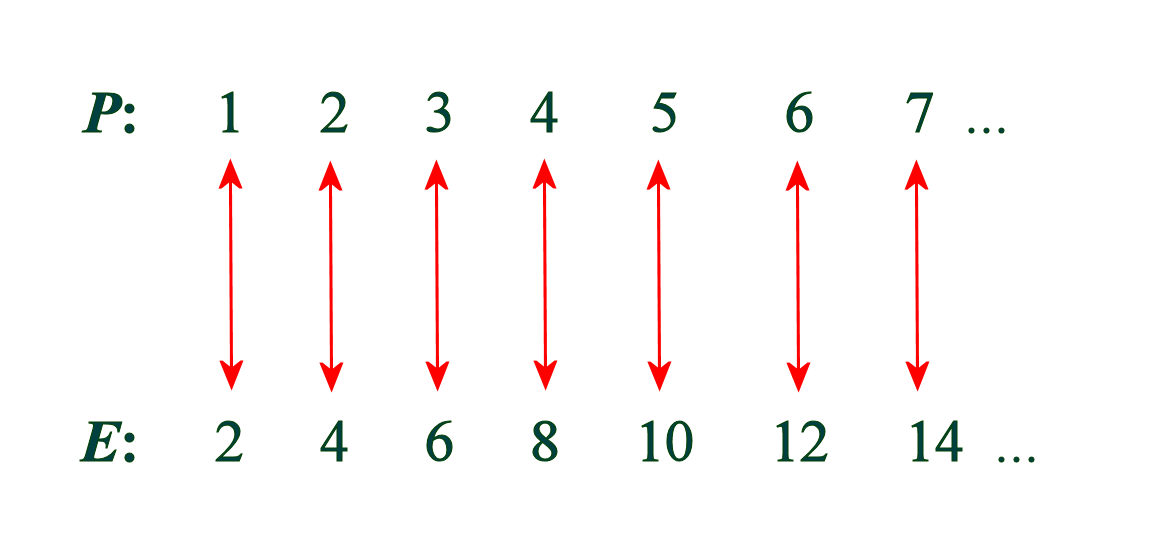
To appreciate the nature of the problem even better, let us look at the original "Galileo's paradox". In the original version of the paradox, the set of positive integers was compared with the set S of perfect squares, or square numbers, namely the numbers
1² = 1×1 = 1,
2² = 2×2 = 4,
3² = 3×3 = 9,
4² = 4×4 = 16,
... and so on.
You can pair off the positive integers (P) with the square numbers (S) like this:-
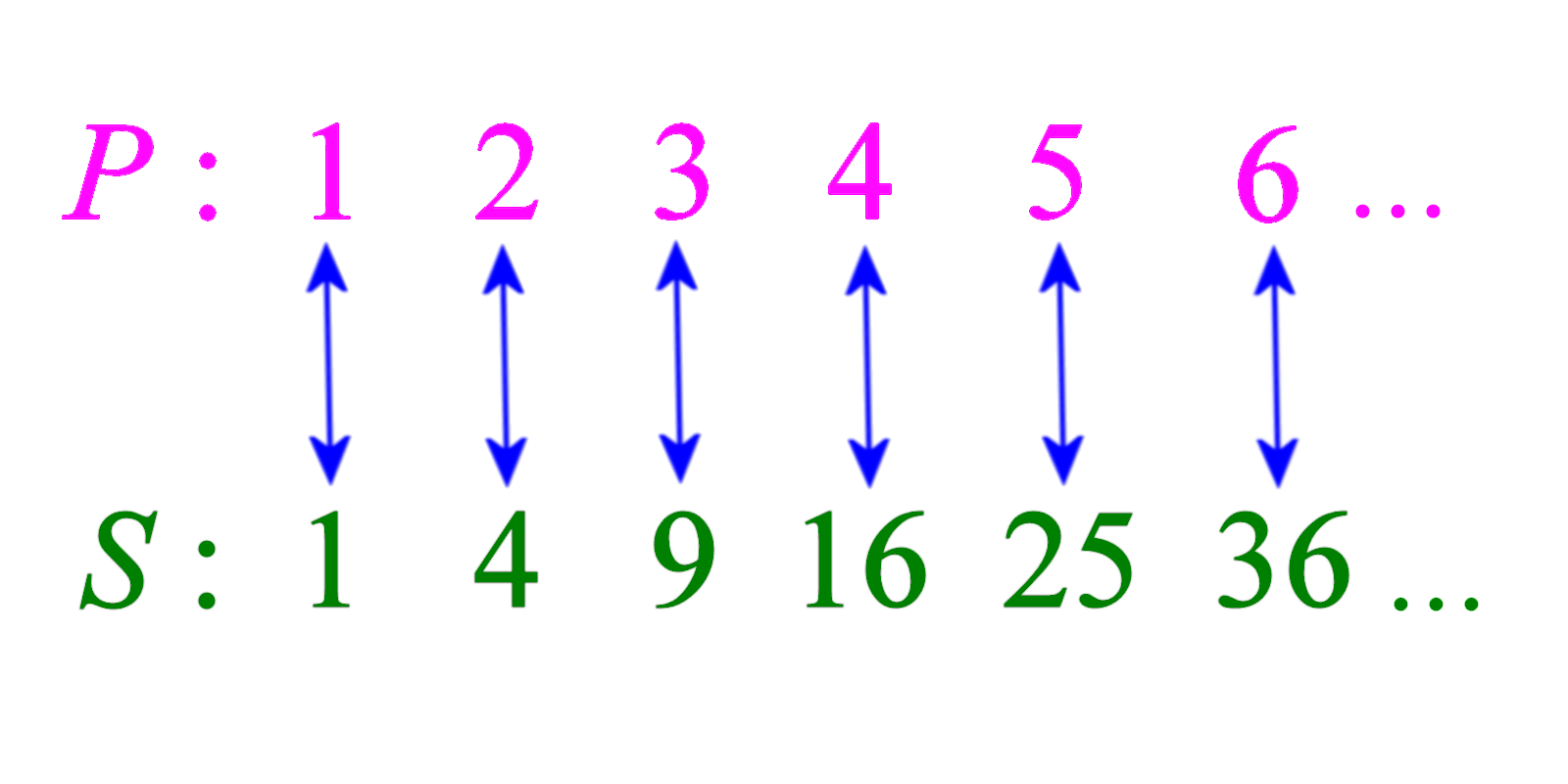
You can view the square numbers (S) as a proper subset of the positive integers (P) like this:-
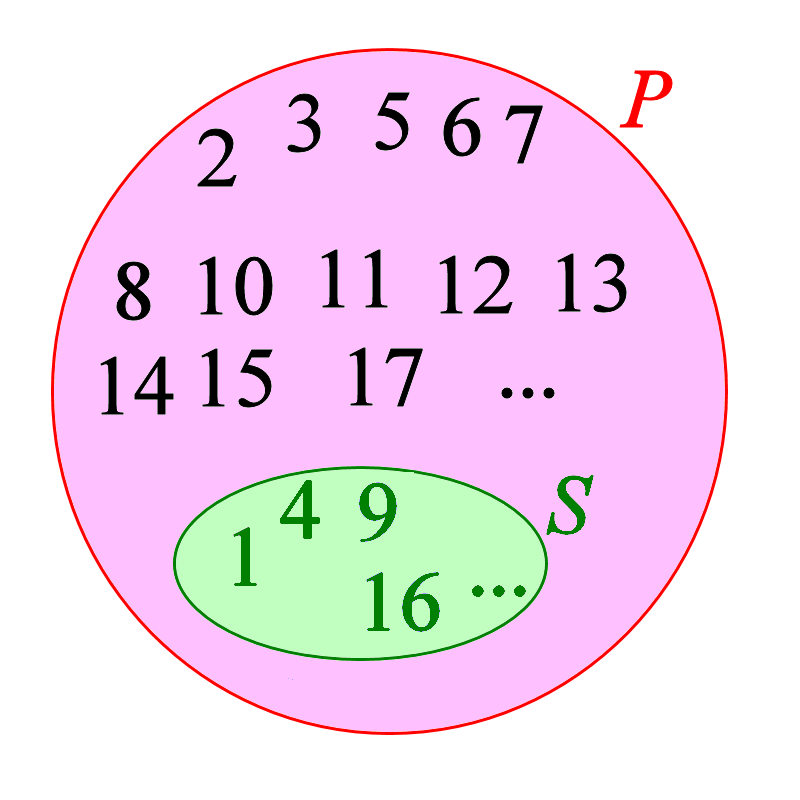
This looks even stranger than the Alice and Betty dispute. It seems that there are vastly fewer perfect squares (e.g. 1, 4, 9, 16) than the positive integers and yet, paradoxically, the two sets can be paired on a 1-to-1 basis.
If we compare both Alice's and Betty's points of view, we will see that both of them do have a point. Betty is correct, in a way. Alice is also correct, in a way. So both are correct, in some sense, and yet they apparently contradict each other. Do you really understand the problem now? This paradox is not easy actually! It stumped mathematicians for at least four centuries! Mathematicians are among the smartest people on earth. So if they get stumped, it was really difficult! I did not mention this in the contest because I did not want to discourage people from trying. ;-) If you don't tell people that it is difficult, they might not "know" that it is difficult, and maybe someone might just come up with some brilliant answer. Who knows? Anyway ...
The paradox was cracked due to the genius of Georg Cantor, who came up with his theory of infinite sets. He clarified many concepts, including the concept of "same number" via bijection or "pairing up". During his day, his ideas were not so popularly accepted, unlike today. He actually became mentally ill because of rejection by other mathematicians. Today, he is regarded as one of the most brilliant mathematicians.
So how was the paradox resolved? In an earlier article, I said that clear communication and sense-making is very important in mathematics. If our communication is unclear, then our thinking (self-communication) will be unclear. It is often the case that mathematical paradoxes are due to a lack of clarity in our communication and thinking, rather than a real contradiction.
We need to clarify two concepts:
(1) what do we mean by "proper subset"
(2) what do we mean by "less than".
Are they always mean the same? Or when are they the same and when are they different?
Concept 1 : Proper Subset
The set A is a subset of B, written , means
"every member/element of A is a member/element of B".
The set A is a proper subset of B, means but
. More explicitly, we define

According to this definition, the set E of even positive integers is definitely a proper subset of the set P of positive integers. So in this sense, Alice is correct.
Concept 2 : Less (in cardinality) than
The cardinality of a set is the "number of elements" in a set. It is the property that is preserved by bijections. In other words, the cardinality or "number of elements" in a set is that property which is unchanged under a one-for-one exchange of any or all of the elements, as explained in my an earlier article.
For example, the cardinality of {x, y, z} is 3. We can extend the concept to infinite sets. The cardinality of the set of positive integers is
("aleph null"), which is the lowest form of infinity. The cardinality of the set of even positive integers is also
. There are higher infinities (e.g. the "continuum") and infinitely infintely many infinities!! This will blow your mind if you try to think about it!
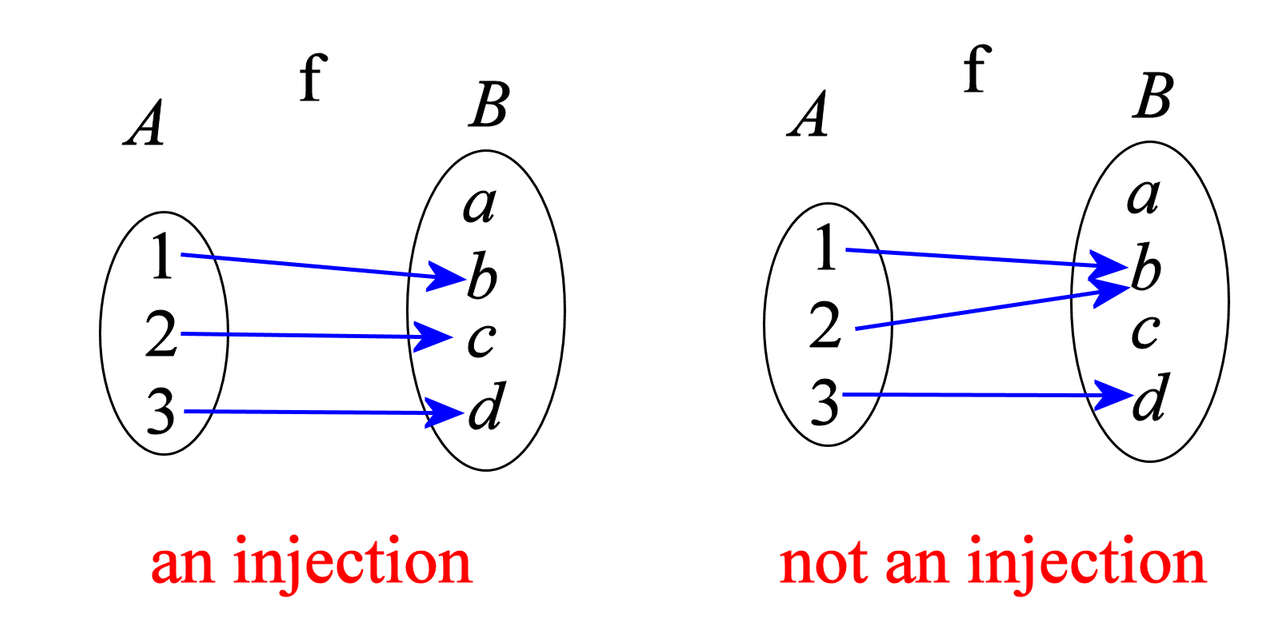
So what do we understand by "bijection"? A bijection is a function or mapping that is both an "injection" and a "surjection", So we need to understand what is an "injection" and a "surjection"
The function f mapping from set A to set B is an injection (a.k.a. "injective function" or "1-to-1 function") means different members of A map to different members of B. There are no syringe and needles involved here, so don't worry. But you cannot have two different elements from A mapping to the same element in B.
The function f mapping from set A to set B is an surjection (a.k.a. "surjective function" or "onto function") means for every element b of B, there is at least one element a from A such that f(a) = b.
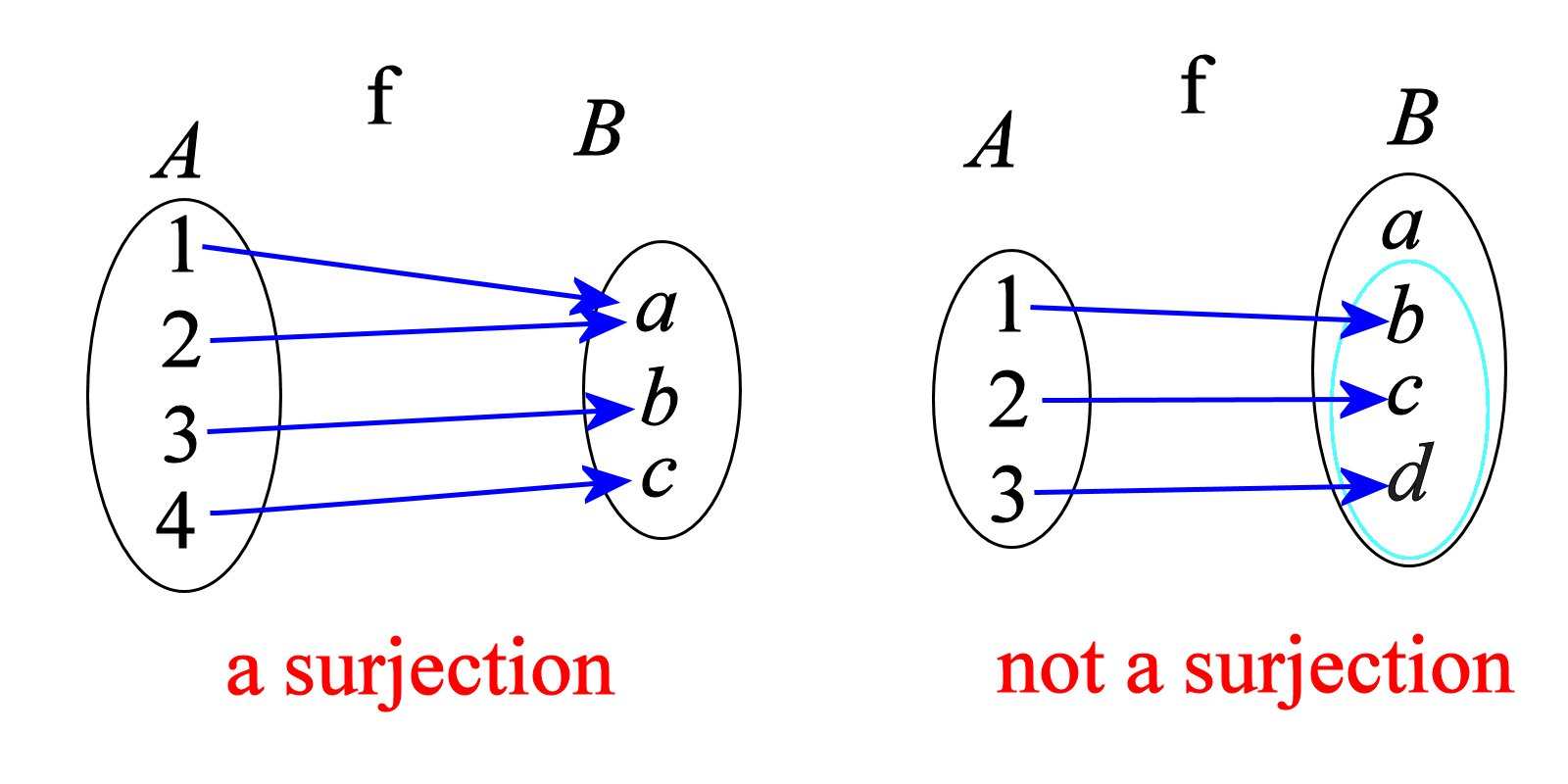
In the example on the right half, the element a of B does not have a "partner" from set A that links to it. In a surjective function from A to B, every member of B must have at least a "partner" from set A. Yes, they can share partners. ;-) But no lonely members are allowed in set B ;-)
The function f mapping from set A to set B is a bijection (a.k.a. "bijective function" or "one-to-one correspondence") means it is both an injection and a surjection. Every element from A is linked with one and only one element from B and vice versa.
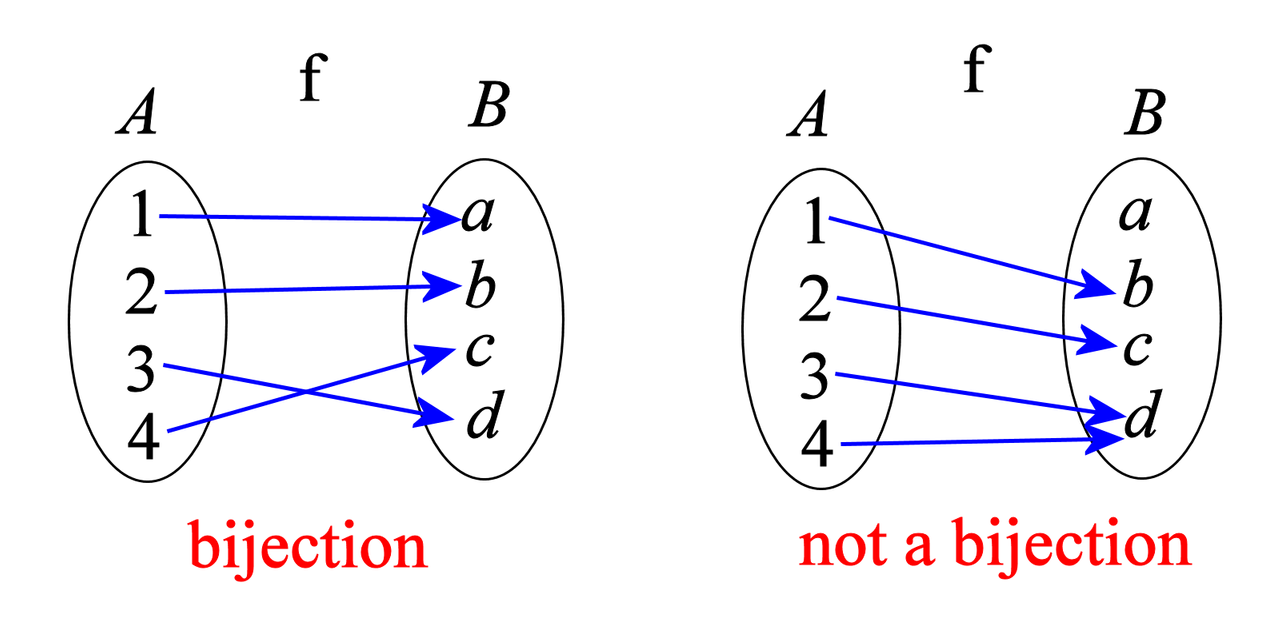
A bijection must not have two (or more) elements linking to one element, and/or any "lonely hearts", as in the example on the right half.
Two sets A and B are equipollent (or equinumerous or "have the same number of elements" or "have the same cardinality") means there exists at least one bijection between the two sets. In other words it is possible to link them up via some bijective function. There may be more than one way to pair up the elements, but there is at least one way to do so. I shall denote this by . In terms of "same cardinality", we may also denote this by |A| = |B| or Card(A) = Card(B).
According to this definition, the set E of even positive integers is equinumerous with the set P of positive integers. We can set up a function f from E to P with the rule , obviously a bijection whose inverse function has the rule
. So in this sense, Betty is correct.
Now, what do we mean when we say that set A is numerically "less than" B?

OK, now so what?
Well, it can be proven (via a Mathematical Induction or related type of argument) that if A is a subset of B and if B is a finite set, then the two concepts are logically equivalent. If one is true, the other will be true. They mean the same in the finite case. Although there are infinitely many finite positive integers, and Mathematical Induction can be used.

If B is infinite, then we cannot use the Mathematical Induction argument. Instead, we can find examples where A is a proper subset and yet can map bijectively with B. The Alice-Betty dispute and the original Galileo's Paradox such examples.
TL;DR
To sum up, it turns out that there are two different concepts:
(1) "proper subset" and (2) "less (in cardinality) than". These two concepts are "fused" together in the finite case, but they are different in the infinite case. Mathematicians had mistakenly assumed that what worked in the finite case transferred over to the infinite case. The two concepts are why infinite is different from finite. "Infinite" means "not finite". So it has different characteristics. That's precisely why it is called "infinite"! Therein lies the intrigue!
In this article I have
(1) told the story behind the puzzle (the historical context)
(2) explained where the difficulty lay
(3) reinforced the need for clear communication and definitions
(4) explained the two key concepts at the centre of the paradox
(5) shown the circumstances under which they are the same and
not the same
This article is not a mere "copy, paste and modify" type of article with some dressing up by outsourced graphics. All the diagrams in this article are my own original work!
Hope you all like this!
Announcements
The winners to The Sharp Mathematics Contest #1 are announced here.
My recent digest of articles is here.
If you find my articles useful or interesting, please upvote and resteem them! Thanks you very much!
@tradersharpe
-- promoting sharp minds
