Learn how to derive the energy levels of a Hydrogen atom from scratch in 6 easy steps. It is a beautiful demonstration that reminds us that art and science are really not so far apart!

By posing his model of the hydrogen atom (an electron in circular motion around a proton), Niels Bohr was able to predict the existence of emission and absorption spectra. The video in this post will show you how he did it by proposing that the angular momentum of the electron was quantized, and how he ends up with this famous equation for energy levels permitted in the Hydrogen atom:
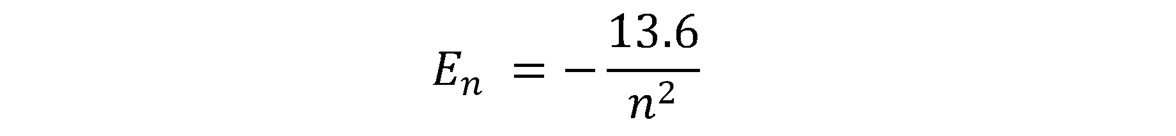
The first video of this series discusses the energy of an atom within the scope of the model defined by Niels Bohr. Such model describes an atom as being a nucleus around which electrons are in circular orbit. This is the model used for the whole series as an introduction to the amazing world of quantum mechanics. The second video describes light as both being a localized wave and a particle, but most importantly, it explains that light is made of quanta of energy (fixed amounts of energy) called photons. The size of the quanta of energy of a given light defines the color of that light. The third video showed us that the energy of an atom can only exhibit certain values, in other words, the energy of an atom is quantized. This is why it is said that an atom has levels of energy. In this episode we will work out from scratch Bohr's formula. Click on the video below to enjoy that fascinating voyage deep inside the atom.

The six steps
Step 1: Express mathematically the energy of the electron (which is also that of the atom) using Newtonian mechanics.
Step 2: Realize that because the electron is in circular motion, the coulomb force between proton and electron is a centripetal force.
Step 3: Rearrange the resulting equation to show that the total energy of the electron only depends on the radius of its circular motion (R).
Step 4: Apply Bohr's proposition to quantize the angular momentum, and then combine it with the equation obtained in step 2.
Step 5: Rearrange that combination to express R with universal constants only and the quantum number n introduced in step 4.
Step 6: Inject this expression of R into the equation for the total energy of the electron obtained in step 3. The energy (in Joules) will only depend on n. Divide by 1.6 x 10^-19 to get it in eV and obtain Bohr's famous expression.

This video series is aimed at providing an introduction to the quantum world to non-scientists and high school students preparing for their high school exams.
If you wish to deepen your understanding, please explore @lemouth quantum mechanics series. The relevant chapter to this specific video is:
Quantum mechanics lessons on Steemit - 10 - the Bohr model of the atom
Image credit: the frieze was created using an image found on Pixabay.com

Hi,
I’m @muphy,
My life revolves around music production, teaching sciences, and discovery through travel.
You enjoyed that post? Resteem and Upvote!
You are interested in these topics? Follow me!

