
In my last quantum mechanics post, I introduced the planetary model of the atom that was proposed by Rutherford at the beginning of the 20th century. I also explained, at the end of the post, why it was not working.
Another model explaining the observations was therefore needed. We had to wait until 1913 to get an attempt proposed by Bohr. Before moving on with the topic, it is useful to go back to a few key notions.
MOMENTUM
The momentum is the first of these notions I would like to highlight.
In classical mechanics, the momentum is defined by the product of the mass of an object and its velocity. It is thus a quantity involving mass and motion, and it often matches the concept of quantity of motion.
The quantity of motion is however different, in particular when electromagnetic fields are into the game. Without field, the two are actually the same.
The notion of momentum is crucial because it is a conserved quantity, as pointed out in the 17th century first by Wallis and then by Newton. In other words, no matter whatever is happening to a given (closed) system, its momentum does not vary.

[image credits: Wikipedia]
For instance, if two particles A and B collide and get transformed into two particles C and D, the sum of the momenta of A and B equals the sum of the momenta of C and D.
It works the same with a pool cue transferring its momentum to the balls, as in the image.
The momentum can also be used to cast the second law of Newton: the rate of variation in the momentum of a system gives the force acting on it. Momentum is indeed conserved: if it varies, there must be an effect compensating the change.
In this section, I have tried to highlight the importance of the momentum in physics. This quantity is very important and can help solving many problems.
But the story does not end here: this notion can be generalized in the context of rotations.
ANGULAR MOMENTUM
I have so far not discussed rotations, and more in particular systems in rotation (like a compass or a gyroscope). However, systems in rotation are important, in particular for the context of an atom whose electrons are orbiting around a nucleus.

[image credits: Wikipedia]
But before going down in size towards the atom, it is good to focus on something bigger, like a gyroscope (on the picture).
The angular momentum still involves the notion of mass and displacement, but this it also involves this time the notion of position.
It is useful to start with a definition. The angular momentum (L) defined as the cross product of the position (r) and the momentum (p),
L = r x p where the momentum p = m v.
Here Bold-faced symbols denote vectors.
Yep, sometimes equations cannot be avoided… As well as weird formulations: the angular momentum is the moment of the momentum.
Moreover, as the momentum, the angular momentum is a conserved quantity and thus a useful concept for solving many problems in physics when bodies in rotation are involved (e.g., from gyroscopes to neutron stars!).
QUANTIZATION OF THE ANGULAR MOMENTUM
It is now time to go straight to the topic. One could easily calculate the angular momentum of an electron orbiting around the nucleus of an atom.
The magnitude of this vector directly stems from its definition:
L = me r v
It is given by the product of the mass of the electron, its position and its velocity. Taking a hydrogen atom, electrons can orbit at different distances from the nucleus (different values for r) and with different speeds (different values for v).
But what does the model of Bohr say about this. It actually says two important things, starting from the fact that as in the planetary model of the atom, electrons move on circular orbits:
- The angular momentum of the electron is quantized and can only take as values an integer number of times Planck constant.
- When the electron orbits around the nucleus, it does not radiate. Emissions are only related to a change in the orbit radius.
EXPLANATIONS
The two assumptions behind the model of Bohr have deep implications. Let us take the hydrogen atom for concreteness.
[image credits: UNL]
First, the angular momentum of the electron can only take values belonging to a given set. Once the Planck constant, twice the Planck constant, etc. I generality, n times Planck constant. This n number will come back below and is important.
Second, the way in which the electron can lose energy is to move from one orbit to another orbit, and this results to a photon emission. The energy is conserved, so that the energy difference between the two orbits is the one carried by the emitted photon.
There is no classical physics argument that can demonstrate these postulates.
From there, calculations can be made and the energy of the electron is given by the formula on the left.
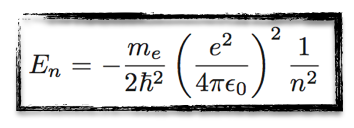
[image credits: homemade]
Sorry for the details, but I skip them for brevity.
Fr those interested, we start from the expression of L for a given orbit and the expression of the orbit radius as derived from Newton’s fundamental principle of dynamics. We then derive the expression of the electron radius and velocity in terms of n, and gets straightforwardly the expression for the energy.
In the final result, the n index is the same n as above. Once n is fixed, the orbit radius, the electron velocity and the energy level are all fixed.
DISCUSSION AND REFERENCES
In the Bohr model, the quantization of the angular momentum leads to the quantization of the energy levels of the hydrogen atom. The energy can only take discrete values.
By studying the energy differences between two levels, one can trace back the energy possibly carried by photons emitted by hydrogen atoms.
If you remember some old post I wrote, I introduced the Rydberg constant. This constant is a property of the atomic spectra of the atoms (and thus of photons radiated off atoms), and one of the nice feature of the Bohr model is that it shows that the Rydberg constant is not fundamental but connected to other fundamental constants.
However, when we try to explain other atoms with the Bohr model… it fails (that is already the case for helium). There are thus shortcomings in the model, and the theory that will solve them all is … quantum mechanics. But this is the topic of the next posts.
For more information (and references), one can check either this book, or the wikipedia page on the momentum, the wikipedia page on the angular momentum and the wikipedia page on the Bohr model.
Table of contents of this series of posts
I. Introduction
1. Concepts and fundations
2. Interactions and conservation laws
3. Systems of particles
II. The origins of quantum mechanics
1. Fundamental physics at the beginning of the 20th century
2. The mysteries of the atomic spectra
3. The mysteries of the black bodies
4. Quantization of the electromagnetic radiation and the birth of the photons
5. The Compton effect
6. The planetary model of the atom
7. The Bohr model of the atom (this post)
For more discussion on this topic (or anything related to science), please join us on #steemSTEM. The steemSTEM project is a community-supported project aiming to increase the quality and the visibility of STEM (STEM is the acronym for Science, Technology, Engineering and Mathematics) articles on Steemit.
More information on our actions are available here. You can also follow our curation trail on Streemian to support us (or by chatting with us on the chat if you do not wish to use Streemian).
