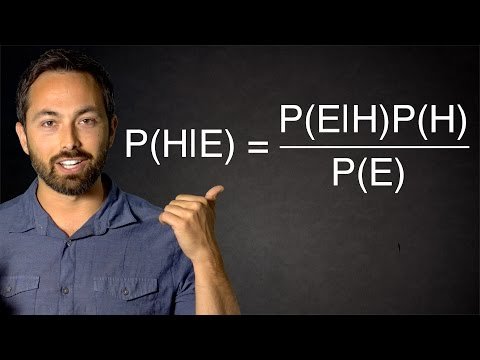What is the "Bayes' Theorem"?
"Bayes' theorem is a mathematical formula for determining conditional probability named after 18th-century British mathematician Thomas Bayes (1701–1761). The theorem provides a way to revise existing predictions or theories given new or additional evidence. "
It was further developed by Pierre-Simon Laplace, who first published the modern formulation in his 1812 “Théorie analytique des probabilités.” Sir Harold Jeffreys put Bayes’ algorithm and Laplace's formulation on an axiomatic basis. Jeffreys wrote that Bayes’ theorem “is to the theory of probability what the Pythagorean theorem is to geometry.”
Written out the formula looks something like this:

How can we use it?
Let's take a look at some examples of Bayes rule in action.
The Disease Test.
You don't feel so good. After visiting a doctor and taking a test you are diagnosed with a very rare disease that has a likelihood of 1 in 10 000. The test has an accuracy of 98%. So, how probable is it that you have this disease?
It's not 98%.
Let's solve the formula if:
P(E) = P(H)P(E/H)+P(-H)P(E/-H) = 0,0001 * 0,98 + 0,9999 * 0,02 = 0,020096
So the probability of you having the disease after testing positive is actually ~0,5% after crunching the numbers.
An easier way to see it: If from 10 000 people 1 has the disease and the test picks out 200, the chances of you having the disease is 1/201 = ~0,005 =0,5%
Let's take another example
"Imagine there is a drug test that is 98% accurate, meaning 98% of the time it shows a true positive result for someone using the drug and 98% of the time it shows a true negative result for nonusers of the drug. Next, assume 0.5% of people use the drug. If a person selected at random tests positive for the drug, the following calculation can be made to see the probability the person is actually a user of the drug.
(0.98 * 0.005) / ((0.98 * 0.005) + (0.02 * 0.995)) = 0.0049 / (0.0049 + 0.0199) = 19.76% Bayes' theorem shows that even if a person tested positive in this scenario, it is actually much more likely the person is not a user of the drug.Changing how we think in everyday life
Too often do people think they know something 100% or change their minds completely when presented with new evidence.
Bayes' rule helps us with taking on new information and processing it the right way.
We don't need to sit down and use the formula in our every-day lives, that would be counterproductive. Instead there are key points to keep in mind. It's all about probabilistic reasoning.
When you are confronted with new information you need to figure out how much that new evidence will change your current belief. There is no black and white. Your beliefs can change indefinitely.
But how do you make up the rules of evidence? How will you know the value of any evidence?
You don't. The rules are ever changing and subjective.
Let's say you believe morning yoga will make you a happier person. After doing yoga for a while you are feeling happy about 3 days from 7. What if before you did yoga the results were the same? This isn't strong evidence. But for someone that is feeling bad constantly the evidence is very strong that yoga will make you happier.
If you are presented with new evidence revise your prior evidence. For example if you go home late at night and someone is "apparently" following you. How likely is it that this person is someone with ill intent? While the initial reaction can come off as strong evidence, you'll quickly realize on average there aren't many bad people and it's much more likely he just shares a similar way home.
Evidence can also be wrong. You should never dismiss evidence nor should you change your belief, but update your amount of belief incrementally.
People often tend to make wrong assessments. They'll use irrelevant data or start out with a wrong belief.
Imagine asking your friend for advice on something he has no knowledge in. How common is it for him to still give you advice whether he knows the topic or not? He's advice is irrelevant.
You should never be 100% certain of anything. It means your beliefs are unchangeable even if presented new evidence. You should however say you think something is extremely likely.
To sum it up
...the most important lesson here is that knowing something for sure is highly unlikely. There are too many variables. You should however keep asking questions, challenging your own beliefs and never believing anything.
Useful videos:
Sources:
http://io9.gizmodo.com/how-bayes-rule-can-make-you-a-better-thinker-471233405
https://en.wikipedia.org/wiki/Bayes%27_theorem
http://www.investopedia.com/terms/b/bayes-theorem.asp
http://www.gaussianwaves.com/2013/10/bayes-theorem/
Some of my previous posts!
You can find me on:







Feel free to use my images :)
Questions about photography are welcome!
Upvote, comment, resteem and follow if you like!
Have a great day!