
Ooh! Looking smart! I'm reminded of a quote from the book Betrayal, a comment on the irresistible attraction many women feel toward priests: "Put a Roman collar on a lamp-post and some woman will fall in love with it."
Source: Wikimedia Commons contributors
Intro: 7 chromosomes for 7 characters with 7 notes
It isn't easy to talk freshly about a subject that's taught, not only in all university Biology 101s, but also to all schoolchildren.
But since I don't think a biology tutor ever stood in front of his class to deliver his message in freeform poetic sing-song, let me try, although we'll have to make do without audio. Unless @mobbs is willing to chip in.
Here we go.
[intro] ♪ Gregor Mendel was a Monk who wanted to be a science teacher. 🎹 [cheerful piano] But he royally flunked his certification exam so he went back to being a preacher. 𝄫 [double flat] He was strong-minded though, he never let that failure ruin his comportment ♯ [sharp]. So he made a garden, bred some peas, set up controls, hypothesised, recorded, and lo and behold, the data upholded his Law of Independent Assortment. 𝄞 [beautiful] He was lucky tho that the humble pea had exactly 7 chromosomes, the very number of characteristics he studied ♫ [enter trombones]. An extra A, one more big Y, just one more little b, and the phenotypes would have to inherit in link, and Mendel would have had to have abandoned 𝄇 yes abandoned, that famous law of theoretics, that established him as the father of the science of genetics. ♬ [outro]
Well, that didn't go half as bad as I expected. And I only used 7 notes to play that to you: do re mi fa sol la si.
And now that you got the Cliffs notes of the story down, let's dive into the nitty-gritty.
8 years' research presented on Feb 8 and Mar 8

He was too poor to print his face on paper money, so they made him a stamp.
Source: Wikimedia Commons contributors
As a man born in a family with limited means, Mendel knew the importance of numbers. After 8 Years A Slave of research, he read his paper to the Natural Science Society in Brno on February 8 and March 8 of 1865. [3] (1888 was a long way away.) The paper was not light on numbers and symbols and statistics. I will do my best to do a diet version of it.
In the introductory remarks, Mendel starts off like any self-respecting researcher does, by underscoring the difficulty of the research he conducted, so that everyone will know how hardworking he is:
That, so far, no generally applicable law governing the formation and development of hybrids has been successfully formulated can hardly be wondered at by anyone who is acquainted with the extent of the task. [1]
Neither was the importance of the task left to the imagination:
It requires indeed some courage to undertake a labor of such far-reaching extent; this appears, however, to be the only right way by which we can finally reach the solution of a question the importance of which cannot be overestimated in connection with the history of the evolution of organic forms. [1]
Let the man pat himself on the back: not only did he fail his teacher exams, but he suffered from regular bouts of depression, and, most importantly, his given name Johann was changed to Gregor when he took the cloth [3]. There's only so much a man can bear!
I kid. Mendel is actually 100% right: though experiments with breeding had been done before, no one had yet succeeded in formulating a law of inheritance. Perhaps that was because no one had ever approached the issue as mathematically and statistically and rigorously as Mendel did. The authors of An Introduction to Genetic Analysis, 7th edition [2] put it in no uncertain terms:
Mendel then did something that, more than anything else, marks the birth of modern genetics: he counted.
Italics theirs.
So let's count along, see if the numbers check out. (Spoiler: they don't.)
Counting with Mendel
P: The Parental Generation
After having procured 34 distinct varieties of peas, Mendel grew them, and kept reproducing them and growing them for 2 years to make sure they bred true: meaning, they "exhibited constant and similar offspring". [1]
He chose to study 7 distinct characteristics that lend themselves to clear definitions: seed shape, seed color, flower color, pod shape, pod color, flower position, and stem height.
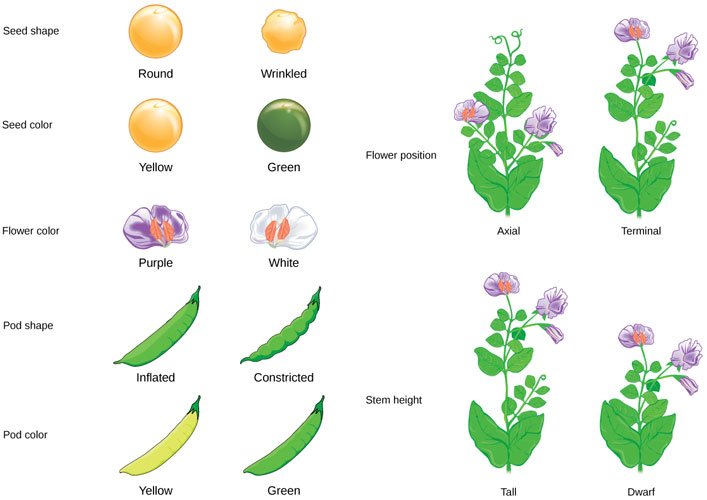
Mendel's 7 musical characters
Source: OpenStax, Principles of Biology
The careful observer will here notice the absence of any intermediates. Where is, one will ask, the medium-length stem? Why is it just tall or dwarf? Why is there no in-between?
This in-between theory has a name, it's called blending inheritance: it's the idea that a white flower crossed to a purple one will give the same result as a purple paint and a white paint mixed together by a painter's brush. As we'll see, Mendel's experiments blew the blending inheritance hypothesis out of the water, probably using a pressurized garden hose.
But if the blending inheritance hypothesis is false, then what determines which characteristic will be expressed from the two alternatives? We'll have to wait for molecular biology to be invented to learn how that works, but for now, Mendel called those characteristics that win the inheritance wars dominant, and the others recessive. They're called recessive instead of 'defeated' or 'dead' because they nevertheless appear entire in the following generations.
As we'll see.
F1: The First Filial Generation
In this generation there reappear, together with the dominant characters, also the recessive ones with their peculiarities fully developed, and this occurs in the definitely expressed average proportion of 3:1, so that among each 4 plants of this generation 3 display the dominant character and one the recessive. [1]
Thus spoke ZaraMendel. He furthermore added "Transitional forms were not observed in any experiment." [1] Boom: blending inheritance you are no more!
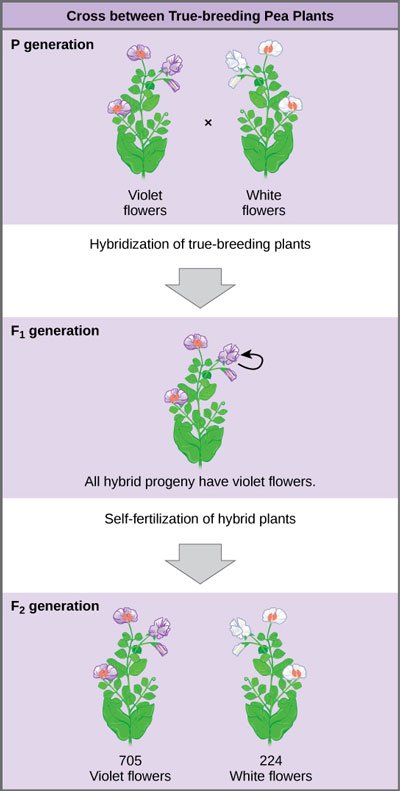
It's either violet or white: no blending!
Source: OpenStax, Principles of Biology
But notice the wording he uses in the first instance, where he talks about the ratios: "definitely expressed average proportion of 3:1". Yup, definitely average! As a philosopher I'm trained to pay attention to these things.
And then to investigate them: What does "definitely average" mean?
Well, I crunched the numbers, and apparently what it means is that the 3 to 1 ratio was absolutely nowhere to be found in his experiments. Nowhere. Except, if you average all the numbers. In which case, lo and behold, the ratio is still not 3 to 1! In fact, even if Mendel counted another billion plants, and all were in fact exactly of a 3 to 1 ratio, still it would never be a perfect 3 to 1 ratio unless every member of the statistic exhibited that ratio from the get-go, or exactly countered the deviance of another member. All you need is one stray and you'll always tend toward 3:1, but you'll never quite get there.
Mr. Mendel, Monk signor, the 3:1 ratio you gave us is practically the only ratio we don't see on that list. What gives?
Source: OpenStax, Principles of Biology, modified
I find it interesting, Platonically speaking — meaning the Ideas and Forms theory Plato came up with, that he said represents the way our human minds work — that Mendel jumped to an abstraction that wasn't completely warranted by the actual data. A computer, that does not have that kind of creative disposition, would simply give the real number: 2.96:1. Or 3.01:1. Or something.
But Mendel, as a human, saw something that strictly speaking wasn't there. He saw behind the numbers. He felt that they tended toward 3:1, even though he nowhere saw that exact number.
I apologize for pressing the point, but I find it fascinating.
It's the same way we call the sky blue, even though its color changes all the time, and even the same patch of blue sky isn't the same-colored all over. And yet we abstract from the patches to some general nebulous blueness. Even when the sky is at best a dirty white, we still call it blue, just because it's daytime and it's usually blue during daytime. We don't even really look, we just appeal to our average model of what the sky should look like. And that's what Mendel did: he looked at the data, and he said "it should be 3:1".
At any rate, what matters is that it works! And more than a hundred years after Mendel, molecular biology will come along and explain to us exactly why it works. [8] But I can't help but wonder how AI computer scientists are going to be able to replicate such creative mathematical thinking in robots. (Or, maybe they already have?)
F2: The Second Filial Generation
The further down the generations we go, the more interesting it gets. Here, in the second generation, the recessive traits — the ones you'd think were gone, if you had ended your experiment with the first generation — make a reappearance!
Furthermore, when the recessive plants are selfed (self-polinated, since pea plants carry both male and female parts), they produce "constantly" similar offspring. Whereas when the dominant plants are bred, they show the old ratio of 3:1 (or thereabouts!)
F∞ : Generation infinity
Mendel of course did many more generations, as a proper scientist should. But I'm not going to take you through all of them. A pic with the first 5 will of a more intricate experiment will suffice.
Ooh! New notations! I like!
Source: OpenStax, Principles of Biology
What's interesting to note here, is Mendel just came up with the way of representing big A for the dominant allele and little a for the recessive allele, something even schoolchildren who are just learning biology know about. Mendel has, in essence, discovered alleles: the two different versions of a gene.
He went on to cross several different characters together, and counted. Always counting in a Platonic manner, of course:
The ratios 10:19:43:78 agree so closely with the ratios 10:20:40:80, or 1:2:4:8 that this last undoubtedly represents the true value. [1]
And, in counting, he discovered many other things, among which is what was later called Mendel's Second Law, that of Independent Assortment. Here it is in his own hard-to-decipher words:
It is demonstrated at the same time that the relation of each pair of different characters in hybrid union is independent of the other differences in the two original parental stocks. [1]
All this he wrote in italics. And rightly so.
Let's now really justify the title of this post.
7 Chromosomes of Good Luck

Goddess Fortuna!
Source: Wikimedia Commons contributors
What the Law of Independent Assortment is saying, is that the various characters that Mendel studied were inherited completely independently. No trait among the ones he studied had a propensity to cling to any other. "Among the ones he studied" being the key phrase here.
We now know why these traits inherit independently. Because they're on different chromosomes. Mendel had no way of knowing that. It just so happened that he studied 7 traits, and they were all on different chromosomes. He not only picked the right traits, but he picked the right number as well.
But what if Mendel had studied 8 traits instead of 7?
Well, you have no way of knowing how to answer that question.
Unless I tell you that peas only have 7 chromosomes.
Dun-dun-dun!
Yes. That means that if Mendel had studied 8 traits, inevitably 2 of them would not assort independently.
And then, maybe, it would be "goodbye Mendel's Second Law".
This is important, he only gave us 3 laws altogether. Without the second, maybe Mendel would be a third less famous. And, instead of calling him the father of modern genetics [3], we would have called him the "stepfather". Who knows!
I kid. But Mendel did have great luck, so much so that it's led some researchers to doubt the honesty of his work, one statistician going so far as to claim Mendel's results were "cooked" [9]. Famous researchers, among them Punnett (yes, the same one who gave us the Punnett square to facilitate Mendelian offspring calculations, making students' lives much easier) replicated Mendel's experiments, but not his results. [10]
You see, I wasn't harping on about 3 to 1 ratios for nothing!
The whole affair has led to the so-called "Mendelian Paradox", which is the difficulty of reconciling Mendel's suspiciously great luck with his exemplary moral character.
Curtain Close: From peas to peeps
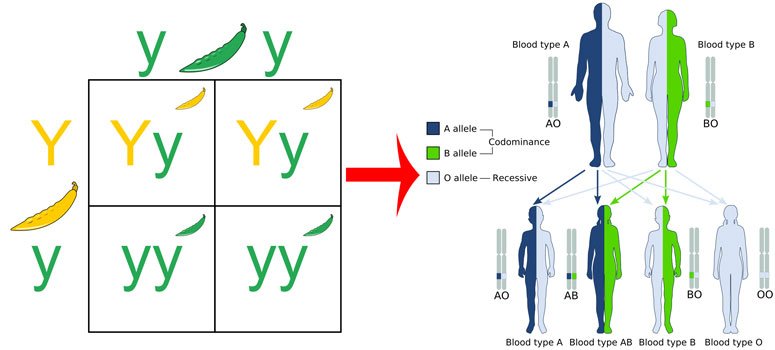
I almost made it through a whole post about Mendel without showing a Punnett square. Almost.
Source: Wikimedia Commons contributors1 & 2, modified
Cooked or not, one thing there's no doubt about is Mendel's contributions to the advancement of science, including human medicine. His discoveries, you see, weren't just about peas: they were about people.
His experiments gave us an answer to why certain traits, like certain diseases, "skip" a generation.
Science can now explain why certain alleles are recessive: because they code for proteins that are non-functional (e.g. white flower color), but if the other allele contains a functional protein (e.g. purple flower color), that's enough to "rescue" ("dominate") the non-functional allele (resulting in a purple, or "dominant", phenotype). [2] And that's as true for pea flower colors as it is for human diseases like sickle cell anemia.
The list goes on. Phenotype, genotype, allele, gene, homozygous, heterozygous, test cross, gametes — all terms that Mendel didn't use, but that he at least enabled, if not invented.
And it was all ignored during his lifetime. People either didn't get it, or the algebra was too much for them.
But Mendel's experiments, convoluted or not, are true paragons of science. When you learn about how science ought be conducted through textbooks — gather data, make observations, ask questions, formulate a hypothesis, design an experiment, set up controls, test your hypothesis — that's everything Mendel did to a T. He is a textbook scientist if there ever was one.
And he was meticulous to a fault. His work required "courage and persistence" [7] of a high caliber. I find it hard not to admire that. And even his Law of Independent Assortment, though we don't know if he would ever have formulated it had he studied more than 7 traits, still holds true to an extent:
With hindsight about the chromosomal location of genes, we now know that this “law” is true only in some cases. Most cases of independence are observed for genes on different chromosomes. Genes on the same chromosome generally do not assort independently, because they are held together on the chromosome. [2]
But for someone like Mendel, who despite his childhood poverty made such rich contributions to science, he could spare a law anyway!
References
Gregor Mendel, Experiments in Plant Hybridization (1865) http://www.mendelweb.org/Mendel.html
Griffiths AJF, Miller JH, Suzuki DT, et al. An Introduction to Genetic Analysis. 7th edition. New York: W. H. Freeman; 2000. Mendel’s experiments. Available from: https://www.ncbi.nlm.nih.gov/books/NBK22098/
Biography.com Editors, Gregor Mendel, Biography.com, Accessed December 10, 2017, https://www.biography.com/people/gregor-mendel-39282
Robert Bear, David Rintoul, Bruce Snyder, Martha Smith-Caldas, Christopher Herren, Eva Horne, Principles of Biology. OpenStax CNX. May 13, 2016 http://cnx.org/contents/db89c8f8-a27c-4685-ad2a-19d11a2a7e2e@24.18.
OpenStax, Biology. OpenStax CNX. May 13, 2015 http://cnx.org/contents/185cbf87-c72e-48f5-b51e-f14f21b5eabd@9.85.
Wikipedia contributors, "Theory of forms," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Theory_of_forms&oldid=813367218 (accessed December 9, 2017).
Miko, I. (2008) Gregor Mendel and the principles of inheritance. Nature Education 1(1):134 https://www.nature.com/scitable/topicpage/gregor-mendel-and-the-principles-of-inheritance-593
Mendel’s Genes: Toward a Full Molecular Characterization, James B. Reid and John J. Ross, Genetics September 1, 2011 vol. 189 no. 1 3-10; https://doi.org/10.1534/genetics.111.132118
Wikipedia contributors, "Gregor Mendel," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Gregor_Mendel&oldid=811572627 (accessed December 10, 2017).
Wikipedia contributors, "Genetic linkage," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Genetic_linkage&oldid=802601194 (accessed December 10, 2017).
Wikipedia contributors, "Punnett square," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Punnett_square&oldid=813061950 (accessed December 10, 2017).
Earlier Introduction to Biology episodes:
4: How Cells Use Logic To Do The Impossible
3 : Armchair Science — The Discovery of Proteins' Secondary Structure
2 : How Cell Membranes Form Spontaneously
1 : Eduard Buchner: The Man Who Killed Vitalism
steemSTEM is the go-to place for science on Steemit. Check it out at @steemstem or browse the #steemSTEM tag or chat live at steemit.chat
