
In Newtonian physics, both the position and velocity of a particle can be specified to an infinite level of precision.
Not so in quantum mechanics, where these are limited by Heisenberg’s uncertainty principle. A quantum particle simply does not have both a definite position and a definite momentum. In the same way, no process can occur at a definite time with a definite energy. This indeterminacy principle has many important consequences.

(Image of the evolution of gaussian wave function, a free particle in two-dimensional space, the color and intensity indicate its phase and amplitude.)
How is it that we can learn exactly where a quantum particle is, or where it is going, but not both at the same time?

Recall Laplace’s demon, an imaginary being who knows the present position and velocity of every particle in the universe. By applying Newton’s laws of motion, the demon should be able to perfectly predict the future. However, even a fairly simple system may be impossible to predict, because chaos makes even a deterministic system unpredictable. The same is true on the particle level, not because of chaos, but because of uncertainty, a fundamental aspect of quantum mechanics.
The uncertainty principle was discovered by Werner Heisenberg soon after quantum mechanics was invented.
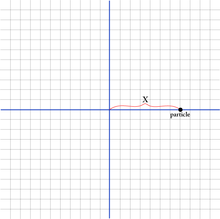
- Imagine a particle moving along a line motion in one dimension and call its position on the line
x. - The particle moves with a certain velocity
v. - Its momentum, p, is determined by its mass times its velocity:
mv = p.
In Newtonian physics, the particle always has a definite position in space and a definite momentum.
However, a quantum particle is described by probabilities; rather than definite values for x and p, there is a range.
We express this as ∆x, uncertainty in position, and ∆p, uncertainty in momentum. Their product is always greater than Planck’s constant: ∆x∆p > h. The more precisely we know x, the less precisely we can know p, and vice versa.
Planck’s constant, which determines the size of quantum effects, is extremely tiny:
6.63 × 10−34 kilograms per square meter per second
For an ordinary object say, a thrown baseball we could know its position and momentum to 15 or 16 decimal places. For minuscule particles like atoms, photons, and electrons, the numbers are so small that we can never hope for real accuracy. Then Heisenberg's Uncertainty Principle comes in....
End Part 4
PART 1, PART 2, PART 3, PART 4
Image Credits (in order):
https://i.ytimg.com/vi/ZpwZgOumTrs/maxresdefault.jpghttps://upload.wikimedia.org/wikipedia/commons/4/47/Uncertainty_principle.gifhttp://www.coasttocoastam.com/cimages/var/ezwebin_site/storage/images/coast-to-coast/repository/photos/pickover-images-laplace-s-demon/619858-1-eng-US/Pickover-Images-Laplace-s-Demon.jpghttps://upload.wikimedia.org/wikibooks/en/thumb/4/48/Particle.png/220px-Particle.pnghttps://upload.wikimedia.org/wikipedia/commons/thumb/6/65/Hydrogen_eigenstate_n5_l2_m1.png/330px-Hydrogen_eigenstate_n5_l2_m1.pnghttp://mental-ephemera.com/wp-content/uploads/2012/03/atom_baseball.jpg
