Critique of Devlin's article on Teaching Multiplication
The "5 times 3" Controversy never seems to abate. Keith Devlin, a professional mathematician has weighed in on the teaching of multiplication. He tells elementary school teachers not to teach multiplication as repeated addition. Although he qualifies statements by saying he is not experienced in teaching young children, many points that he mentioned in his article are moot.
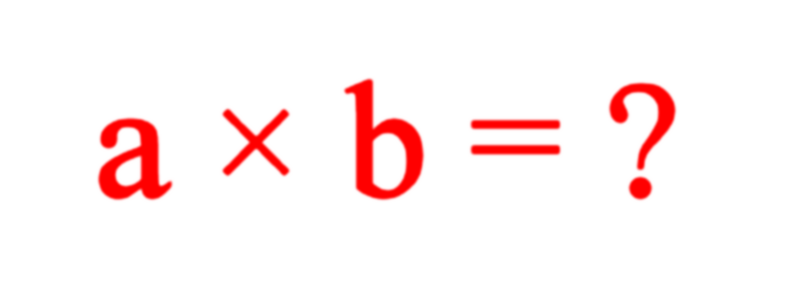
I want to first declare my position that "multiplication actually is repeated addition" is not a false belief. However, it is a limiting one if this is the only way multiplication is thought of as. I don't think it is wrong to teach multiplication as repeated addition (MIRA). Pupils have to start somewhere concrete. The real issue is the idea that "multiplication actually is just/only repeated addition". Many teachers have a poor or limited understanding of the maths themselves, without exposure to more advanced and/or alternative conceptions of "multiplication". Pupils taught under them risk being limited by their teachers' own understanding, if they do not themselves explore alternative learning resources (e.g. read beyond their school texts, or watch educational YouTube videos, or read my articles on Steemit ;-) ).
While pupils can start with MIRA, they should not stop at that. The multiplication concept can be extended in many ways. So one of the ways is stretching (or scaling). That is with non-whole number quantities.
When pupils learn negative numbers, you can have repeated addition (and even scaling) with mirror reflection, which Devlin did not mention.
Here are some more advanced / alternative conceptions of multiplication which are not alluded to:-
Multiplication can also mean rotation (not just scaling) in the context of complex numbers.
Then there is matrix multiplication, which is another animal.
Vectors have at least 3 types of multiplication: scaling with numbers, dot or scalar product and cross product.
After getting these off my chest, let us turn to Devlin's arguments. In his article, the statement 'We never ask the question "What is it?" nor do we seek to define it in terms of "more basic" functions. ' is suspect. His thesis that "multiplication simply cannot be defined as repeated addition" is not convincing. This seems to be argument by intimidation, a fallacious way of argumentation. I am sure professional logicians can break through "meta-schema outside the axiomatic framework". This is just multiplication, for goodness' sake. You just need some disjoint subsets and form their union, as I have illustrated this visually in my article here and and then you show a one-to-one correspondence with the Cartesian Product. If you want even more rigour, build up some induction machinery from Peano's axioms and do it from there. If you are worried about "well-definedness", then show that whatever objects are substituted on a one-to-one exchange with the product set involved in the multiplication and, and the aggregated set in the repeated addition (the union), you still get the same answer. This is excruciating detail, if you want to be pedantic. This is how Russell and Whitehead took about 300 pages to prove that 1+1=2. Yes, Gödel defeated Russell and Whitehead and all other schemes with his Incompleteness Theorems. But if you use Incompleteness Theorems as an excuse to cast doubt on the definition of multiplication, then a lot of our conventional mathematics is also game for nihilism. There are mathematicians who work at the foundations of mathematics. He should not presume to speak on behalf of all mathematicians. So his "we" does not include logicians and meta-mathematicians. If there is indeed a proof of the impossibility of defining multiplication by repeated addition, I would like to study the paper.
He then writes '(Sure, you can tell stories to extend the resulting RA notion to rationals, but it is "contrived", and the final jump to real numbers is problematic.' Oh yeah?
I find it very disrespectful of the great mathematicians like Cauchy, Dedekind, Bolanzano, Weistrass (to name but a few) to just gloss over the development of the concept of real numbers. Also, Kummer spent a great part of his life explaining how to rigorously extend from the integers to rational numbers and fields and more advanced concepts. These are the life work of many brilliant minds, spread out over hundreds of years to build mathematics of natural numbers, rational numbers, real numbers on a firm and rigourous foundation.
You might get away with identifying rational numbers, with lengths of lines, taking a geometrical approach. I guess that is a possible visual approach, akin to what the ancient Greek mathematicians like Euclid have done. But once you get into certain constructions requiring square roots (e.g. via Pythagoras' Theorem), you need to plug the "holes" caused by irrational numbers. And that is why we needed to develop real numbers, which is not a trivial feat for mathematics. So when Devlin presumed to speak for other mathematicians (dead and alive) about "multiplication", did he ask actually them or referred to their works?
Besides from the mathematical point of view, what is wrong with Devlin's proscription against teaching MIRA? Let us look at this from the pedagogical point of view. Piaget and Bruner have very well-founded theories from educational psychology that recommend teaching young children from simple concrete concepts and build on from there, according to their stage of development that they can handle. When you build a building, you start with the foundations. Yon do not build storey 3, then work your way down to the foundations, then progress to storey 4 and storey 5 and so on.
In my analogy, "multiplication as repeated addition" would be like the foundation. "Multiplication as scaling" is just storey 3. It is not even the highest level. "Multiplication as scaling plus reflection" would be like storey 4. "Multiplication as scaling plus reflection and rotation (as in complex numbers)", dot product, cross products, matrix multiplication would be like storey 5. And what is level 8? Maybe Product Topology or something of that sort. Level 9? Maybe Products in Category Theory? I am sure there are higher levels, but I am finding it hard to breathe in this rarefied atmosphere already.
So is it "a single wholistic concept" as he claims? But he also wrote " I say multiplication is complex and multi-faceted". Was he contradicting himself? This reminds me of the song "There Is a Mountain" by Donovan, which alludes to this passage from Zen Buddhism:
"Before I had studied Ch'an for thirty years, I saw mountains as mountains, and rivers as rivers. When I arrived at a more intimate knowledge, I came to the point where I saw that mountains are not mountains, and rivers are not rivers. But now that I have got its very substance I am at rest. For it's just that I see mountains once again as mountains, and rivers once again as rivers." (Qingyuan Weixin, as translated by D T Suzuki, Essays on Zen Buddhism.)
Our understanding of things is not static, but progresses through time. How we perceive things often reflects more of our level of understanding than the things themselves. This includes the concept of "multiplication". It starts with a simple version, like "repeated addition". We extend it and learn more advanced notions of the concept that seems different. You have a higher, expanded understanding. You see the differences (e.g. a×b = b×a is true for multiplication of numbers, but not for matrices, and a×b = -b×a vector cross products). But you also see common themes running through these concepts (something operated with another thing, and the result has some aspect that is proportional to both of those things in some way). Finally they unite to some sort of nirvana. Unfortunately, Devlin's favorite "nirvana" seems to be at level 3. This level is not the highest, nor the lowest. But he advocates this level as the starting point of learning multiplication. This is neither mathematically, nor pedagogically sound.
Argument from authority is a common form of argument which often leads to a logical fallacy. He says "I cannot for the life of me see why multiplication is not taught that way." The reason is because he is ignorant of educational psychology and mathematical history. Professors do not know everything. They just know more and more about a narrower and narrower field, until they know everything about nothing!
If the analogue of Ernst Haeckel's thesis that "ontogeny recapitulates phylogeny" even for the learning of mathematics, then the way a young child learns mathematics mimics the development of mathematics by mathematicians over history. Is there any exception to this? Can a young child spontaneously and effortlessly discover advanced concepts in mathematics without going through the more basic concepts? What about someone like Ramanujan, who discovered so many advanced mathematical formulas that stumped many other mathematicians? Well, even Ramanujan had to start with school maths and read books written by other people. Even if real numbers were naturally given from The Platonic Realm, the best of human beings need to build their concepts from the basic ones to the more advanced ones, and looking back to integrate their understandings. What more of lesser mortals, especially when they are of a young tender age?
