In yesterday's article, I was talking about finding the Highest Common Factor (HCF) a.k.a. Greatest Common Divisor (GCD) and the Lowest Common Multiple (LCM) using a calculator. Actually you don't need to use a calculator. If you can put the smaller number over the bigger number reduce the fraction to the lowest terms, you may just as well find the HCF and the LCM. It is preferable, but not compulsory to have the smaller number as the numerator.
What happens if you have more than 2 numbers? You just tackle the numbers two at a time. I issued challenge in the article and that is to find the HCF and the LCM of four numbers, namely 84, 210, 56 and 140. Here is my solution illustrated by a Hasse Diagram.
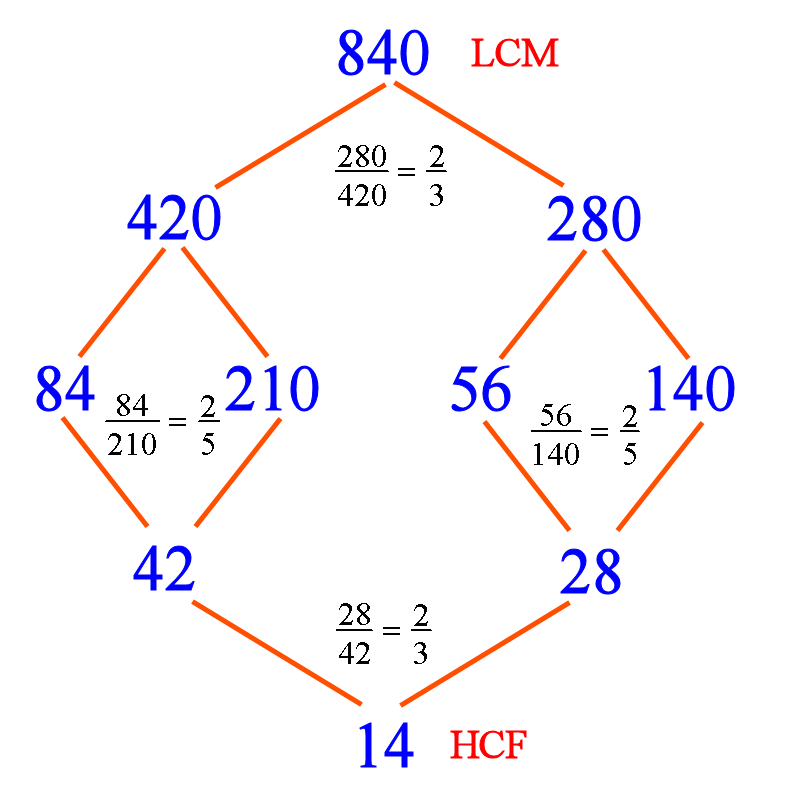
In a Hasse Diagram for factors and multiples, you connect a number and its factor with a line segment, with the factor appearing at a lower level. For example, 42 | 84 (42 is a divisor/factor of 84, or 84 is a multiple of 42). So you can see that if b is a multiple of a (i.e. a is a factor of b), then b (the multiple) is at a higher level. The “is a factor of” relation is transitive in that if a | b and b | c then a | c. For example, 14 | 28 and 28 | 56 and thus 14 | 56.
So how did I build this (simplified) Hasse diagram? I started by writing the four given numbers in the middle. I anaylse the four numbers in pairs: 84 with 210 and 56 with 140.
From , I get their LCM = 84 × 5 = 420 and their HCF = 84 ÷ 2 = 42,
From , I get their LCM = 56 × 5 = 280 and their HCF = 56 ÷ 2 = 28,
Working my way up with the common multiples, I now compare 420 and 280.
From , I get their LCM = 420 × 2 = 840 and this is the LCM of the given four numbers,
Working my way up with the common factors, I now compare 42 and 28.
From , I get their HCF = 28 ÷ 2 = 17 and this is the HCF of the given four numbers,
Although you do not really need a Hasse Diagram to solve this challenge, it clearly shows the inter-relationships between the factors and multiples, and it also makes my divide-and-conquer strategy very apparent. “Divide-and-conquer”, or breaking down a huge problem into smaller problems is one of the many useful problem-solving heuristics.
There are many interesting patterns and relationships in these diagrams. Let us start with a pair of numbers like 12 and 30.
From , I get their LCM = 12 × 5 = 30 × 2 = 60 and their HCF = 12 ÷ 2 = 30 ÷ 5 = 6.
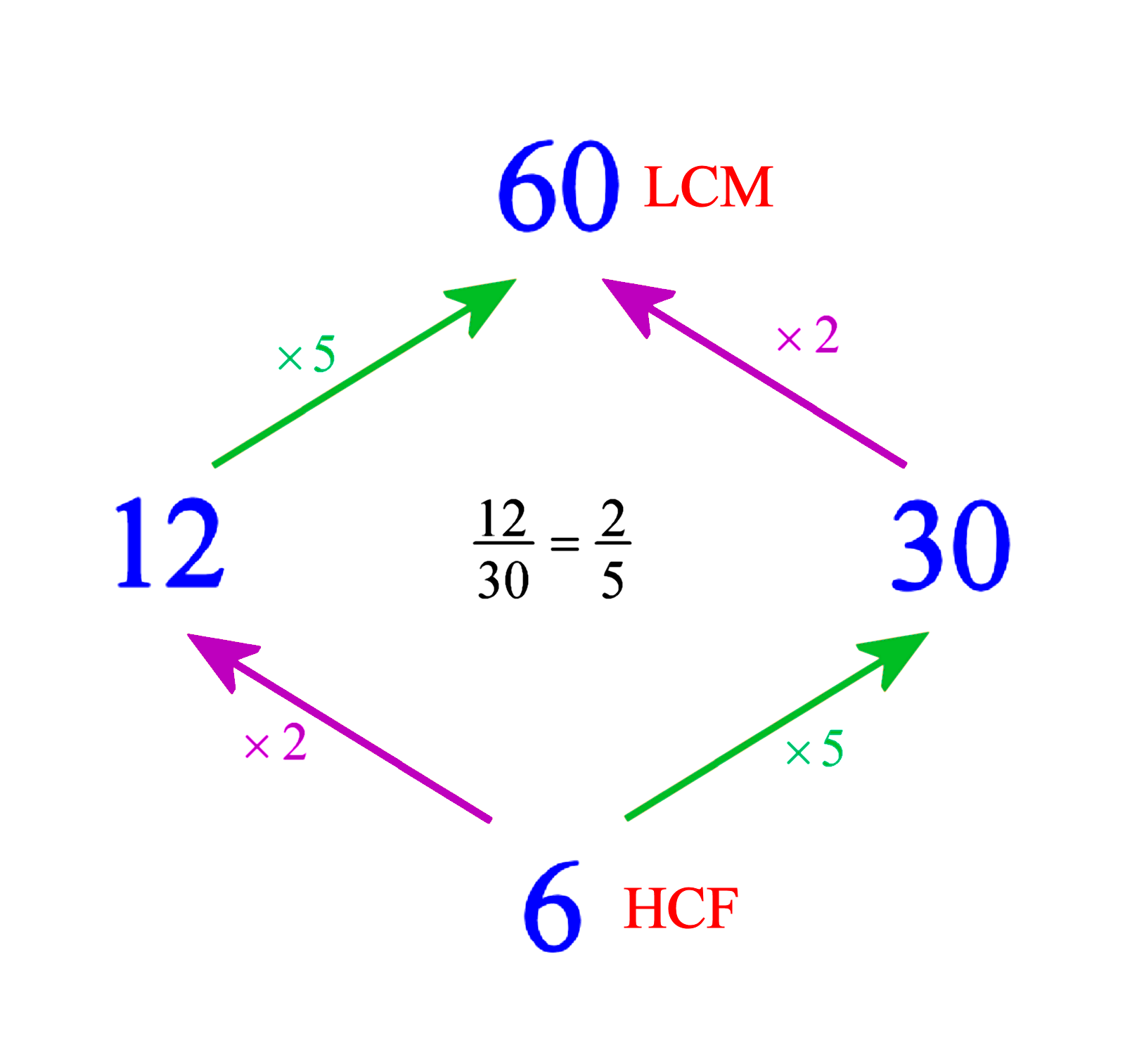
Do you notice that along the parallel sides of this “parallelogram”, the relations are analogous? 6 × 2 = 12 just as 30 × 2 = 60. See that?
Also 6 × 5 = 30 just as 12 × 5 = 60. Rephrasing this in terms of division, we can say that and
, One more thing:-
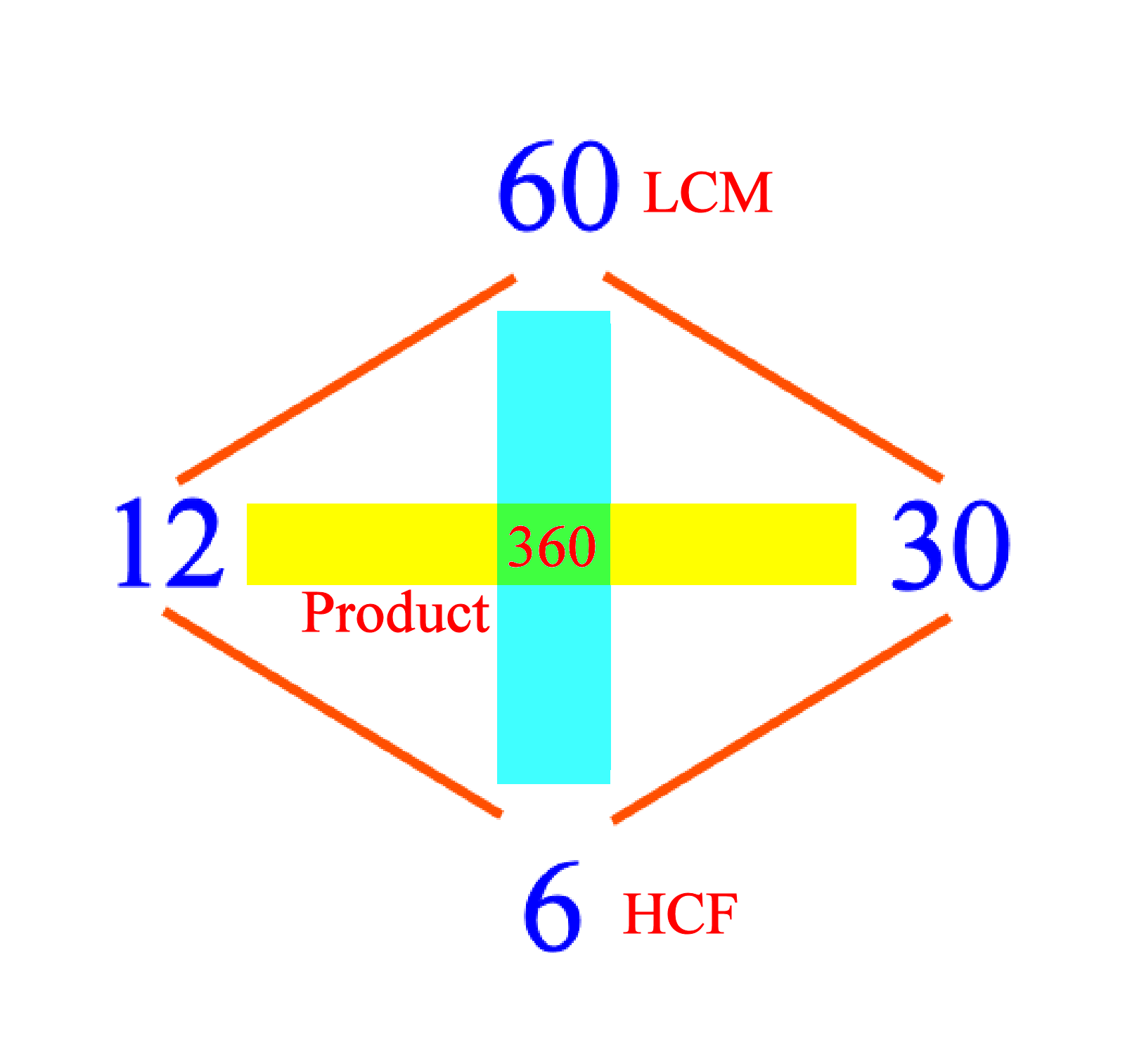
What happens when you multiply the numbers on opposite corners of the “parallelogram”? Do you notice anything? 12 × 30 = 360 and HCF × LCM = 6 × 60 = 360. That’s right: the product of two positive whole numbers is the same as the product of their HCF (GCD) and their LCM. If you consider the factors of 6 the HCF, (namely 1, 2, 3 and 6) you can extend the Hasse diagram downwards. We have 1 | 2, 1 | 3, 2 | 6 and 3 | 6 and these form another “parallelogram” structure (highlighted in pink). Actually, 1, 2, 3 and 6 are in fact the family of common factors of the original numbers 12 and 30, with 6 as the “head of the family”.
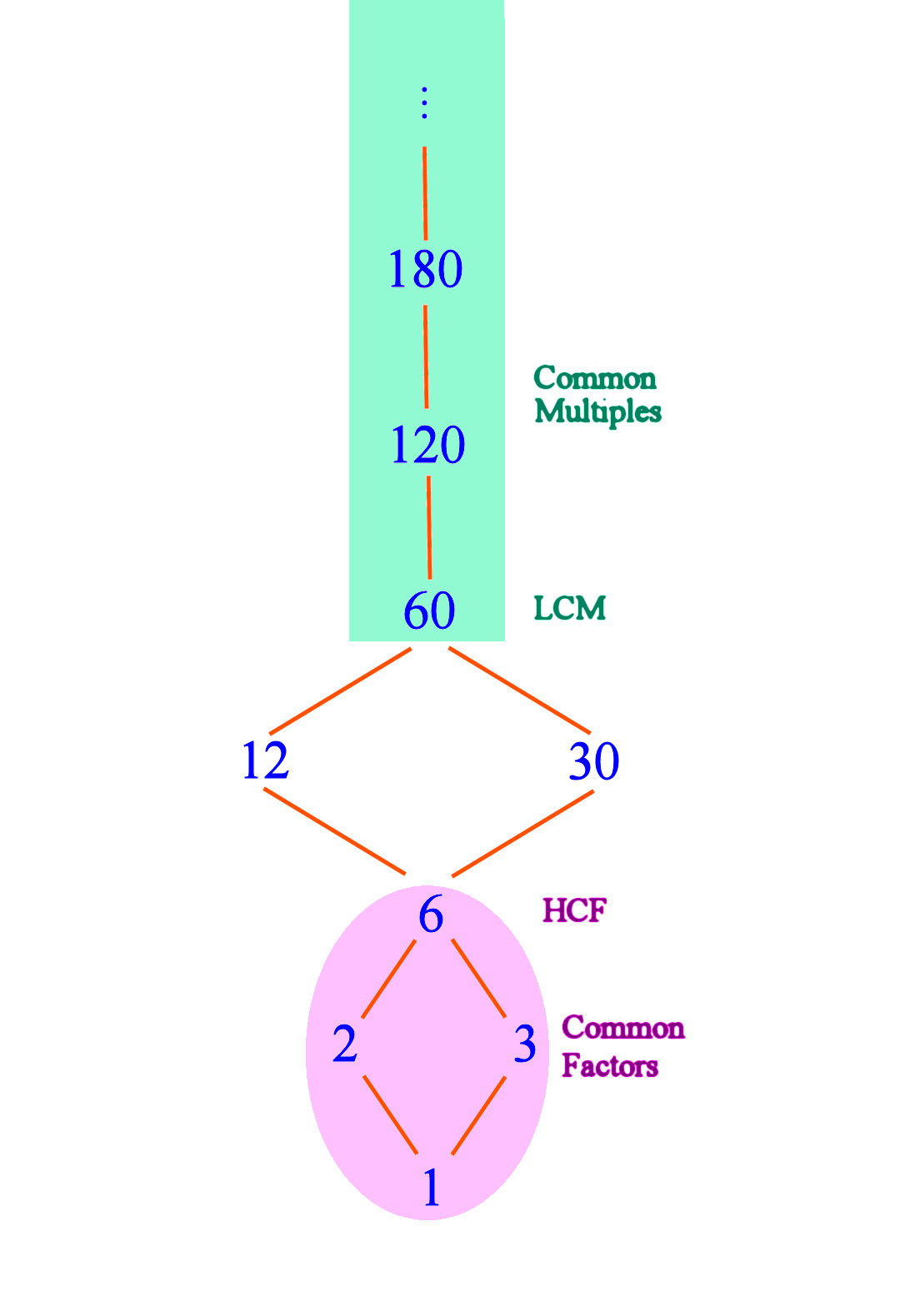
If you take the multiples of the LCM 60, you can extend the diagram upwards. The multiples of the LCM are 60, 120, 180, ... and so on ad infinitum, and they are exactly the common multiples of the original numbers 12 and 30. So these form another family (highlighted in turquoise i.e. that bluish-green colour). And 60 is the lowest number in the family of Common Multiples. No prizes for guessing why it is called the “Lowest” Common Multiple.
Cool, eh?
Try to draw a similar diagram for 140 and 60 on your own.
Try to do it yourself on a piece of paper.
Start by writing 140 and 60 in the middle row.
You may want to reduce 60/140 to its lowest terms.
What is the LCM? What is the HCF?
Can you extend the diagram upwards from the LCM?
Can you extend the diagram downwards from the HCF?
OK, you can compare with my diagram below.
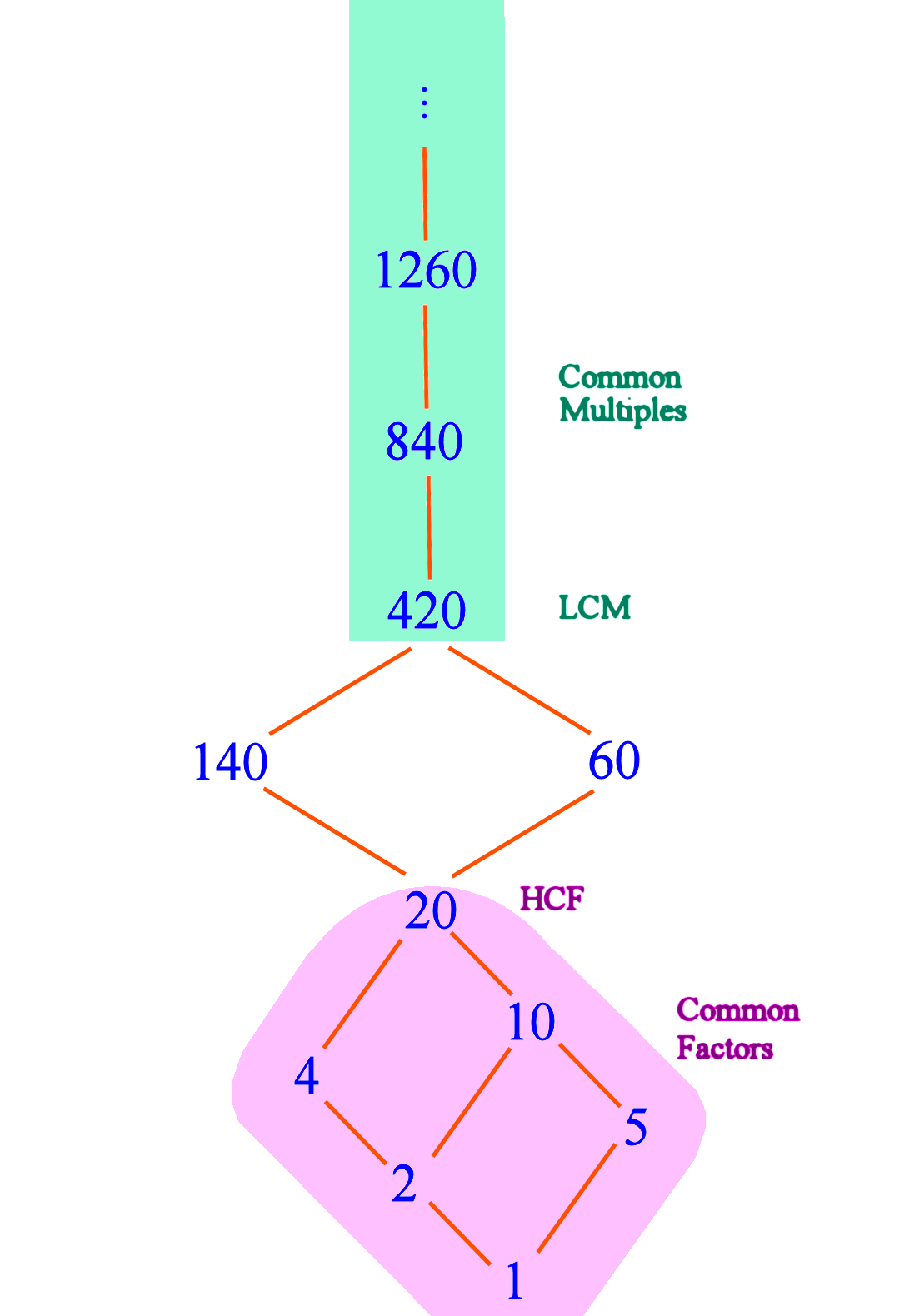
Now it turns out that the HCF 20 can be split into a few more ways. Compared to the previous example, there are more members in the family of common factors, and the common factors have a richer structure of inter-relationships among themselves.
I hope you have enjoyed my presentation and had fun with the Hasse diagrams.
Challenge for Today
Take the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10. From this set of numbers, link all the possible factor-and-multiple pairs in a Hasse Diagram. For example, you would link 2 and 4 with 2 at a lower level, and you would link 6 and 3 with 6 appearing higher. Where would prime numbers fit into the diagram? Where would the number 1 fit into the diagram? Where would the number 0 fit into the diagram?
Is it always true that whenever x is a factor of y, x must be smaller than y? Is/are there any exception(s) to this “rule”?
Have fun figuring this out and I’ll see you tomorrow!
Announcements
Please join my mathematics contest. SBD to be given away!
Please read my recent posts:
- Finding HCF and LCM via the Reduced Fraction
- importance of reflection after problem solving
- The Monk-Porridge Theorem
If you find my articles useful or interesting, please upvote and resteem them! See you tomorrow! Thanks to everybody for your support!!!
@tradersharpe
-- promoting sharp minds
