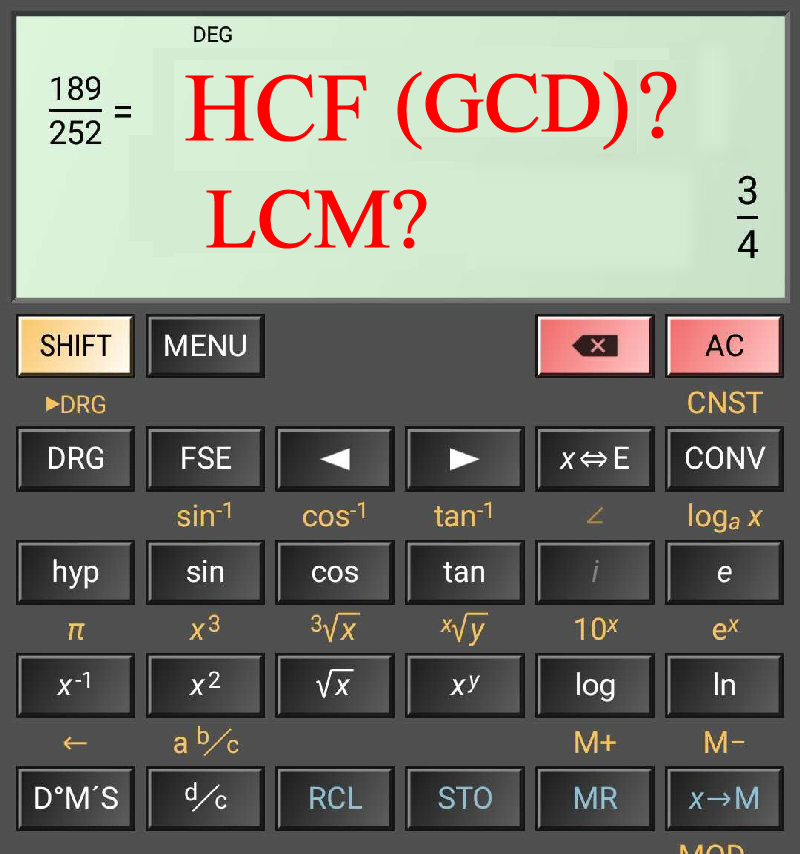
Today I shall share with you how to find the Highest Common Factor (HCF) a.k.a. Greatest Common divisor (GCD) in America, and the Lowest Common Multiple using the “fraction” feature that is available in most electronic calculators nowadays.
Look at the following fraction.
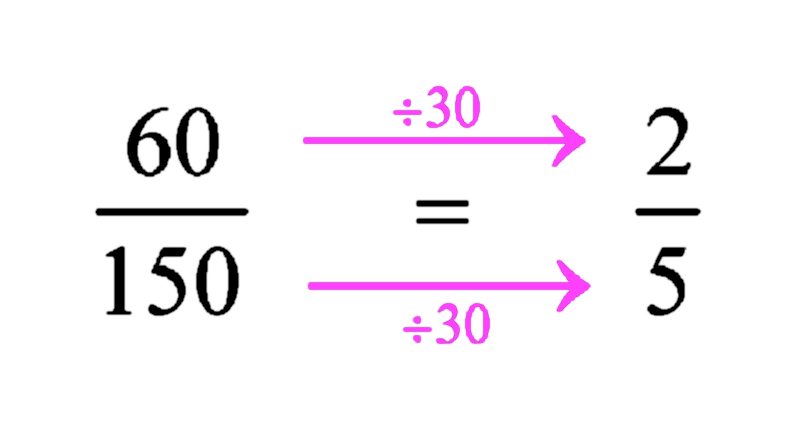
The fraction 60/150 is reduced to its lowest terms as 2/5. This is achieved by dividing both the numerator and the denominator by 30. Note that we must have divided by the Highest Common Factor (or Greatest Common Divisor) of 60 and 150. This is because in the lowest terms, all the common factors would have been cancelled out! If there is some common factor more to cancel, then it would not be in its lowest terms, or the “highest common factor” was not really the highest. Either way, this would not be possible. For the sharp reader, this is a “Reductio ad absurdum” argument. Any fraction must have been divided by the HCF (or GCD) of the numerator and denominator to get to the lowest terms. In our example, the HCF of 60 and 150 is 30. So if you key in the fraction 60 / 150 (using the fraction button, not the ÷ button) and it gets simplified to 2/5, you just take 60 ÷ 2 or 150 ÷ 5 to get the HCF viz. 30.
Now, what if you want the Lowest Common Multiple (LCM)? One of the interesting facts about numbers is that if you have two positive integers a and b, then the product of their HCF and LCM is exactly the same as their product!
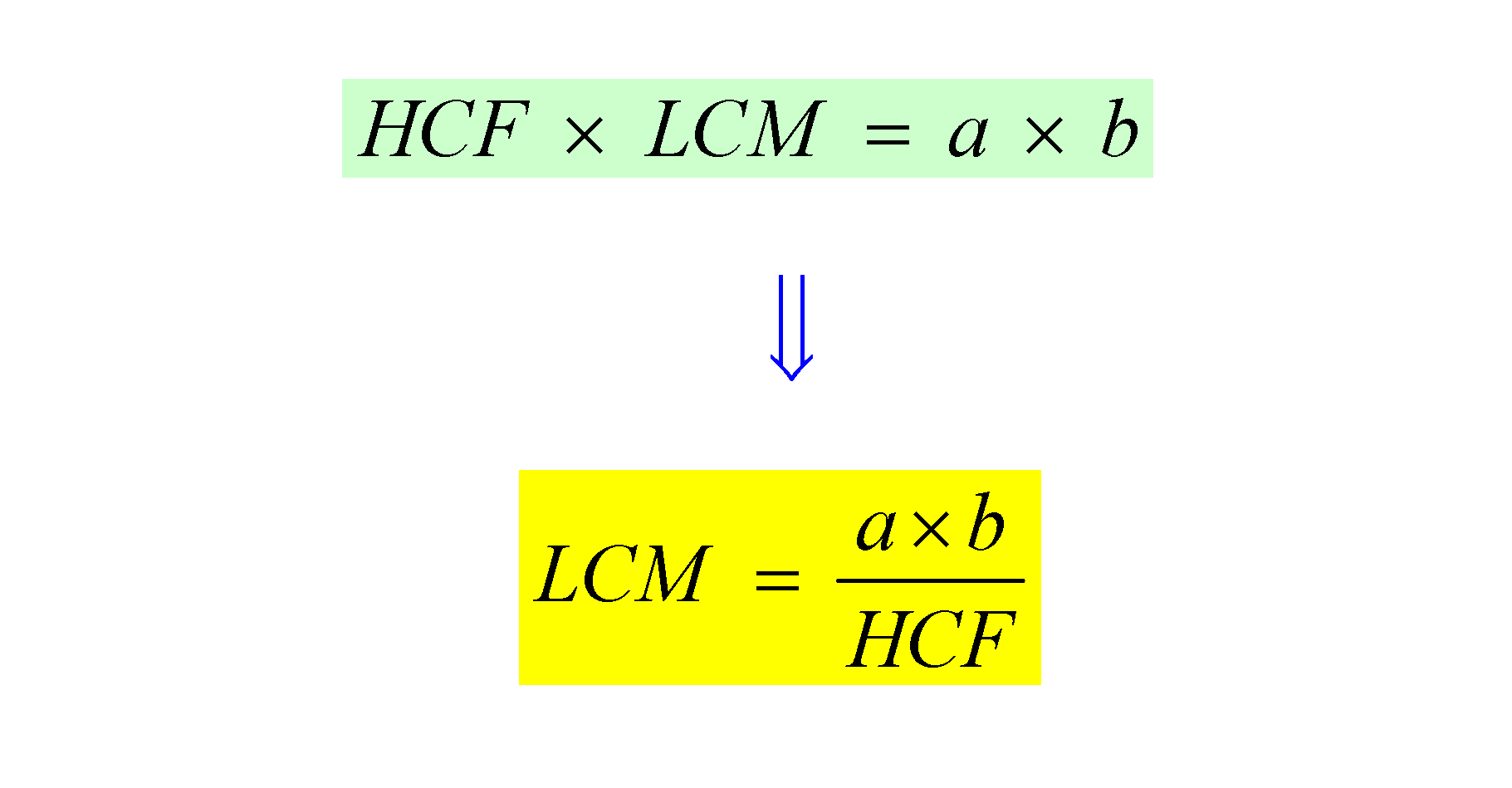
Using this fact, we can deduce that the LCM is equal to the product of the two numbers divided by their HCF. So the LCM of 60 and 150 is =
=
= 300. But let us look at the fraction and its lowest terms again.
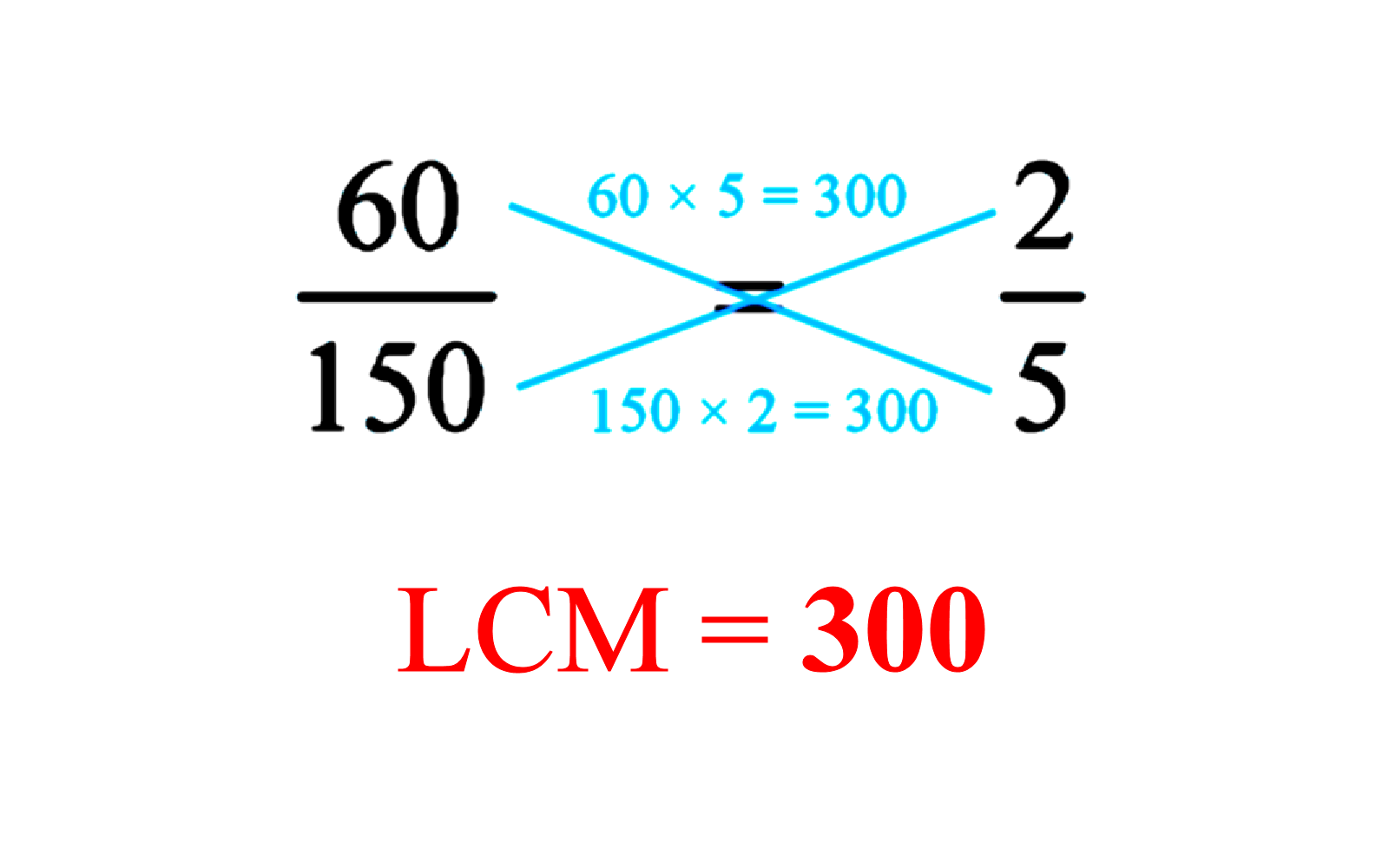
Do you notice something? If you multiply the numbers diagonally i.e. 60 × 5 or 150 × 2, both products will also give the LCM of 300. This gives another useful short-cut!
OK, let us apply our theory with another set of numbers. This time, we use 189 and 252. Find their HCF and LCM. The calculator will give you something like this:-
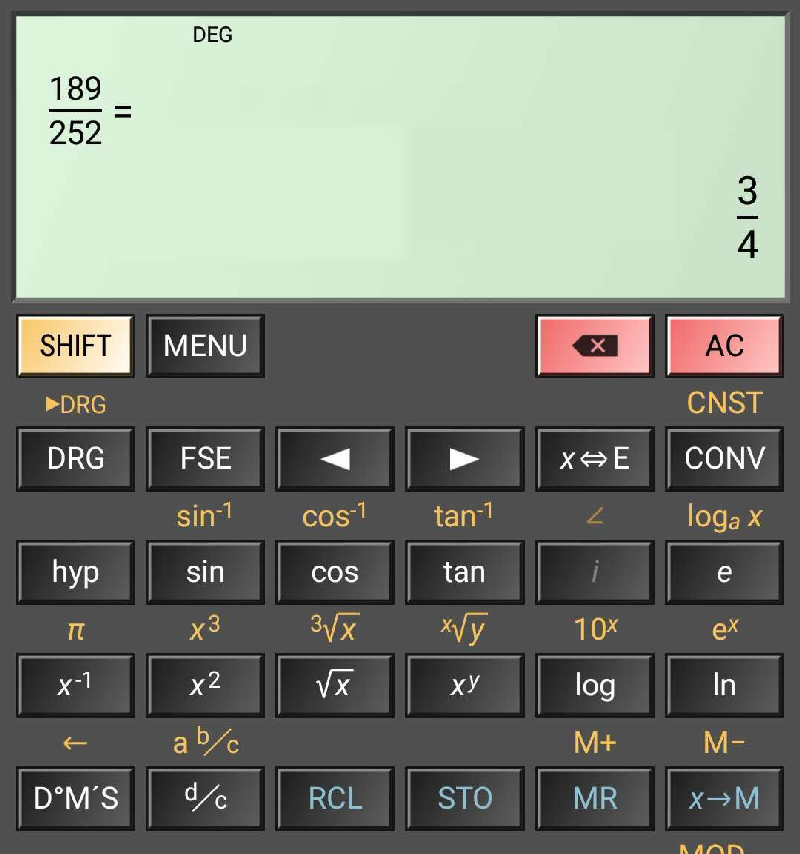
Now, HCF = 189 ÷ 3 = 63 or you can do 252 ÷ 4 = 63. To get the LCM, you can take 189 × 4 = 756. You can also take 252 × 3 and you get the same result. [In case you were wondering, I am using the “HiPER Calc” app for this example. You can use any calculator (or mobile app / emulator) that as the fraction calculation feature.]
I must warn you that the above theory and calculator tricks work only for two numbers. So what happens if you have 3 numbers? Then we tackle them two at a time. So let us say you want the HCF and the LCM of 44, 66 and 110.
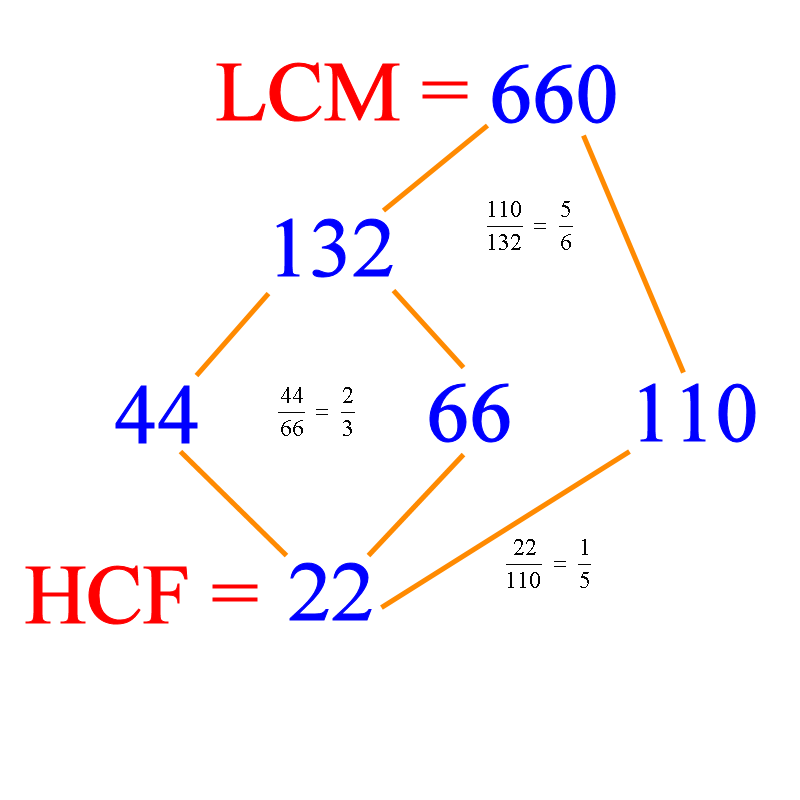
We can write 44, 66 and 110 in the middle of a piece of paper. From the calculator, you can get . So LCM(44,66) = 44×3 = 132. Write 132 on above 44 and 66 somewhere in between and join with line-segments. We also have HCF(44,66) = 44 ÷ 2 = 22. This is the HCF (or GCD) and we write this below and somewhere between 44 and 66. Join this to 44 and 66 with line-segments. Next we do the LCM of 132 and 110. From the calculator, we get
, so LCM = 110 × 6 = 660. This is also the LCM of the three numbers.
For the HCF, let us work our way down. We have already got HCF(44,66) = 22. Now, . This shows that HCF(22,110) = 22 ÷ 1 = 22. This is also the HCF of the three numbers.
In the diagram above, whenever a number is a factor of another number, we write the factor at a lower level and join the numbers with lines. This sort of diagram is called a Hasse diagram, and it really saves you from the hassle of navigating a mess of relationship between factors and multiples. So you can see, for example, that 22 | 44 (22 is a divisor or factor of 44 i.e. 44 is a multiple of 22). Other relations are: 66 | 132 and 110 | 660. What other relations can you see in the Hasse diagram? Note that the “is a factor of” relation is transitive i.e. if a|b and b|c, then a|c. For example, 22 | 66 and 66 | 132, so we know that 22 | 132. Observe that since 132 | 660, we also see that 22 | 660.
What if there are four numbers?
Challenge for Today
Find the HCF (GCD) and the LCM of 84, 210, 56 and 140.
We will discuss this tomorrow, and we will also talk more about Hasse diagrams for factors and multiples.
Announcements
Please join my mathematics contest. SBD to be given away!
Please read my recent posts:
If you find my articles useful or interesting, please upvote and resteem them!
@tradersharpe
-- promoting sharp minds
