
Just like Facebook relationships, roots can get "complicated". No, I am not talking about roots of plants or trees. I am talking about things like ,
,
and
. These are expressions involving square roots or cube roots. There can be other types of roots as well.
Such expressions are called "surds". If you think they are absurd, you are right! That is because most of these expressions are irrational numbers. Unless the root involved is also a whole number, the decimal expansion of the root would go on forever without any repeating cycles and we would not be able to express them as fractions. By the way, the words "surd" and "absurd" both come from the same Latin root (no pun intended).
How simplify these expressions? If you use a non-CAS calculator, the decimal expansions will terminate and the answers are actually not exact. They are approximated but not simplified if you use a calculator or software that can only give decimal digits. So how do we simplify them? Let us get to the root of the matter (no pun intended again).
Square Roots
For square roots, we try to first factor out square numbers or perfect squares. What are perfect squares? These are numbers that are square of some whole number. For example,
1 = 1² = 1 × 1
4 = 2² = 2 × 2
9 = 3² = 3 × 3
16 = 4² = 4 × 4
... etc
We know that when we take the square roots of numbers like 1, 4, 9, 16, 25, 36, 49, ... etc we will always get some nice whole number. This is how we simplify the square root of 48:-
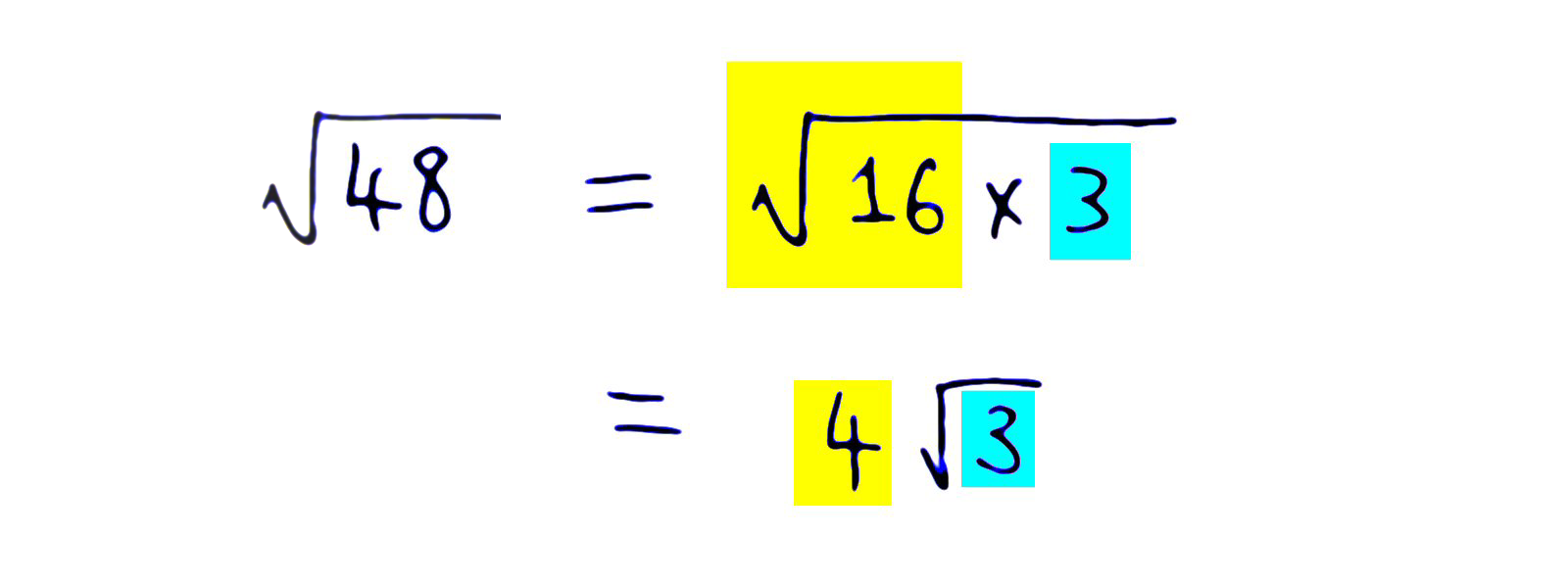
Factorise 48 as 16 times 3. The square root of 16 is 4, which is nice. The square root of 3 cannot be simplified. So we leave our answer as .
In mathematics, we often prefer the square root not to appear in the denominator. How do we get rid of the square root at the bottom? We multiply it by another square root on the denominator as well as on the numerator, like this:-
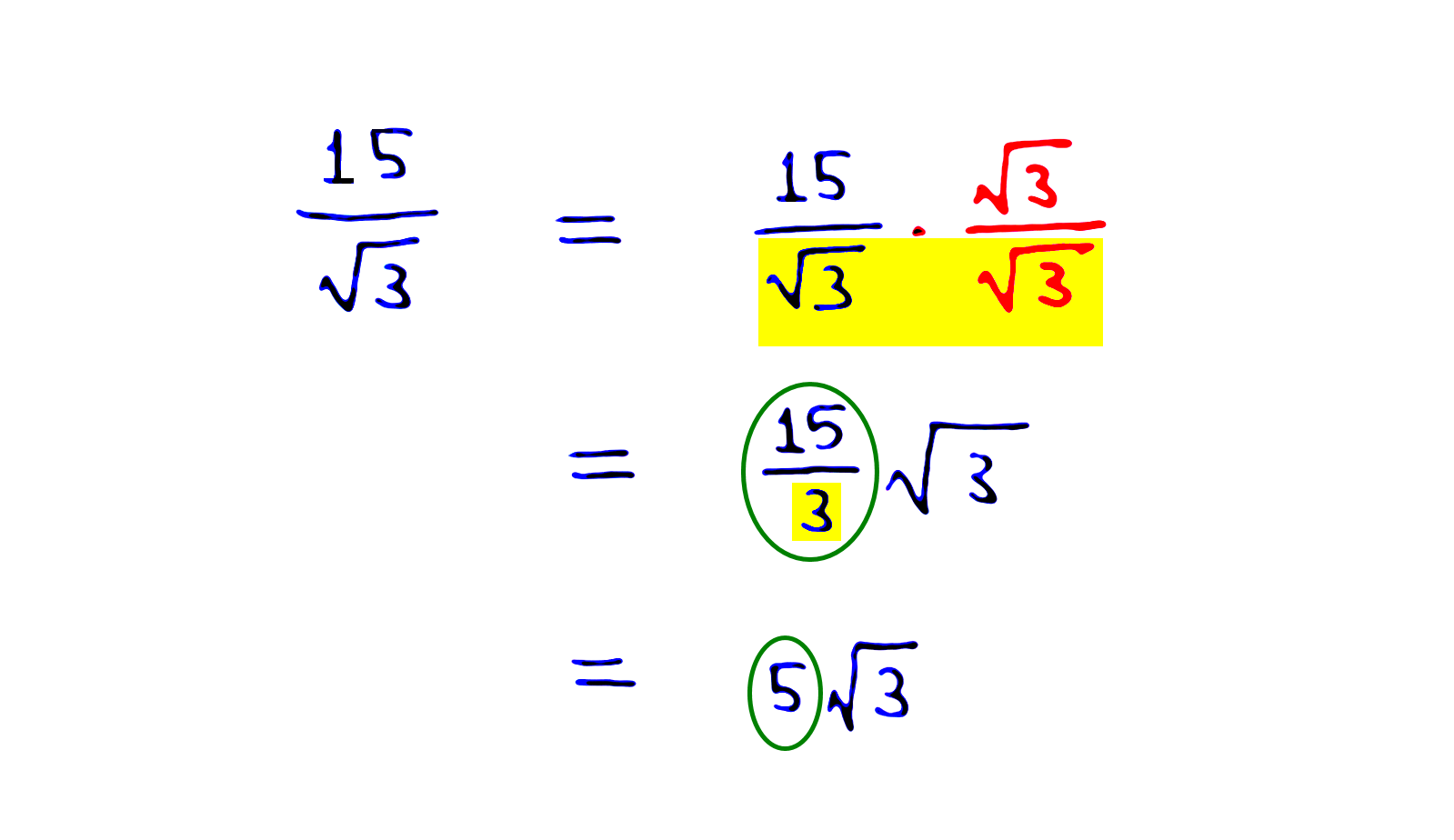
The square root of 3 multiplied by the square root of 3 is 3. Why? Because this is precisely what a square root means! By definition, the (principal) square root of a non-negative real number n is the non-negative number that, when multiplied by itself gives n. After the square roots merge to become 3, we can cancel 15 with 3 to give 5. The last line gives the final simplified answer.
Here is a more challenging example:-
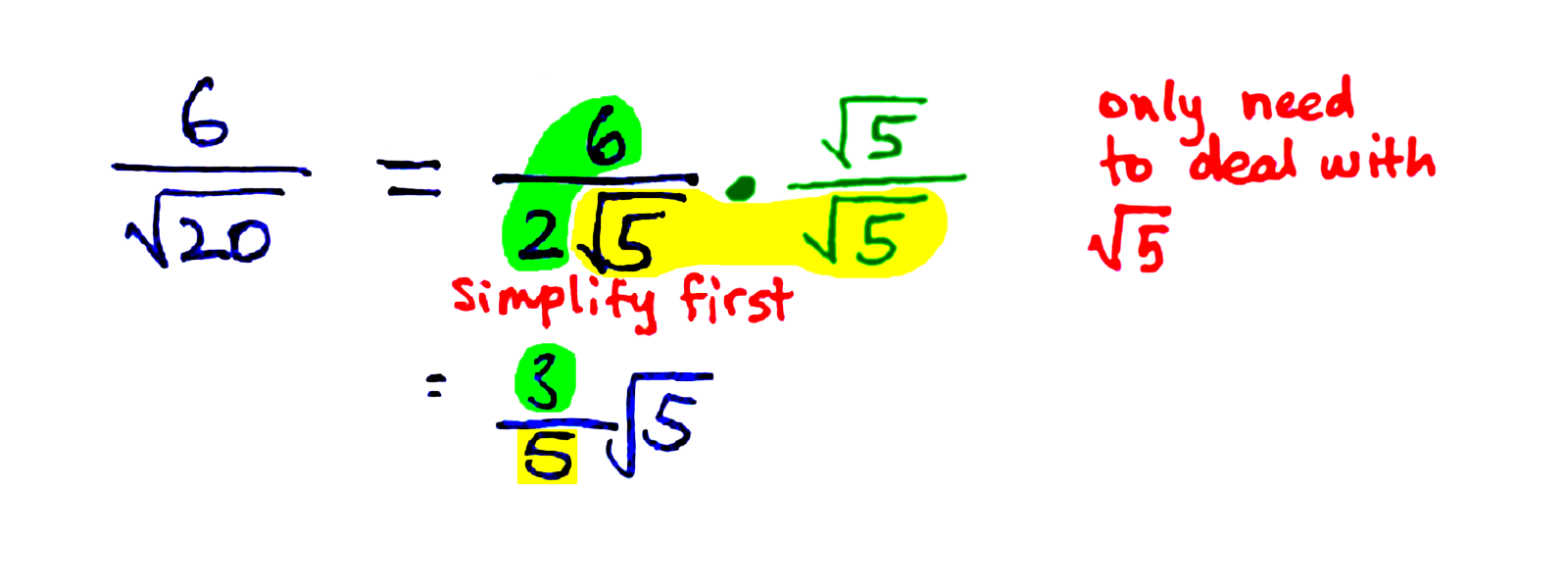
First, we should simplify the square root of 20. Note that =
=
. So we get a square root 5 at the bottom. To clear that away, we multiply the denominator and the numerator by square root 5. 6 cancels with 2 to give 3, while the two square roots of 5 merge to give 5. No further cancellation is possible and we have our answer
, which is the same as
.
Cube Roots
For cube roots, we follow a similar strategy. Take note of the perfect cubes
1 = 1³ = 1 × 1 × 1
8 = 2³ = 2 × 2 × 2
27 = 3³ = 3 × 3 × 3
64 = 4³ = 4 × 4 × 4
...
etc.
We simplify the cube root by factoring out any and all perfect cubes possible first. For example =
=
.
Computer Algebra Systems
For your information, calculators like Texas Instrument TI-89 have Computer Algebra Systems (CAS) in them, and are able to handle surd expressions symbolically. Below is a screen-shot from an emulator on my mobile phone.

I use an emulator on my mobile phone, so that I don't need to carry the actual real physical calculator when travelling around. Unfortunately students are not allowed to use such calculators or emulators in most schools and universities.
Wolfram Alpha is web-accessible and behind it is a powerful CAS called Mathematica. Even if students cannot use it for examinations, they can use it for learning. For example, you may set a question like "Simplify " for yourself and/or your classmates, try to do it yourself / yourselves, and see whether you get the correct answer.
Have fun exploring!
Image Credit
The first picture was derived from Pixabay. There rest of the images are all my own work.
Announcements
You might also want to read my recent articles:
"Singapore Math": The Ribbons Problem from PSLE 2017
How to plot vertical lines
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Cheers!!!
@tradersharpe
-- promoting sharp minds
