
Image Credit: Derived from CC0 image @ Dreamstime
This is not the first time that a mathematics problem from Singapore's high-stakes Primary School Leaving Examination (PSLE) has made the headlines and discussed all over. The question goes something like this:-

A few parents thought that this question was unfairly tricky.
For those of you who are still using imperial units, 1 metre is 3.28084 feet, or 39.3701 inches, and there are 100 cm (centimetres) in 1 metre. If the examination candidate forgot to convert the 110 cm into 1.1 m (metres), s/he is going to get this wrong. This is the first booby trap.
If you think: the total length needed is 200 × 1.1 m, so we just divide that by 25 m to get 8.8, so the answer is 8. Wrong! Gotcha!
Oops! Shoulda rounded it up. OK, er ... 9. Wrong also!
Why? Because each 25 m roll of ribbons does not contain a whole number of 1.1-metre lengths. There will be some left-overs and the problem does not mention the use of Scotch tape or anything like that to tape up the left-over bits.
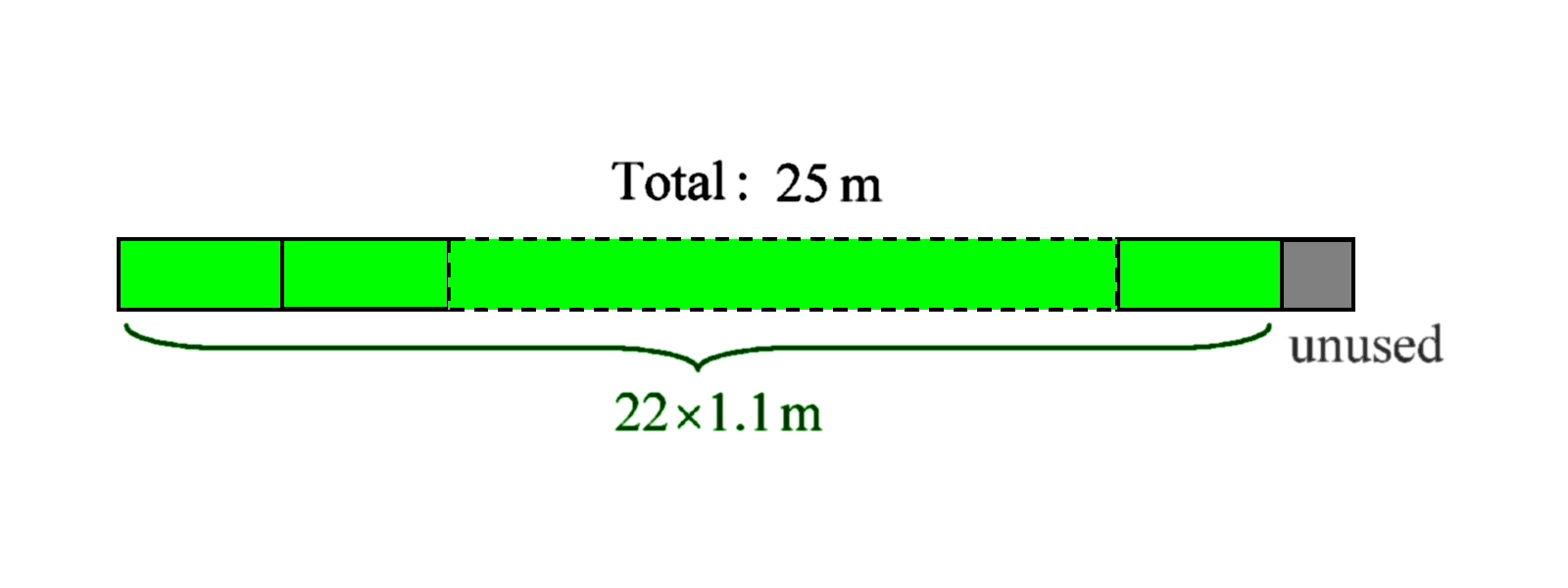
OK, let us try again. 25 ÷ 1.1 = 22.7, so we can get 22 full lengths of the ribbons. We are rounding down. If you rounded up to 23, "Gotcha!" again!
So each 25 m roll provides 22 ribbons. 200 ÷ 22 = 9.09, so we round up to 10, which is the correct answer. If you rounded down, you would only have 9 × 22 = 198 lengths of ribbons, which would not be enough. They never stop trying to get you even at the last step.
As you can see, the pupil has to be very careful and meticulous to walk through a minefield to get to the correct answer of 10. This question would trip up even adults, including the parents. Did you get it correct yourself?
Just to make sure that 10 is the correct answer, a team of people actually went out and solved it by the hardest way possible , and one of our professional vlogger comedians "Mr Brown" or "Kim Huat" joined in the fray with his tongue-in-cheek remarks.
So is the question unfairly tricky? My guess is that the folks at the education ministry want people to carefully and deliberately apply mathematics in the context (e.g. rounding up or down as appropriate), instead of blindly using mathematics. I would support that. The 2008 financial crisis was partly because people blindly and uncritically applied the mathematics to their financial models.
Is the question authentic? Is it real world mathematics? There is much to be criticised regarding assessment (including modes of assessment and authenticity of the assessment) in the field of education. What one child considers authentic may not be so for another child. Of course, in the real world, people do make allowances, concessions/compromises and approximations. But if we take up the challenge and solve the the conditions as stated in the examination question, then the calculations with the appropriate rounding-offs is what someone like Jessie would have to make. I think within the constraints of a pen-and-paper examination this is about as authentic as we can get.
What do you think?
If you have a better, cheaper and/or more authentic method of assessing pupils en mass, I would like to hear from you. Please comment below.
Announcements
You might also want to read my recent posts:
How to plot vertical lines
Visual Division of Non-Unit Fractions
The Sharp Mathematics Contest #2 -- Winners
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Cheers!!!
@tradersharpe
-- promoting sharp minds
