Curtain open
Pick up any introductory biology textbook, and out of the handful or so defining properties of life that they list with little variation, there is one that seems to stand out particularly well: life's ability to create and maintain order. [1]

Life is highly ordered.
Source: Wikimedia Commons contributors, modified
The reason this quality stands out more than the rest, is because life's propensity to form order seemingly defies one of the cardinal laws of nature: the second law of thermodynamics, which states that the entropy of a system never decreases.
A more vernacular — and more terrifying — way some choose to state this law, is to say that disorder always increases, and the universe tends toward randomness, or "corruption". Check out this TED talk if you've been wanting to watch a horror flick but can't find any that has good IMDb ratings. (I highly recommend watching this talk. By the end of it you'll have become scientifically convinced that absolutely everything you do makes the universe worse off!)
Viewed in these terms, life is fundamentally antithetical and antagonistic to reality. In this post I'll zoom in on just one of the many ways in which life battles pernicious disorder, and is, however temporarily, able to gain the upper hand. Specifically, I'll talk about how cells use logic to make otherwise impossible chemical reactions move forward, in what is more formally called "reaction coupling", but which I just like to call "cells that know their Aristotle"!
A detour
But first, we need to know a bit about Gibbs free energy, to understand the kind of impossibility cells literally have to surmount.
In order for cells to provide us with the energy that will lead to the orderliness that we perceive every time we stand in front of the mirror (actually, I think one of my nostrils is bigger than the other; but I digress), each one of these cells needs to perform "millions of reactions every second" [1].
Some of these reactions are spontaneous, meaning they will happen on their own, without external energy input. This is expressed in Gibbs graphic formulae like so:
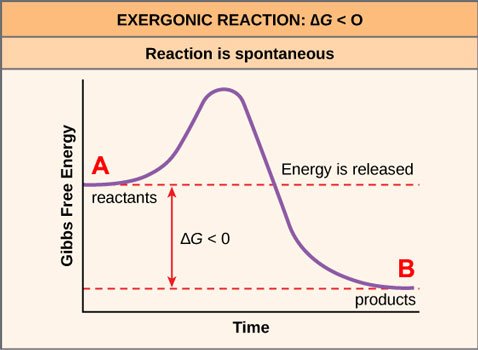
Source: OpenStax, Concepts of Biology, modified
I've labeled the product as B and the reactant as A. B is lower than A, which in Gibbs lingo means that B is more energetically favorable than A. (Here's a mnemonic device: it's easier to go downhill than uphill.) The reaction A to B, written as A→B, will therefore move forward spontaneously.
If you remember the second law of thermodynamics, you already know what this means: A→B is a move from order to disorder.
Yikes!
If you have the kind of inquisitive brain that I do, this still doesn't make sense to you: why is a move from order to disorder easier?

A highly ordered clothing store is one rife for disorder!
Source: Pixabay
To explain this using an everyday example, think of a clothing store that does not have employees to refold and replace the clothes that customers try on. Will that clothing store tend toward disorder, or toward order? Common sense says it will tend toward disorder. But why?
The reason is because there is only one way for order to be achieved — the one that the designers of the store have deemed ideal — and a great number of ways in which it can become disordered (especially if the customers bring their kids along). So, by the mere laws of probability, the store will become disordered — unless employees are hired to actively work to maintain order. Here's a way to graphically represent what the employees do:
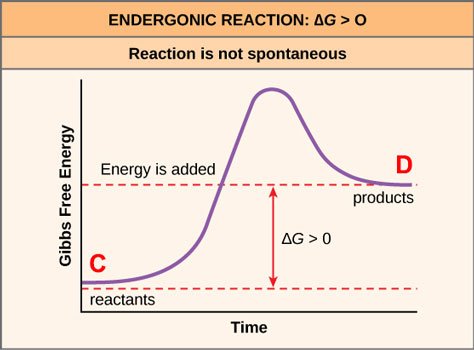
Source: OpenStax, Concepts of Biology, modified
So the reaction from disorder to order (C→D) in this case is unfavorable, and requires employees expending energy in order to drive it forward, and sometimes these employees must surmount significant psychological barriers in order to force themselves to keep up their work and/or not to lash out at the sheer thoughtlessness of some customers!
Again, I find it very useful to refer back to our second law of thermodynamics: after all, all these parochial examples are just specific instances of global laws.
So if we think of it in terms of the second law of thermodynamics, sometimes order and disorder are easy to grasp intuitively. For example, if you know that a catabolic process takes the food you consume and breaks it down into smaller particles, and an anabolic process takes those small particles and builds them back up into proteins your body can use, which process do you think will require more energy? In other words, which process represents the Gibbs graph that moves from order to disorder, and which process represents the Gibbs graph that moves from disorder to order? Hopefully your answer will match this image:
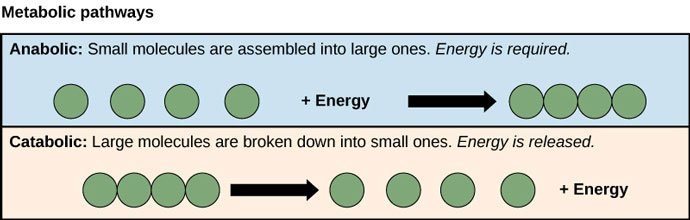
Source: OpenStax, Concepts of Biology
Even in catabolic processes, however, some work is often required. This is represented in the Gibbs graph as an activation barrier: it's the little "hill" or "bump" you see in the middle (we'll revisit it later). The reactant is quite happy being where it is, in its little organized state, but a spark is all it takes to move it forward (over the activation barrier). A wood won't spontaneously catch on fire, but once a spark has lit it, beware forest!
I like to liken the activation barrier to what in human psychology they call status quo bias or resistance to change. We always favor our default position, and have to be pushed over an "activation barrier" (in the form of a well-presented argument, for instance) to adopt a new one. It appears we are like cells in this too. Metaphorically speaking.
So what do cells do about activation barriers?
Enzymes

You're not having a déjà vu: this is the same graph as the first one.
Source: OpenStax, Concepts of Biology, modified
Going back to our spontaneous A→B reaction, what's interesting to note here, is that the graph tells us the reaction will take place, because the product (B) is in a lower (more "favorable") energy state than the reactant (A). However, it doesn't tell us how long the reaction will take. For all we know, it might take centuries for all the reactants to become products.
Now I don't know about you, but I don't have hundreds of years to wait, and neither do my cells, which, as mentioned above, have to perform millions of these reactions per second in order to keep me alive.
In order to make these reactions happen faster (in order to make the graph less of a bumpy ride and more of a slide), cells recruit enzymes, which are proteins whose job is to speed up, or catalyze, reactions. "Enzymes are among the most effective catalysts known, speeding up reactions by a factor of as much as 10^14" [1] Yes, that's a 10 followed by 14 zeroes!
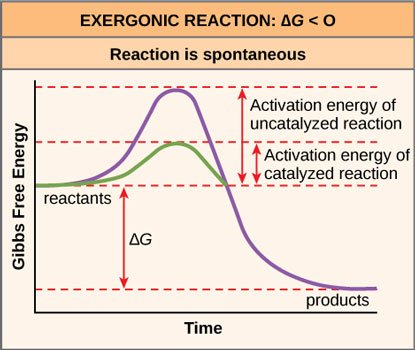
Source: OpenStax, Concepts of Biology
When cells do logic
But what happens when the product is higher than the reactant? Cradle as it may, the enzyme cannot turn an unfavorable reaction into a favorable one: all it can do is lower the activation barrier. What does a cell do then?
C to D (C→D), as you remember, is an unfavorable reaction. But A to B (A→B) is a favorable reaction. Let's say it's a very favorable one. What if the enzyme handles both these reactions, so that their product is a favorable one? In other words, what if there was an enzyme that took A+C and gave us B+D (A+C→B+D)? Now we've made an unfavorable reaction into a favorable one! It's not much unlike a businessman using his flourishing business to keep his failing (but promising) one afloat.
The mathematically trained cell often uses ATP (adenosine triphosphate) to make this happen. This is the reason ATP is considered the energy currency of the cell [11]. Whenever a cell wants to make something energetically unfavorable happen, it turns to ATP. The enzyme takes the ATP, removes a phosphate, turning it into an ADP (adenosine diphosphate).
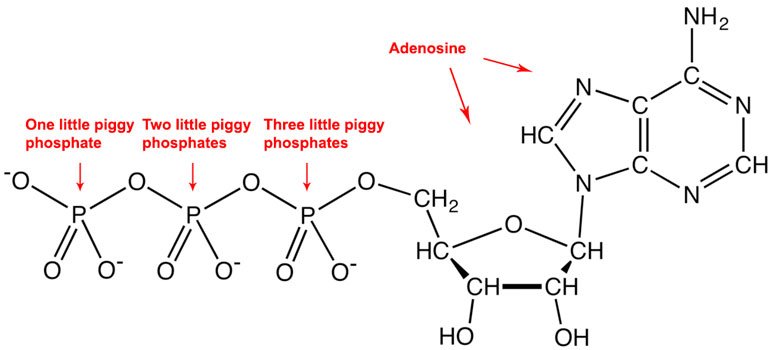
I made the counting from left to right, but if you're naming them for a test, then you had better go the Japanese way!
Source: Wikimedia Commons contributors, modified
If you've been paying attention, you don't need to know the details to understand why breaking apart a molecule ("creating disorder") releases energy. The ATP however is particularly reactive — chafing at the bit, so to speak, with those negatively charged (-) phosphates right next to each other, pushing each other away — which is why the cell uses ATP to get energy when it needs it, coupling it to unfavorable reactions in order to drive them forward. More than a hundred of these ATPs are in a typical cell at any moment, ready to "fire away", and in many cells this amount is used up and replaced every couple minutes [2].
Logic 2.0
There is something else that determines energetic favorability: it's not just absolute like the simplified model shown in the Gibbs graphs. The concentrations matter. If we've got a lot of Bs and very few As, the solutions will reach an equilibrium. Some of the Bs might even start going back to As, even if the reaction, absolutely speaking, favors the reverse.
To make this clearer, let's go back to the clothing store example for a minute. If the clothing store is ordered (A), then it is highly likely that any change will make it more disordered (B). If, however, the clothing store is highly disordered (many Bs), then the reaction could run backwards: a customer, no matter how thoughtless, might make a change that actually makes the store more ordered (B→A).

A highly disordered clothing store is itching for some order!
Source: Flickr
So what does the cell do in that case?
It takes a formal logic class, of course.
And after that, it knows what to do. Since the problem is too many Bs, turning Bs to something else, like Cs, will make As start turning to Bs again. It's a chain reaction! Or, rather, a chain suction! It's like sticking a straw at the bottom of the drinking glass instead of the top, and by sucking the lower liquids you're helping the top ones come down as well.
And there's no limit to the number of reactions I can do this to. It can be A→B→C→D→E→F and so on, I can pull forward a great number of reactions by just manipulating the last one.
When the reactions are linked together in long series like this, they are called pathways. They can get quite involved. More involved than the New York City Subway.
Yeah, I guess that's a good place to stop then!
Gladly we don't have subways where I'm from. We do have Subways though. Yummy!
Source: Wikimedia Commons contributors
Curtain close
Biology had invented mathematics and logic long before us. Well, strictly speaking, their workings can be described and understood in mathematical and logical language.
And that's how I like it. I like being able to understand the general, and derive the specific. There's just too many specifics to remember! But if you're able to really grasp the general — like the second law of thermodynamics, for instance — you can get a handle on any specifics life throws at you. Hopefully I've been successful in not weighing you down with the biochemical details, but helping you appreciate the principle of it, the mathematical logic of the thing.
And it can teach us a lot, this logic. Cells, you see, are very effective. For example, cells harvest nearly 50% of the energy that could potentially be derived from the oxidation of glucose and fatty acids; in comparison, a typical human-made car engine can turn no more than 20% of its fuel's potential energy into useful work [2]. I know, pretty lame! As aggregations of cells, we ought to do better than that!
References
Alberts B, Johnson A, Lewis J, et al. Molecular Biology of the Cell. 4th edition. New York: Garland Science; 2002. Catalysis and the Use of Energy by Cells. Available from: https://www.ncbi.nlm.nih.gov/books/NBK26838/
Alberts B, Johnson A, Lewis J, et al. Molecular Biology of the Cell. 4th edition. New York: Garland Science; 2002. How Cells Obtain Energy from Food. Available from: https://www.ncbi.nlm.nih.gov/books/NBK26882/
Wikipedia contributors, "Second law of thermodynamics," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Second_law_of_thermodynamics&oldid=812704510 (accessed November 29, 2017).
Wikipedia contributors, "Entropy," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Entropy&oldid=812587662 (accessed November 29, 2017).
Atkins, Peter. (2015, July 1). The second law, why worse can be better | Peter Atkins | TEDxOxBridge
OpenStax, Potential, Kinetic, Free, and Activation Energy. OpenStax CNX. Sep 30, 2015 http://cnx.org/contents/16b284a1-de63-4e08-910a-8baf1b94fc1e@7.
OpenStax, Energy and Metabolism. OpenStax CNX. Jun 1, 2013 http://cnx.org/contents/ed5df737-77ff-452c-b91e-a2c2dad59606@8.
Wikipedia contributors, "Status quo bias," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Status_quo_bias&oldid=810037779 (accessed November 30, 2017).
Furnham, Adrian. Resistance to Change. Psychology Today. https://www.psychologytoday.com/blog/sideways-view/201610/resistance-change
Wikipedia contributors, "Metabolic pathway," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Metabolic_pathway&oldid=811366067 (accessed November 30, 2017).
Wikipedia contributors, "Adenosine triphosphate," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Adenosine_triphosphate&oldid=811954010 (accessed November 30, 2017).
Earlier Introduction to Biology episodes:
3 : Armchair Science — The Discovery of Proteins' Secondary Structure
2 : How Cell Membranes Form Spontaneously
1 : Eduard Buchner: The Man Who Killed Vitalism
steemSTEM is the go-to place for science on Steemit. Check it out at @steemstem or browse the #steemSTEM tag or chat live at steemit.chat
