Drosophila melanogaster: the common fruit fly

_{Source: Wikimedia Commons contributors}

Introduction

Alfred Sturtevant (not pictured above) was a biology undergrad who pulled an all-nighter and solved one of the greatest mysteries in genetics, to the detriment of his homework.

I know, bad student.

If you're thinking, "no one spends a night and solves one of the greatest mysteries in genetics", then you're absolutely right, because here are Sturtevant's exact words:

I went home and spent most of the night (to the neglect of my undergraduate homework) in producing the first chromosome map. [1]

Most of the night, not the whole night.

Just as you said.

But why was the chromosome map so important, you ask?

Well, you're in luck, dear reader, because that just so happens to be the subject of this post. So hop on this fruit fly's back, and let it take you on a fascinating genetics adventure!

Crossing Flies

In case you didn't know what "crossing" means.

_{Source: Wikimedia Commons contributors, modified}

Not every story begins with sex.

But this one does.

It's a story about how two flies produced offspring whose phenotypes (traits) showed an unexpected ratio.

If you remember your high-school biology — and if, more specifically, you remember your Mendel and your Punnett squares — it won't be too hard for you to predict the offspring that will result from this cross: black-eyed male fly x white-eyed female fly. (The letter 'x' stands for 'cross'. Apparently, some internet sites prefer to write it as 'xxx', but let's keep this vanilla.)

Mendel's Law of Independent Assortment will come in handy here. The law states that traits are inherited completely randomly. So if you got an X number of traits (or phenotypes) and a Y number of offspring, the traits will be divided equally among the offspring, because that's what random means: equal. That's why, given only two possible outcomes, a series of coin tosses will give you an equal 50-50 chance of heads and tails.

So, presumably, the above fly cross will give us something like this:

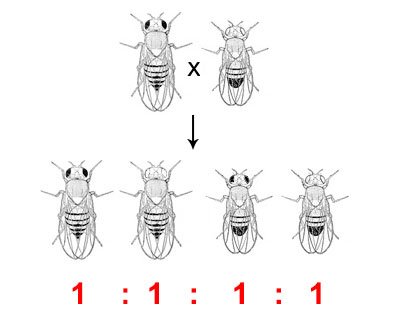
_{Source: Wikimedia Commons contributors, modified}

We got a ratio of one quarter (or 1:1:1:1) for each possibility: male with black eyes, male with white eyes, female with black eyes, female with white eyes.

Only problem is, when Thomas Hunt Morgan did a similar experiment with purple and red-eyed Drosophila flies who had either normal or vestigial (i.e. atrophied, or small) wings, that's not what he saw. His results showed this:

_{Data taken from here}

Now, I'm not great at math, but I can tell when numbers are roughly the same, and that up there doesn't look like a 1 to 1 to 1 to 1 ratio to me.

So what went wrong? Why do those numbers deviate so drastically from the Mendelian prediction?

The Chromosome Theory

Also called the Boveri–Sutton chromosome theory, named after the two fellas who independently proposed it.

What they both noticed was that chromosomes seem to segregate just like Mendel's traits did:

[G]enes are in pairs (so are chromosomes); the alleles of a gene segregate equally into gametes (so do the members of a pair of homologous chromosomes); different genes act independently (so do different chromosome pairs). After recognizing this parallel behavior [...], both investigators reached the same conclusion that the parallel behavior of genes and chromosomes suggests that genes are located on chromosomes. [7]

It isn't so hard to add big As and little As to a schema of chromosomes undergoing meiosis and see that they follow along the same path as Mendel's traits:

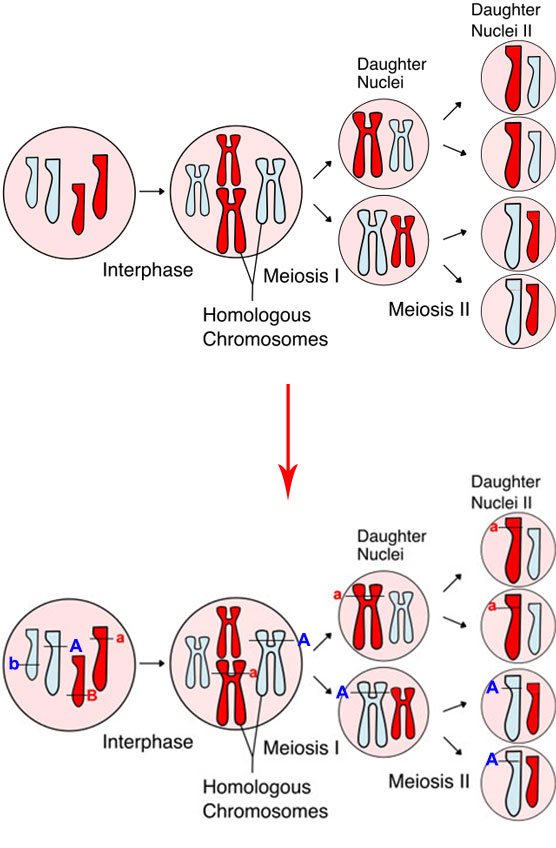
You can do the Bs for homework.

_{Source: Wikimedia Commons contributors, modified}

So the chromosome theory was the idea that these chromosomes (Greek for "colored bodies", because they needed to be stained with dyes to be seen under the microscope) were somehow the carriers of these phenotypic traits.

But then how does the chromosome theory fare any better than Mendel's Law of Independent Assortment, if both give exactly the same results?

Well, Morgan (the fly-breeder) suggested that the traits that show linkage — i.e., the traits that do not follow the Law of Independent Assortment — are located on the same chromosome, so they do not assort randomly. [5]

This chromosome idea explains linkage, and it explains the Law of Independent Assortment: some genes are linked because they are on the same chromosome, and some genes inherit independently because they are on different chromosomes.

So far, so good.

But then, how do you explain traits that are found in neither of the parents, so-called "recombinant traits". In other words, how do you explain traits that are neither always linked, nor always independent, but somewhere in-between?

To explain this, Morgan suggested a process called "crossing-over". [5] It looks something like this:

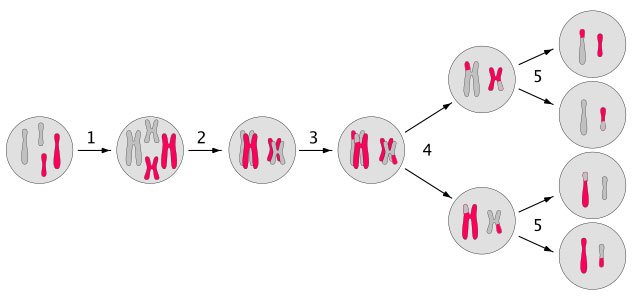
_{Source: Wikimedia Commons contributors}

So, apparently, when the chromosomes lie on top of each other, sometimes they exchange parts.

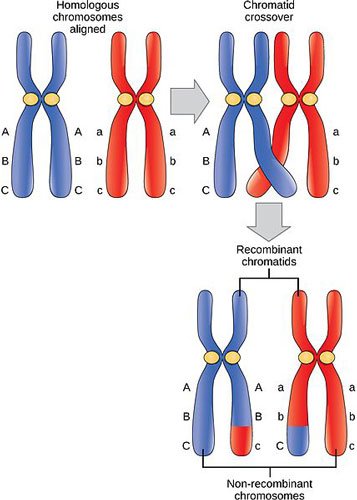
There's a reason they're shaped like an X, with all that hanky panky going on. Here's an animated version (I believe biologists call it hentai, or something) if you're interested.

_{Source: Wikimedia Commons contributors}

_{Source video: Looking at Chromosomes}

This would explain why instead of absolute linkage or absolute independence, we often observe recombinations, where genes are seemingly found on chromosomes where they don't belong.

Now, I don't know about you, but this looks to me like a theory that's made up just to explain the data. Unless we get some kind of testable prediction out of this, it's little more than ad hoc (or as I like to call it, hocwash).

Enter Alfred Sturtevant

Sturtevant was Morgan's student. His name might look like it comes from the word "student" (with hints of "steward" and "servant"), but it in fact means "hasty individual".

Not one to deny the theory of nominative determinism, Sturtevant would come to honor his ancestors' name, in that famously hasty all-nighter.

It began when Morgan (who noticed that different traits showed different recombination frequencies) decided to ask Sturtevant (then an undergrad student) to try and make sense of the data. [1]

See if you can figure out what he did, by studying the following points:

1. If Morgan's "cross-over" theory is correct, then it follows from the laws of mathematics and randomness, that the closer together two genes are on the chromosome, the less chances there are that a recombination event will happen right between them. On the other hand, the farther apart two genes are on the chromosome, the greater the chances that a recombination event will split them. [10]

2. So, the greater the recombination frequency between two traits, the larger their distance must be on the chromosome.

3. Recombination frequencies for many traits, from many animals, were available when Sturtevant was assigned this work. Suppose he pulls the data. Suppose the data shows the following:
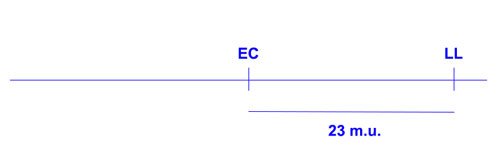
   (a) Eye color and leg length recombination frequency: 23 m.u. (m.u. = chromosome map unit; 1 m.u. = 1% recombination frequency)
   (b) Eye color and wing size recombination frequency: 12 m.u.

So the question is, if these traits have spatial locations (called loci; no relation to Thor's brother) on the chromosome, how can you make testable predictions that can falsify the chromosome theory?

Had a go?

Here's how Sturtevant did it. (For the more complicated version, see here, section "Construction of a Linkage Map".)

Let's start with the eye color, and put it dead center on a line that represents a chromosome.

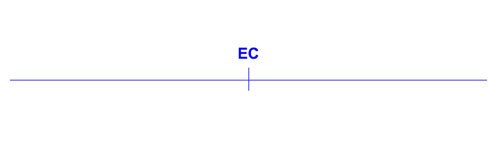
Then, we know from (a), leg length is a certain distance away from eye color. We don't know on which side, but we're only interested in distances right now, not directions.

From (b), we know wing size is 12 m.u. away from eye color:

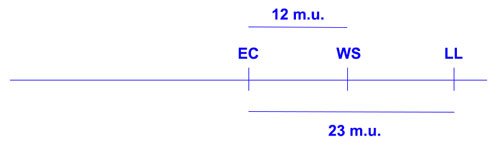
Oh boy, now we got a testable prediction! This is the stuff scientists dream about!

You see, the distance between wing size and leg length can only be either 23 minus 12 (=11), or 23 plus 12 (=35), depending on which side the traits reside on. 11 and 35 are the only two possible numbers. Within reasonable brackets, any other numbers would falsify the chromosome theory.

They didn't. The numbers matched.

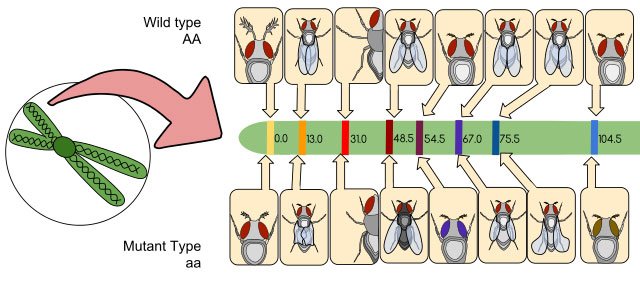
67 - 31 = 36

_{Source: Wikimedia Commons contributors}

Eric Lander called this the most famous all-nighter in the history of genetics, and a former research partner claimed that "modern biochemical genetics stems directly from Sturtevant's work." [6]

To be sure, Sturtevant received the National Medal of Science for this one night's work [6], and the rest of us lived wiser ever after!

Epilogue

What I find fascinating about the above, is that it all happened before DNA was discovered. [7] Yes: people could do gene mapping before they knew what genes were at a molecular level.

Let me repeat that, because it bears repeating: before scientists knew anything about DNA, they could tell you about the spatial location of genes on chromosomes. They could tell you the order in which they followed one another. They could tell you how close they were to each other. They could tell you the chances of a recombination event. Genetics thus became its own sub-discipline, to this day it can hold its head up high and stand as an equal next to molecular biology.

Sturtevant's work became another great example of armchair sciencing, and because of it the chromosome hypothesis was finally accepted. It wasn't always that way:

[T]he Sutton-Boveri [chromosome] hypothesis [...] was a bombshell. The first response to publication of the hypothesis was to try to pick holes in it. For years after, there was a raging controversy over the validity of the chromosome theory of heredity. [7]

You might think scientists are too strict, but I wouldn't have it any other way. After all, it's not called the chromosome theory for nothing: it means it has passed the most rigorous tests the collective human mind can devise.

Before Sturtevant, everything was correlation: there were parallel patterns that showed that genes probably resided in chromosomes, which made the Sutton-Boveri hypothesis attractive to some, but debate raged on. [7] Sturtevant's genenic maps provided the first definitive proof for the chromosome hypothesis — which now finally earned the right to be called a theory.

P.S.

I don't want to leave you thinking the delegating teacher and fly-breeder ever regretted assigning this work to Sturtevant: Thomas Morgan went on to win the 1933 Nobel Prize for his work with fruit flies. [8] This work did not disprove Mendel's Law of Independent Assortment, but it refined it, and paved the way toward a synthesis of genetics with evolutionary theory. [9]

References

1. Griffiths AJF, Miller JH, Suzuki DT, et al. An Introduction to Genetic Analysis. 7th edition. New York: W. H. Freeman; 2000. Linkage maps. Available from: https://www.ncbi.nlm.nih.gov/books/NBK21827/

2. Wikipedia contributors, "Mendelian inheritance," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Mendelian_inheritance&oldid=815201913 (accessed December 17, 2017).

3. Wikipedia contributors, "Thomas Hunt Morgan," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Thomas_Hunt_Morgan&oldid=815006379 (accessed December 17, 2017).

4. Wikipedia contributors, "Boveri–Sutton chromosome theory," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Boveri%E2%80%93Sutton_chromosome_theory&oldid=811712316 (accessed December 17, 2017).

5. Griffiths AJF, Miller JH, Suzuki DT, et al. An Introduction to Genetic Analysis. 7th edition. New York: W. H. Freeman; 2000. The discovery of linkage. Available from: https://www.ncbi.nlm.nih.gov/books/NBK22076/

6. Wikipedia contributors, "Alfred Sturtevant," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Alfred_Sturtevant&oldid=798692384 (accessed December 17, 2017).

7. Griffiths AJF, Miller JH, Suzuki DT, et al. An Introduction to Genetic Analysis. 7th edition. New York: W. H. Freeman; 2000. Historical development of the chromosome theory. Available from: https://www.ncbi.nlm.nih.gov/books/NBK22088/

8. Miko, I. (2008) Thomas Hunt Morgan and sex linkage. Nature Education 1(1):143. https://www.nature.com/scitable/topicpage/thomas-hunt-morgan-and-sex-linkage-452

9. Genome News Network. Thomas Hunt Morgan (1866-1945) establishes the chromosomal theory of heredity. http://www.genomenewsnetwork.org/resources/timeline/1910_Morgan.php

10. Wikipedia contributors, "Genetic linkage," Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Genetic_linkage&oldid=802601194 (accessed December 17, 2017).

11. "Just a Theory": 7 Misused Science Words. LiveScience on April 2, 2013. https://www.scientificamerican.com/article/just-a-theory-7-misused-science-words/

---

Earlier Introduction to Biology episodes:

5: Mendel's Lucky Number Seven — The law of genetics that almost wasn't

4: How Cells Use Logic To Do The Impossible

3 : Armchair Science — The Discovery of Proteins' Secondary Structure

2 : How Cell Membranes Form Spontaneously

1 : Eduard Buchner: The Man Who Killed Vitalism

---

steemSTEM is the go-to place for science on Steemit. Check it out at @steemstem or browse the #steemSTEM tag or chat live at steemit.chat