안녕하세요. 훈하니 @hunhani입니다.

오늘은 멱 법칙과 레비 안정 분포로 알아보는 빈익빈 부익부에 대해 살펴보겠습니다.

대문을 제작해주신 @leesol 님께 감사드립니다.

자기유사성의 프랙털 구조

브누아 망델브로는 신호와 잡음 사이의 관계를 연구하면서 그 사이에 일정한 구조가 존재한다는 것을 깨달았습니다. 이 구조는 일부 작은 조각이 전체와 비슷한 (자기유사성) 기하학적 형태를 갖고 있었습니다. 망델브로는 이러한 구조를 그가 1975년에 발간한 The Fractal Geometry of Nature를 통해 프랙털(Fractal)이라는 용어로 명명하였습니다. 이후 자연계가 통계적인 프랙털 모양을 하고 있다는 사실이 밝혀지면서 학자들이 프랙털을 카오스 이론에 접목시켰고 현재까지도 자연을 분석하고 예측하는데 있어 굉장히 유용하게 사용되고 있습니다. 프랙털은 구름, 산, 번개, 난류, 해안선, 나뭇가지 등 자기유사성을 갖는 여러 자연물에서 나타날 분만 아니라 수학적 분석, 생태학적 계산, 위상 공간에 나타나는 운동모형에 적용됩니다. 심지어 주식의 변동 곡선까지도 하루, 한 주, 한 달, 일 년 사이의 변화가 서로 비슷한 형태로 나타나는 프랙털 구조를 갖는데요. 이처럼 프랙털을 이용하면 불규칙하며 혼란스러워 보이는 현상 속에서도 일정한 규칙을 찾아낼 수 있답니다.

망델브로의 직관력

표준적인 금융 이론에서 가격은 로그 정규분포, 수익률은 정규분포를 따릅니다. (Chapter 3. 천체물리학자가 파헤친 주가와 주가 수익률의 관계 참조) 그런데 망델브로는 시카고 상품 거래소의 면화 거래 정보를 보자마자 직관적으로 가격이 멱 법칙이 성립하는 레비 안정 분포를 따른다는 것을 깨달았습니다. 이를 계기로 망델브로는 면화와 같은 기타 원자재들은 물론 주식, 외환, 채권 등 다양한 금융 자산 모두가 예외 없이 레비 안정 분포를 갖는다는 사실을 발견했습니다. 이 연구 결과가 발표되자마자 경제학계는 엄청난 관심을 보였지만 얼마 지나지 않아 망델브로의 연구는 경제학계 내에서 일종의 금기가 되어버리는데요. 이는 금융 변수들이 레비 안정 분포를 따른다는 사실을 인정하게 되면, 자산 수익률의 표준편차가 무한대가 되어버린다는 모순 때문이었습니다. 이러한 모순은 당시 경제학계가 내세우고 있던 포트폴리오 이론을 비롯한 금융학 성과를 무의미하게 만들어서 경제학계는 도저히 받아들일 수 없었던 것이죠. 이에 염증을 느낀 망델브로는 경제학에서 손을 떼고 프랙털 기하학을 정립하는데 신경을 집중하게 되었습니다. 덕분에 프랙털 기하학 분야를 고안하는 큰 업적을 이루었지만 경제학계 입장에서 보면 대성할 수 있는 금융 이론의 샛별을 외면한 셈입니다.

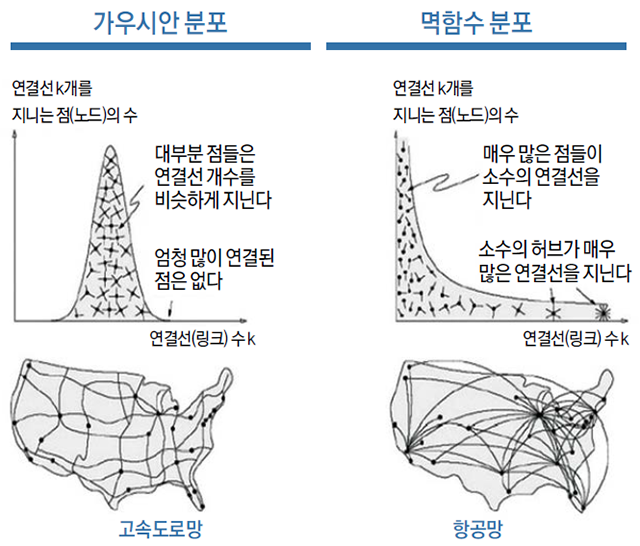
멱 법칙이란?

멱 법칙(Power law)은 한 수가 다른 수의 거듭제곱으로 표현되는 두 수의 함수적 관계를 의미합니다. 가령, 특정 인구수를 가지는 도시들의 숫자는 인구수의 거듭제곱에 반비례하여 나타나게 되죠. 뿐만 아니라 매우 다양한 분야에서 하지만 지극히 제한된 범위에서 근사적으로 멱 법칙이 성립하는 사례를 찾아볼 수 있습니다. 지진의 강도, 달의 크레이터, 태양 플레어, 다양한 종의 사냥 패턴, 신경 개체군 활동 패턴의 크기, 대다수 언어에서 단어의 사용 빈도, 성씨의 빈도, 유기체의 계통 분기군의 종의 다양성, 정전, 전쟁 등이 그에 해당합니다. 다만, 모든 값이 멱 법칙을 따르는 분포는 상당히 드물며, 대부분 분포의 꼬리 부분에서만 멱 법칙이 적용되지요. 예외적으로 다양한 복합 매질에서 발생하는 음파 감쇠의 경우 넓은 주파수 대역에 걸쳐 멱 법칙을 따른답니다.

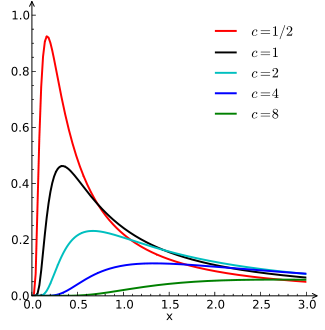
레비 안정 분포란?

19세기 수학자 오귀스탱 루이 코시의 코시 분포 (Cauchy distribution)는 정규분포와 비슷하게 좌우 대칭으로 나타나게 되지만 중앙값과 최빈값만 정의되고 평균값과 표준 편차가 무한대로 계산되어 아예 정의할 수가 없습니다. 마찬가지로 20세기 수학자 폴 레비(Paul Levy)가 고안해 낸 레비 안정 분포(Levy stable distribution) 역시 표준 편차가 무한대가 되는 특징을 가지는데요. 레비 안정 분포의 매개변수를 α라고 하며 α가 2인 경우에만 정규분포가 되고 그 외의 경우에는 보통의 레비 안정 분포가 됩니다. 즉, 19세기 수학자 카를 가우스의 이름을 따서 가우스 분포(Gaussian distribution)라고도 불리는 정규분포는 사실 레비 안정 분포의 특수한 경우에 해당하는 것입니다. 망델브로가 레비 안정 분포를 찾게 된 첫 금융 자산인 면화 가격의 경우 α가 1.7정도에 불과했습니다. 망델브로의 주장대로 모든 금융 변수들이 레비 안정 분포를 따른다면, 자산 수익률의 표준편차가 무한대가 되어버리는 모순이 있다고 말했었죠? 이후 50여 년에 걸친 후속 연구를 통해 모든 금융 변수에 레비-안정 분포가 적용되지 않는다는 결론이 받아들여지고 있으나 망델브로의 주장은 금융 시장이 무작위적일 경우 단순히 통계학적 도구를 사용하여 시장을 분석할 수는 없음을 다른 방식으로 제시한 것이라 큰 의의가 있습니다.

빈익빈 부익부

망델브로의 주장이 모든 경우에 성립하는 것은 아니지만, 주가나 환율 같은 금융 변수들이 정규분포가 아닌 멱 법칙의 지배를 받고 레비 안정 분포를 따르는 경우가 실제로 발생합니다. 예를 들어, 전 세계 70억 인구의 재산이 정규분포를 따른다면 워렌 버핏, 빌 게이츠, 카를로스 슬림 등과 같은 인물들이 절대 나올 수 없어야 하지만 실제로는 그렇지 않죠. 정규분포에 따라 재산이 균등하게 분배되기보다는 레비 안정 분포에 따라 한 쪽에 쏠리고 있는 셈입니다. 멱 법칙 및 레비 안정 분포는 빈익빈 부익부가 성립하는 것을 보여줍니다. 부와 소득은 하한선이 있는 반면 상한선이 없죠. 가령, 사람이 가질 수 있는 재산의 하한선은 빈털터리, 다시 말해 0입니다. 마이너스 재산이란 것은 없습니다. 심지어 빚이 발상해서 재산이 잠시 마이너스가 될 수도 있지만 본인이 파산 신청을 하면 잔여 빚이 어느 정도 정리가 되니 궁극적으로 재산이 마이너스가 될 수는 없습니다. 반면, 재산의 상한선은 없으므로 통계적으로 누군가는 어마어마한 부와 소득을 갖게 될 수 있습니다. 이처럼 자연계에는 정규분포가 아닌 멱 법칙 및 레비 안정 분포를 따르는 경우가 종종 있어 우리가 정규분포에 의해 예측하는 것보다 실제로 극단적인 일들이 발생할 수 있음을 암시합니다. 특히, 금융 시장에는 비이성적으로 보이는 폭등, 갑작스러운 폭락이 이에 해당하겠지요.

다음 편을 기대해주세요!

지난 이야기

본문에서 사용된 모든 이미지는 구글 이미지에서 가져왔음을 밝힙니다.
본문을 작성하는데 있어 주식투자는 두뇌게임이다, 돈의 물리학, 금융의 물리학, 위키피디아 내용을 참조하였습니다.

[돈을 지배하는 물리 법칙] Chapter 4. 멱 법칙과 레비 안정 분포로 알아보는 빈익빈 부익부