
With the last two articles of this series (that are now already old as I am a slow writer), I described some phenomena that could not be explained with the help of what was called classical physics at the end of the 19th century / beginning of the 20th century. Those were consisting of atomic spectra and black body radiation.
In particular, I have introduced in the last post the famous Planck constant (the constant associated with quantum mechanics) and detailed the black body radiation interpretation of Planck: the atoms of a cavity (assimilated to a black body) radiate discrete amounts of energy, equivalently known as energy quanta.
In this post, I will detail the work of Einstein (that granted him his Nobel prize) where he showed that the interpretation of Planck was incorrect. Energy quantization is not a property of the black body, but a property of any radiation, and allowed us to understand and explain the photoelectric effect observed by Hertz at the end of the 19th century.
WHEN EINSTEIN MEETS PLANCK
In 1905, Einstein reanalyzes the interpretation of the black body made by Planck. He starts from the idea that a radiation can only exist under the form of a discrete amount of energy quanta, each energy quantum being proportional to the radiation frequency.
[image credits: Wikipedia]
This idea is very similar to the one of Planck, but with one major difference. The energy of each quantum E is proportional to a frequency. But in contrast to Planck, it is this time the frequency of the radiation itself ν,
E = h ν,
and is not related to the black body cavity anymore. The black body can hence be seen as containing a radiation in equilibrium.
The major advance with respect to Planck is that the formula above is now a general property of any electromagnetic radiation, and not a property of a black body only.
Sometimes, the above equation is rewritten in terms of the wavelength 𝝀 or the angular frequency ɷ of the wave.
E = ℏ ɷ = h c / 𝝀.
All the above equations are connected by the fact that the frequency of the wave
ν = c / 𝝀 = ɷ / (2π),
Both the two constants h and ℏ (= h / 2 π) are traditionally called the Planck constants, but the second one (ℏ) yields simpler results.
THE PHOTOELECTRIC EFFECT IN A NUTSHELL
[image credits: Wikipedia]
So far there is nothing very special with the interpretation of Einstein, except that he used it to explain the photoelectric effect observed by Hertz in 1887.
This was a challenge that classical physics was not capable to solve and one of the great successes that paved the way to the idea that radiation was quantized.
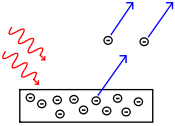
The photoelectric effect originates from the exposure of a metal to light. In other words, it arises when a light source radiates light of a given frequency ν towards a metallic plate. The plate can then emit electrons. However:
[image credits: home-made]
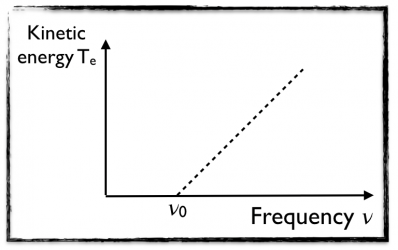
- Electrons are only emitted if the frequency is greater than a specific threshold frequency ν0 that depends on the type of metal under consideration.
- The number of emitted electrons is proportional to the radiation intensity I.
- The kinetic energy of the electrons Te is independent of the the intensity I but varies linearly with the frequency ν.
All of this is illustrated on the figure on the right.
THE PHOTOELECTRIC EFFECT REVISITED BY EINSTEIN
I will now move on with detailing what Einstein explained. The explanation he proposed relies on energy conservation and on the fact that light contains quanta of energy.
As said above, each quantum of energy E is proportional to the radiation frequency ν,
E = h ν,
the constant of proportionality h being the Planck constant. On the other hand, an electron is bounded to the metal with a certain binding energy. The conclusion is straightforward. Only a single quantum can extract an electron from the metal.
If the energy quantum has an energy below the binding energy, it is not energetic enough and nothing moves.
If the quantum has an energy above the binding energy, a part of the energy equal to the binding energy will be used to extract the electron from the metal and the difference will be transformed in electron kinetic energy.
AGAIN BUT WITH EQUATIONS

[image credits: Quantum diaries]
Writing this under the form of an equation, one finds:
Te = h ν - W ,
where W is the energy to be provided for extracting an electron from the metal. The actual value of W depends on the metal species and is in general of the order of a few eV.
We can easily connect W to the threshold frequency ν0 introduced above,
W = h ν0
In the case where the radiation frequency ν is larger than ν0, the energy of the quantum is large enough to balance the electron binding energy and extract the electron it from the metal. Otherwise, it cannot do it. The part of the quantum of energy that is not used to extract the electron is then converted in kinetic energy.
All of this has been verified experimentally. Measuring the slope of the obtained straight line (see the picture above) allows one to extract the value of the Planck constant. The magic here is that the proportionality constant appearing in the study of the photoelectric effect is the same constant as the one arising the the problematics of the black body.
THE IDEA OF A PARTICLE OF LIGHT

[image credits: phys.org]
The story is not finished yet. In 1909, Einstein stroke back and proposed a relation that gives to the quanta of energy all the properties of a particle,
p = ℏ k
where the boldface character indicates tridimensional vectors. k the wave vector of the light wave and p denotes its momentum. The direction of k is the direction of propagation of the light wave and its norm k is called the wave number that is inversely proportional to the wavelength,
k = 2 π / 𝝀.
What is really funny is that in all the relations shown in this article, two of them use the same proportionality constant.
p = ℏ k and E = ℏ ɷ
Those two relations are extremely important. They show that the Planck constant is the proportionality constant linking the mechanical properties of a particle of light and its wave properties.
PHOTONS
It is rather easy to show that the wave number k and the angular frequency ɷ are related by the dispersion relation
ɷ = k c
which yields
E = p c.
This is the relativistic equation for the energy of a massless particle of momentum p. The particles of light are thus massless particles. This is key consequence.
The concept of the existence of a particle of light has been fully accepted only 15 years later, when Compton has discovered the Compton effect confirming that light could behave as a particle. But this is the topic of my next post.
SUMMARY
In this post, I have discussed the analysis of the black body results of Planck by Einstein, and how he proposed that any electromagnetic radiation was quantized. Any radiation only exists as discrete amounts of quanta of energy.
A bit later, Einstein moved further and introduced the concept of a particle of light, that was hard to accept at that time.
In my next post, I will discuss how this particle was observed by Compton and discuss a little bit more the wave-particle duality for the light.
REFERENCES AND TOC
All the material in this post (and the other ones of the series) is extracted from the lectures I have given on this topic since half a decade, and from my book.
For more information on the photelectric effect, the wikipedia page is actually a good start. There are nice links on the bottom of the page one may want to follow.
You can find below the table of contents of this series of posts (thanks @wingz for the suggestion).
I. Introduction
1. Concepts and fundations
2. Interactions and conservation laws
3. Systems of particles
II. The origins of quantum mechanics
1. Fundamental physics at the beginning of the 20th century
2. The mysteries of the atomic spectra
3. The mysteries of the black bodies
4. Quantization of the electromagnetic radiation and the birth of the photons (this post)
