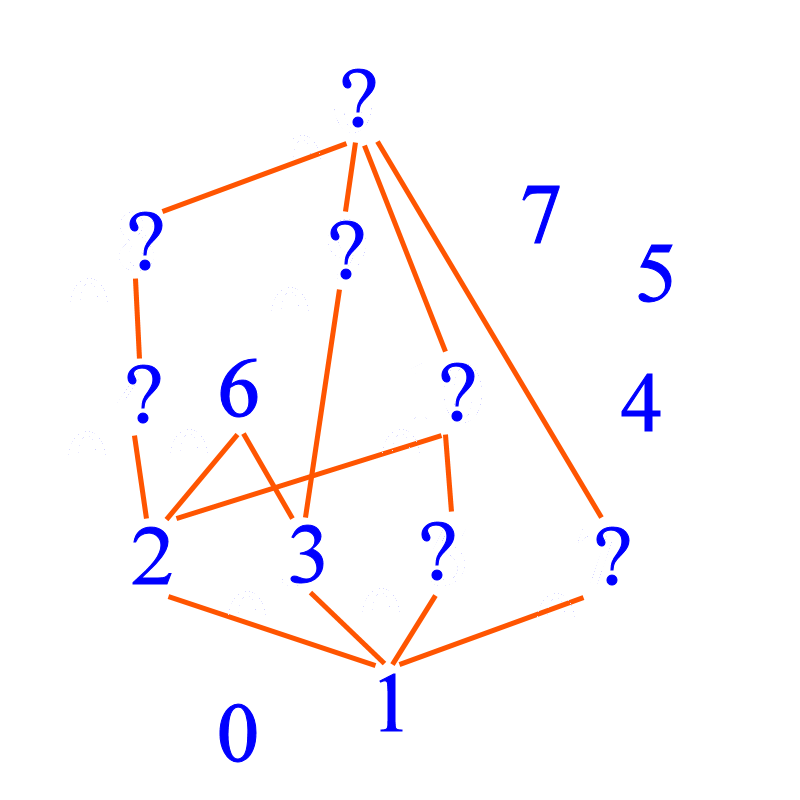
In yesterday's article, I issued a challenge to draw a Hasse diagram for the divisibility relation for the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10.
I also asked these questions to prod i.e. STEEM-u-late your thinking:-
Where would prime numbers fit into the diagram?
Where would the number 1 fit into the diagram?
Where would the number 0 fit into the diagram?
Is it always true that whenever x is a factor of y, x must be smaller than y? Is/are there any exception(s) to this “rule”?
Let us start by noting that the number 1 divides every number. Any number can be divided by 1, e.g. 2 ÷ 1 = 2 i.e. the result is an integer. So 1 is a factor of every number. So I write '1' at the bottom of the diagram.
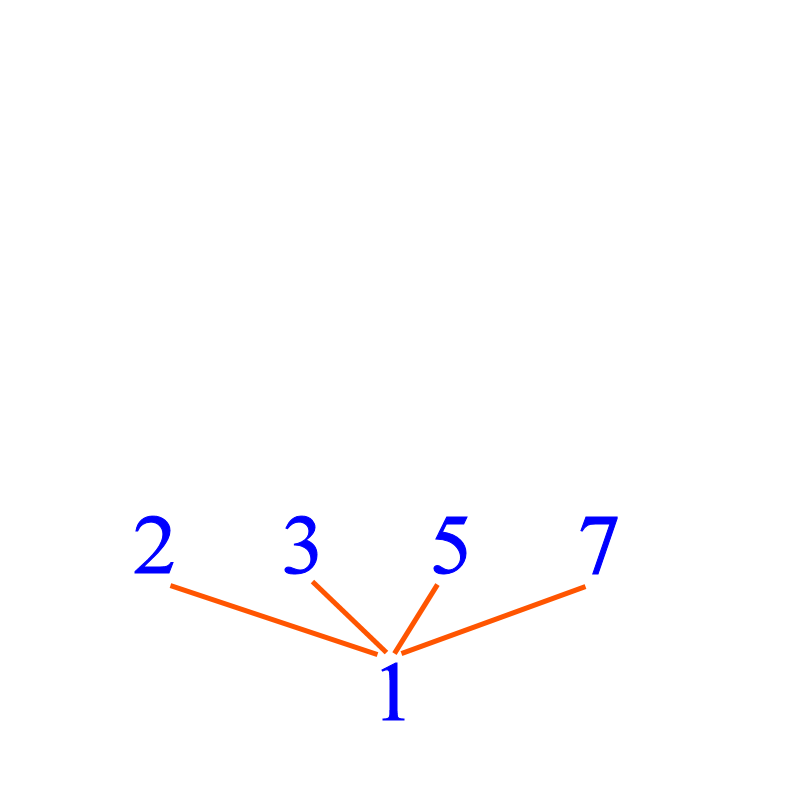
Prime numbers are whole numbers greater than 1 that can only be divided itself and 1. Apart from 1, prime numbers are usually factors of other numbers and are the multiplicative building blocks of whole numbers, just like atoms are building blocks of molecules. So I put the prime numbers 2, 3, 5 and 7 in the row above 1, and join them with 1.
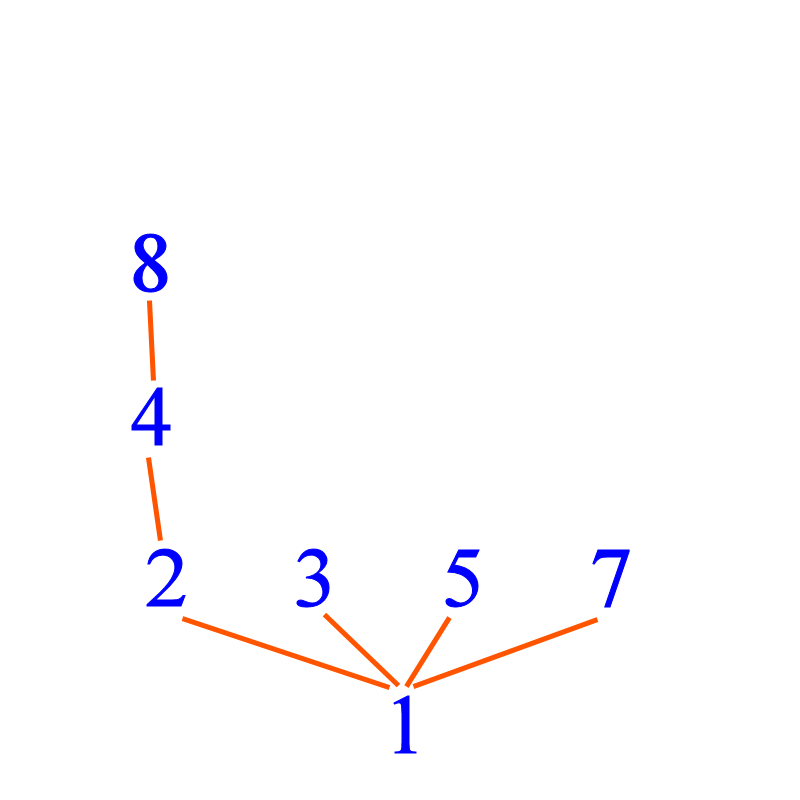
Since 2 | 4 and 4 | 8 we can extend a branch of this "tree" from 2.
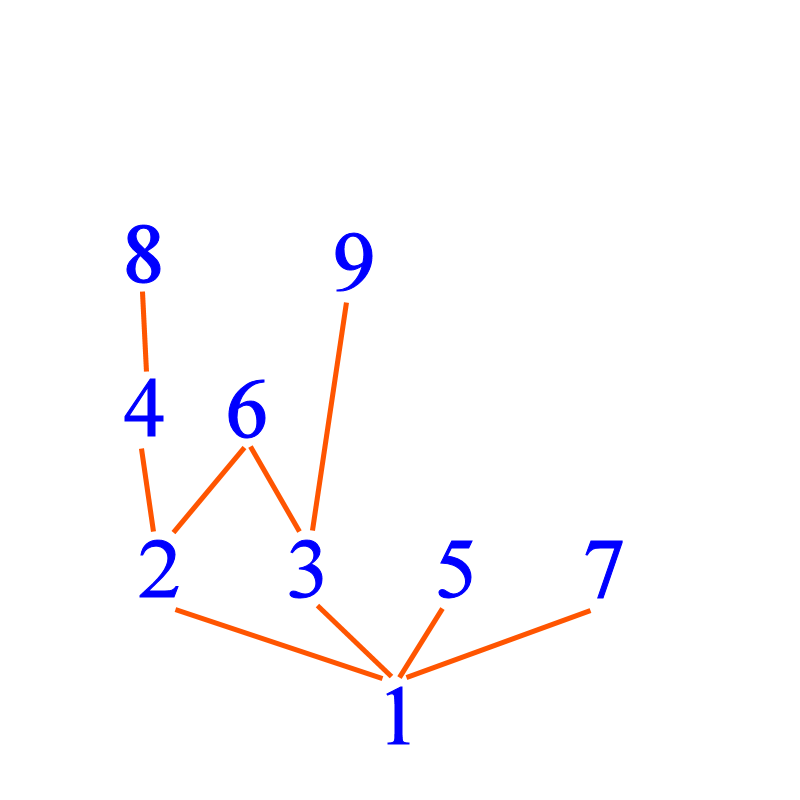
We can also extend the "tree" from three. We know that 3 | 9. The LCM of 2 and 3 is 6, so we have 6 above 2 and 3 and joined to them.
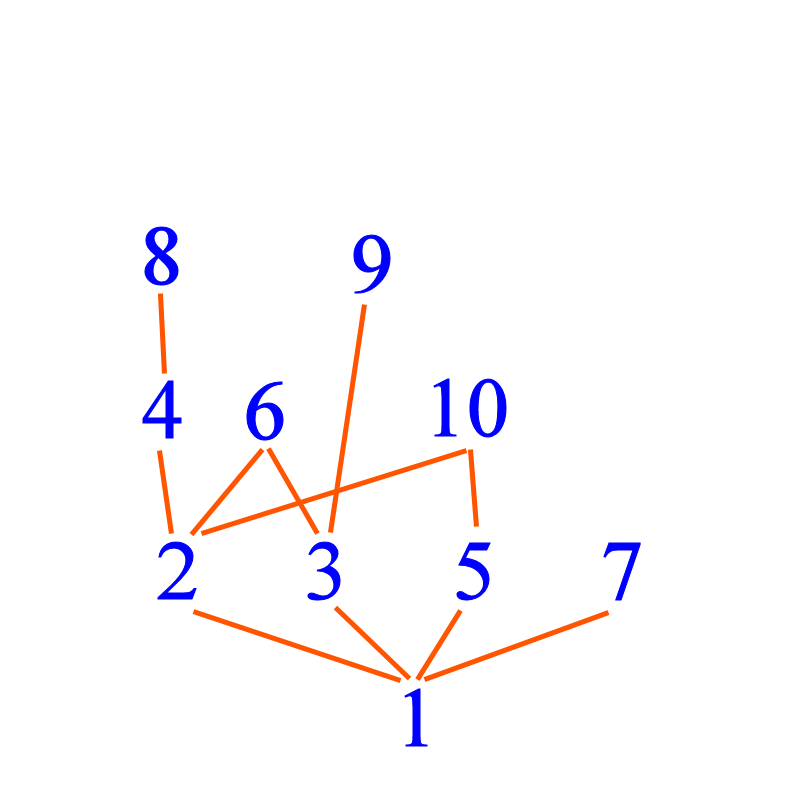
10 is the (lowest) multiple of 2 and 5. Now we are almost done. The question is: where do we put the 0?
(A) Is 0 a factor of any number other than itself?
(B) Is 0 a multiple of any number other than itself?
To answer these questions, let us recap what we mean by "factor" and what we mean by "multiple".
So for example 3 | 6. 3 is a factor of 6. 6 is a multiple of 3. In other words 3 divides 6 or 6 can be divided (into equal whole-number shares) by 3. 6 ÷ 3 = some integer viz. 2.
Definition: We say a | b i.e. a is a factor of b or b is a multiple of a iff there exists an integer c such that a × c = b.
Using this definition, 0 | 0 i.e. 0 is a factor of 0 and 0 is a multiple of 0, This is because 0 × 1 = 0 (put a = 0, c = 1 or any number, and b = 0).
However, the answer to (A) is "no". 0 is not a factor of any non-zero number. In the equation a × c = b, if a = 0 and b is a non-zero number, the equation will always be false no matter what value c is, because the Left Hand Side is always zero whereas the Right Hand Side is not. So it is not possible to have 0 | b where b is a non-zero number. The upshot of this is that the 0 is not going to appear the the bottom of the Hasse diagram.
The answer to (B) is "yes"! In fact, 0 is the multiple of every number! Why? In the equation a × c = 0, no matter what a is, we can always find a number c to multiply it to make it 0. For example c = 0. This always works! Another way of thinking about this is: Say you have 0 bowls of porridge to be shared among, say, 789 monks, each monk gets 0 bowls of porridge.
Since 0 is a multiple of every number, 0 should appear at the top of the diagram. To keep the diagram less messy, I do not explicitly join every possible divisibility relation. Some relations are implied by the transitive law, which says that if x is a factor of y and y is a factor of z, then x is a factor of z. So although 2 | 8, i do not explicitly connect 2 and 8. This connection is implied by transitivity since 2 | 4 and 4 | 8, so it is understood that 2 | 8. You may regard 2 as joined to 8 via 4.
Hence, I join 6, 7, 8, 9, 10 to 0, but it is understood that every number is joined to 0, either directly or indirectly, and I get the following.
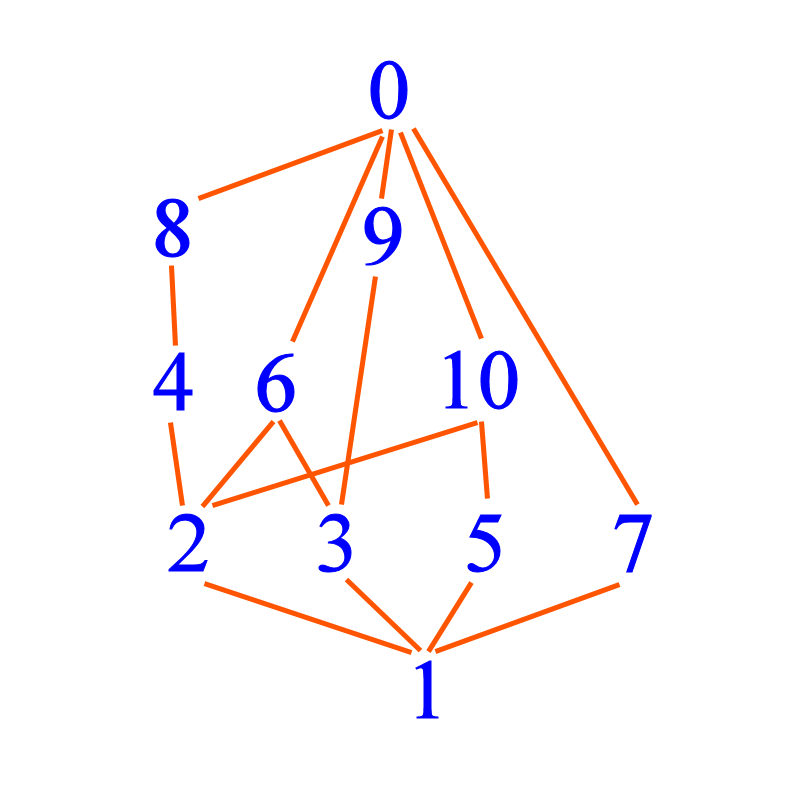
Note that for our numbers, which are non-negative, factors (appearing at lower rows) are usually smaller in magnitude. 0, the number right on top, is the exception. So how do we make a precise mathematical statement for this? We say:
For any non-negative integer a, we have a | 0.
AND
For any b that is a (non-zero) positive integer, a | b implies that a < b.
That it for this article. I hope you found this discussion educational and fun!
cheers!
Announcements
There is still time to join my mathematics contest. SBD to be given away!
Please read my recent posts:
- Exploring HCF (GCD) and LCM with Hasse Diagrams
- Finding HCF and LCM via the Reduced Fraction
- A Fun New Way to find Lowest Common Multiples (LCM)
If you find my articles useful or interesting, please upvote and resteem them! See you tomorrow! Thanks to everybody for your support!!!
@tradersharpe
-- promoting sharp minds
