안녕하세요. 훈하니 @hunhani입니다.

오늘은 연주 시차와 별의 밝기-거리 관계에 대해 살펴보겠습니다. @oldstone 님께 천체물리학을 쉽게 설명해주는 글을 부탁받았습니다. @oldstone 님께 이번 시리즈를 헌정합니다.

대문을 제작해주신 @leesol 님께 감사드립니다.

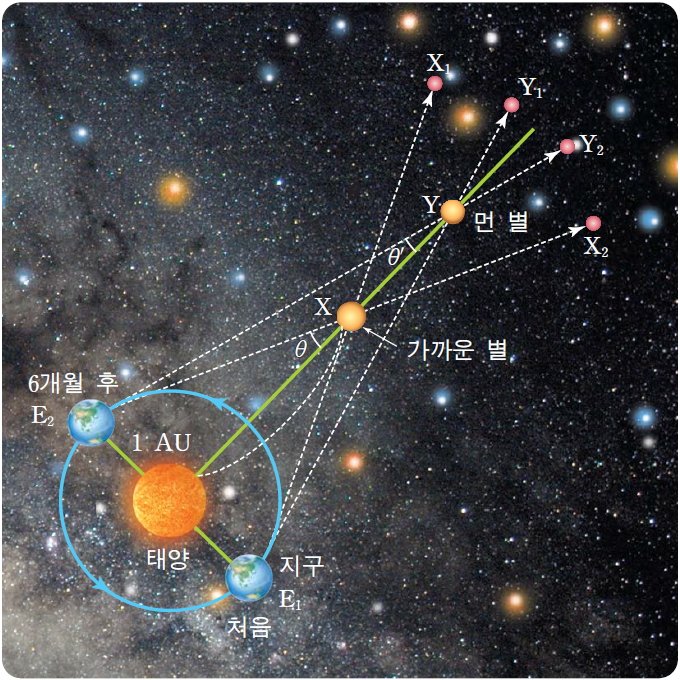
연주 시차

물체의 원근을 느낄 수 있는 이유가 뭘까요? 바로 물체를 볼 때 양쪽 눈에서 시차가 생기기 때문입니다. 천문학에서는 이와 같은 시차의 일종인 연주 시차를 이용하여 별까지의 거리를 구한답니다. 연주 시차는 어떤 천체를 바라보았을 때 지구의 공전에 따라 생기는 시차를 의미합니다. 지구 공전의 결정적 증거라고 할 수 있죠. 연주 시차는 태양과 바라보는 천체를 잇는 직선, 그리고 지구와 바라보는 천체를 잇는 직선이 이루는 각으로 나타냅니다. 따라서 실제 시차와는 절반의 차이가 나니 유념해야 합니다. 그림에서 보다시피 연주 시차가 클수록 지구와 가까운 별이랍니다.

천문학에서 사용하는 거리 단위

1 AU(천문 단위) : 태양과 지구 사이의 평균 거리 = 1.496 × 10^8 km
1 ly(광년) : 빛의 속도로 1년 동안 움직이는 거리 = 9.46 × 10^12 km
1 pc(파섹) : 연주 시차가 1″인 별까지의 거리 = 3.086 × 10^13 km = 3.26 ly

연주 시차와 가까운 별의 거리

연주 시차를 통해 해당 천체와의 거리를 구할 수 있습니다. 그러나 대부분의 별은 매우 멀리 있어 연주 시차가 아주 작아서 지구의 대기 산란 효과 등의 방해 요소에 의해 미세한 연주 시차는 계산하기 힘듭니다. 따라서 연주 시차를 통해 천체와의 거리를 구하는 것은 매우 제한적이며 상대적으로 가까운 별들의 거리만 잴 수 있다는 단점이 있죠. 일반적으로 지구에서 최대 100 pc(파섹) 정도 이내에 있는 별의 거리를 구하는데 연주 시차가 이용됩니다.

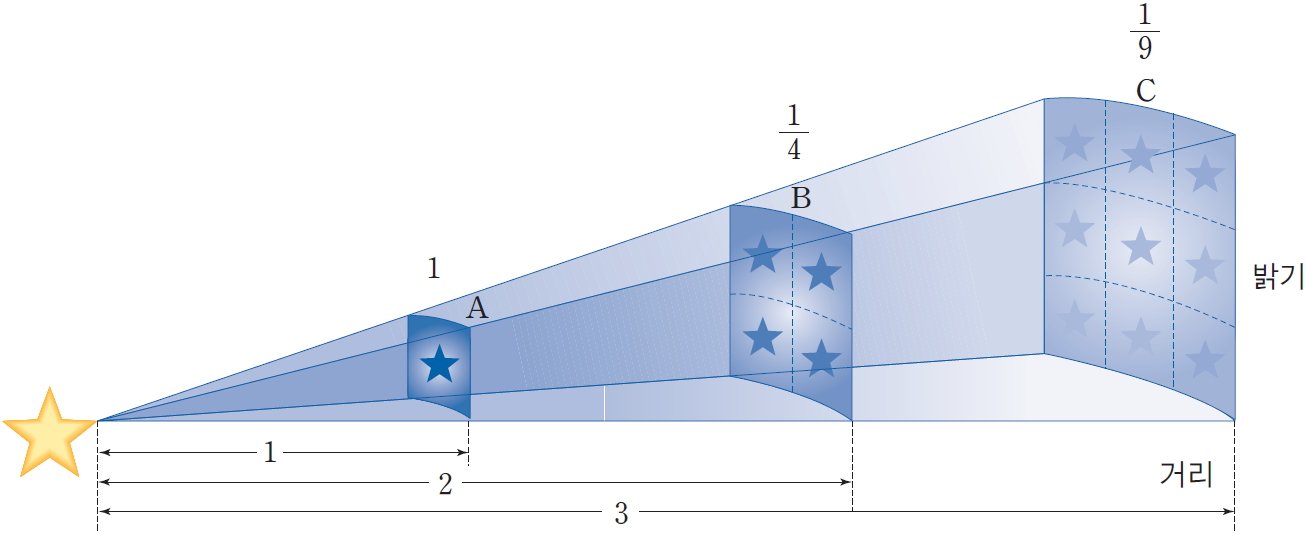
먼 별의 거리를 구하려면?

별의 거리가 100 pc(파섹) 이상 멀어지면 연주 시차를 이용한 방법으로는 측정의 오차가 너무 커지기 때문에, 더 멀리 있는 별들까지의 거리를 측정하려면 다른 방법을 이용해야만 합니다. 이 경우 포거슨 방정식 및 허블 공식을 통해 별의 거리를 구하는데요. 오늘은 별의 밝기와 거리 관계를 이용한 포거슨 방정식에 대해 집중적으로 알아보겠습니다.

겉보기 등급과 절대 등급

포거슨 방정식에 대해 이야기하기 전에 별의 밝기 등급을 먼저 알아보겠습니다. 별의 밝기를 눈에 보이는 대로 나타낸 것을 겉보기 등급이라고 합니다. 값이 작을수록 밝게 보이는 별이죠. 주요 천체들의 겉보기 등급은 다음과 같습니다. [태양: -26.7, 보름달: -12.9, 금성 (최대 밝기 기준): -4.6, 목성&화성 (최대 밝기 기준): -2.9, 수성 (최대 밝기 기준): -1.9, 시리우스: -1.4, 북극성: 2.0] 그런데 겉보기 등급이 큰 어두운 별의 경우 이 별이 실제로 어두운 별이라서 어둡게 보이는 것인지, 실제 밝기는 밝은데 너무 멀리 있어서 어둡게 보이는 것인지 알 수 없습니다. 따라서 별의 실제 밝기를 비교하기 위해서는 모든 별을 같은 거리에 둔 상태에서 비교해야 하는데, 모든 별을 10 pc의 거리에 옮겨 놓았다고 가정했을 때의 별의 밝기 등급을 절대 등급이라고 합니다. 거리가 r(pc)인 어떤 별의 겉보기 등급을 m, 이 별의 절대 등급을 M이라고 놓으면, 포그슨 방정식으로부터 다음과 같은 관계식을 얻을 수 있는데요. 여기서 m-M은 별의 거리를 나타내는 척도란 의미에서 거리 지수라고 일컫습니다. 겉보기 등급과 절대 등급의 차이가 클수록, 즉 거리 지수가 큰 별일수록 지구로부터 멀리 떨어져 있는 별이지요. 따라서 어떤 별의 겉보기 등급과 절대 등급을 안다면 별까지의 거리를 구할 수 있습니다.

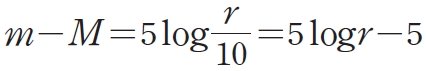
포거슨 방정식

1856년 영국의 천문학자 포거슨은 빛의 측정 장치를 이용하여 1등급의 별이 6등급의 별보다 100배 더 밝다는 사실을 통해 1등급마다 약 2.5배의 밝기 차이가 나는 것을 알아냈습니다. 포거슨은 여기에 별의 밝기는 거리의 제곱에 반비례한다는 사실을 토대로 별의 밝기를 정량적으로 나타내는 관계식을 만들었고 이 관계식을 그의 이름을 따 포거슨 방정식이라고 명명했습니다. 겉보기 등급이 각각 m1, m2인 두 별의 밝기를 각각 l1, l2라고 하고, 두 별까지의 거리를 각각 d1, d2라고 하면 두 별의 등급과 밝기 사이에는 아래와 같은 관계식(포거슨 방정식)이 성립합니다. 포거슨 방정식을 사용하면 어떤 별의 실제 밝기를 알고 있을 경우, 별의 실제 밝기에 대한 겉보기 밝기의 비를 계산하여 별까지의 거리를 구할 수 있습니다.

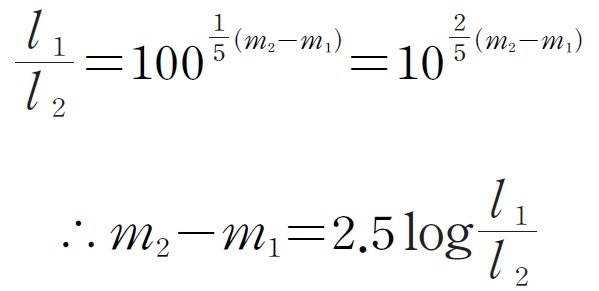
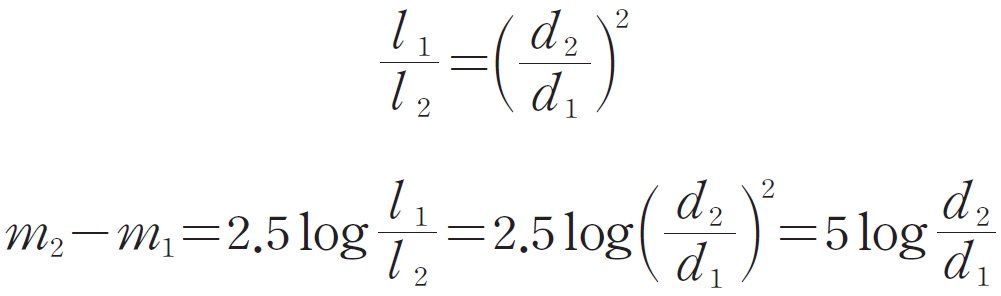
다음 편을 기대해주세요!

지난 이야기

본문에서 사용된 모든 이미지는 구글 이미지에서 가져왔음을 밝힙니다.
본문을 작성하는데 있어 천재학습백과, 위키피디아, ZUM 학습백과 내용을 참조하였습니다.

[밤하늘의 물리학] Chapter 3. 연주 시차와 별의 밝기-거리 관계