
I am very happy to restart today my Steemit quantum mechanics lecture series. The 7 previous episodes can be found at the end of this post.

[image credits: Wikipedia]
In my last article, I mentioned, at the very end of the post, that Einstein introduced the concept of particles of light, or of photons (please click here for a little reminder).
At that time, there was no experimental proof of it, although we today know this is for real.
This fact was in fact only fully admitted by the scientific community 15 years later, with the corresponding experimental evidence brought by Arthur Compton in 1923.
This is by the way the guy shown on the right, who got the Nobel Prize in physics for this discovery a couple of years later.
CONTEXT AND EXPERIMENTAL SETUP
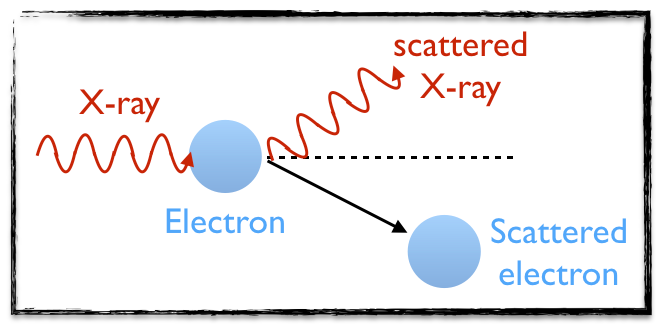
[image credits: homemade]
In the 1920ies, Compton was studying the properties of X-rays sent through a target made of graphite or pyrex. This is illustrated on the picture on the left.
We have an incoming X-ray (in red, on the left-hand side of the picture) that hit an electron (the first blue circle on the picture) of the target material. As a result, the outgoing X-ray and electron are scattered away at some angle with respect to the initial direction.
As the energy of the initial X-ray is much greater than the binding energy of the electron extracted from the target, this experiment can be seen as the bombardment of a free electron with light.
Taking classical electromagnetism, the wavelength of the initial X-ray has to be equal to the wavelength of the scattered ray.
This is however not what was observed in multiple experiments where the scattered ray wavelength was often found larger than the initial one.
A SIMPLER MODELIZATION OF THE PUZZLING RESULTS
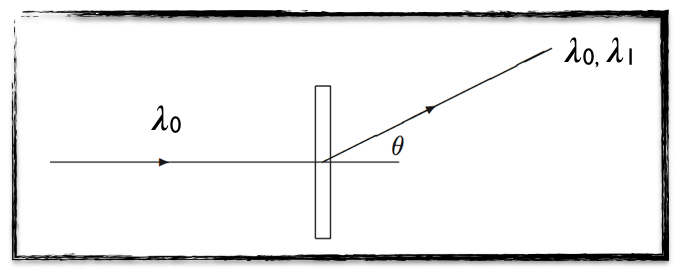
[image credits: homemade]
Let us first make a simple modelization of the Compton experiment. This is illustrated on the picture on the right.
We have here one incoming X-ray with a wavelength equal to λ0.
After hitting the target (the rectangle on the middle of the picture), the X-ray is deviated by some angle θ and its wavelength changes.
Analyzing the possible values taken by this wavelength, it was observed that the resulting distribution was constituted of two components, a first one around the initial wavelength λ0 and a second one around a larger wavelength λ1.
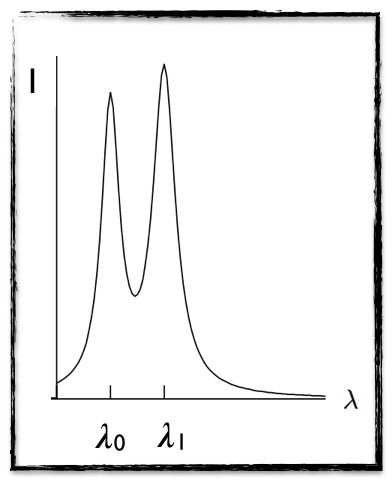
[image credits: homemade]
On the picture on the left were one shows the results of a possible Compton experiment.
One clearly observes the two peaks centered on the λ0 and λ1 wavelengths.
The reason why we have Gaussian peaks is due to the fact that is impossible to produce radiation with a well-defined wavelength. We always get some distribution around a most probable wavelength value.
What was missing at that time was the explanation for the second peak.
WHEN COMPTON USE EINSTEIN PROPOSAL
[image credits: Wikipedia]
As said in my previous post, Einstein proposed in 1905 the concept of a particle of light carrying a quantum of energy proportional to the photon frequency.
Compton used this idea in 1923 to provide an explanation to the so-far not-understood outgoing X-ray wavelength distribution.
He interpreted the above result as the outcome of a collision between a particle of light (or a photon) and an electron at rest.
A fraction of the photon energy is then transferred to the electron, so that the latter is extracted from the material of the target (the binding energy is negligible, as said above) and starts to live its life.
Coming back to our photon, it has in this way lost some energy. As shown here, there is a relation between a photon energy (E) and its wavelength (𝝀): E = h c / 𝝀 (where c is the speed of light). This means that the energy is inversely proportional to the wavelength.
A photon that looses energy will hence get a larger wavelength. That is qualitatively what is happening and why we got a second peak.
HOW WOULD THE EQUATIONS BE DERIVED

[image credits: Quantum diaries]
I will not work out in details all the equations, but instead give the basic ideas behind the calculation of the Compton scattering formula.
Let us consider a collision of an initial photon and an initial electron that will produce a final photon and a final electron.
The starting point is to use energy and momentum conservation: the sum of the energies of the initial particles equals the sum of the energies of the final particles, and the sum of the momenta of the initial particles equals the sum of the momenta of the final particles.
Special relativity and the proposal of Einstein for the photon properties then help:
- the photon energy (E) is connected to its frequency (ν): E = h ν;
- the photon energy (E) is connected to its momentum (p) : E = p c;
- the initial electron energy Ee equals its rest mass (as this guy is at rest): Ee = me c2;
- the final electron energy E’e contains a mass component and a kinetic component (this is just special relativity).
We have in total three unknowns: the final photon energy, the final electron energy and the final electron momentum.
The last bullet above connects the last two of these three unknowns, and the two conservation laws above-mentioned allow to solve the problem entirely.
The solution reads: 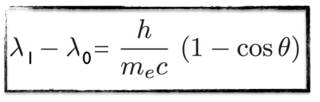
This formula correctly reproduces the observations, which is why it was a success…
SUMMARY - THE PHYSICS BEHIND THE COMPTON EFFECT
What is important in the derivation of the formula above is that two ideas are combined.
We use the fact that light can be treated as a particle, and we employ relations connecting the behavior of this particle to the one of the corresponding wave. In this post, I hence showed what it took to Compton to confirm Einstein idea of the photon being both a particle and a wave.
In my next post, I will change the topic a little bit and detail the Bohr model for the hydrogen atom and why it failed, the correct model being indeed given by quantum mechanics.
REFERENCES AND TOC
All the material in this post (and the other ones of the series) is extracted from the lectures I have given on this topic since half a decade, and from my book that will appear, in French, this September.
For more information on the Compton effect, the wikipedia page is not too bad, with many equations. Many lecture notes can also be found on the web.
Table of contents of this series of posts
I. Introduction
1. Concepts and fundations
2. Interactions and conservation laws
3. Systems of particles
II. The origins of quantum mechanics
1. Fundamental physics at the beginning of the 20th century
2. The mysteries of the atomic spectra
3. The mysteries of the black bodies
4. Quantization of the electromagnetic radiation and the birth of the photons
5. The Compton effect (this post).
