Integral of 1/√e^2x+1 (Trigo Approach)

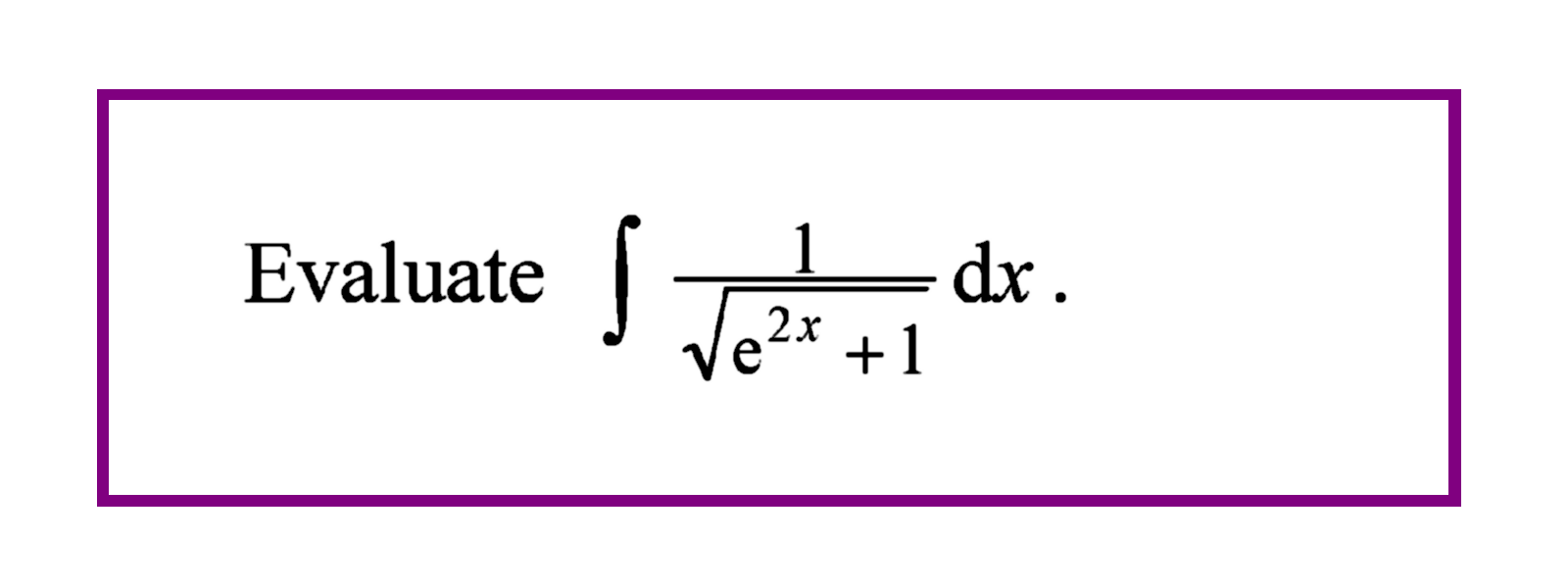
integrateSqrtE2xp -- 00.png

I happened to spot @masterwu's article on the above integral and decided, just for fun, to try doing it via another approach. As he noted, there is another substitution via hyperbolic functions. However, this requires more knowledge that is not so-well known to most students. There is a third type of substitution, that of using a trignometric function which I will demonstrate in this article.

How to do the Trigonometric Substitution

The substitution exploits the trigonometric identity ${\tan^{2}\theta+1=\sec^{2}\theta}$ . Because ${e^{2x}+1}$ looks like ${\tan^{2}\theta+1}$ , I let ${e^x=\tan\theta}$ . See the right half of the working below. To obtain the rule for tranformation of the " ${dx}$ " in the integral, we differentiate the equation with respect to ${\theta}$ . Note that ${\sec^{2}\theta=\frac{1}{\cos^{2}\theta}}$ and that ${e^x=\tan\theta=\frac{\sin\theta}{\cos\theta}}$ . After cancelling and rearranging, we figure out that the " ${dx}$ " will be sort of "replaced" by ${\frac{1}{\sin\theta\cos\theta}d\theta}$ .

integrateSqrtE2xp -- 01.png

${(e^x)^2+1}$ is the same as ${\tan^{2}\theta+1}$ which, as noted earlier, equals to ${\sec^{2}\theta}$ . So the square root expression ${\sqrt{\tan^{2}\theta+1}}$ is the same as ${\sec\theta}$ . Now, since ${\sec\theta=\frac{1}{\cos\theta}}$ , the sec and the cos will cancel. So the whole thing boils down to integrating ${\frac{1}{\sin\theta}}$ i.e. integrating ${\csc\theta}$ . The answer to integrating the cosecant is ${\ln|\csc\theta-\cot\theta|}$ plus the arbitrary constant. For a derivation, you may refer to this web page, or you may verify by differentiating the answer and see if you get back the cosecant function.

integrateSqrtE2xp -- 02.png

Now, since this is an indefinite integral, we must express everything back in terms of x. To help us, we draw a right angled triangle with ${\theta}$ as the angle. Since ${\tan\theta=\frac{opposite}{adjacent}=\frac{e^x}{1}}$ , we label up the opposite side as ${e^x}$ and adjacent side as ${1}$ . The triangle could have been bigger or smaller, but the trigonometric ratios would be the same. Using Pythagoras' Theorem we can figure out the hypothenuse as ${\sqrt{e^{2x}+1}}$ , which bears some uncanny resemblence to the original integrand (expression to be integrated), doesn't it? After completing the right-angled triangle, we can figure out as follows: sine is opposite over hypothenuse, so its reciprocal the cosecant is hypothenuse over opposite, hence ${\csc\theta=\frac{\sqrt{e^{2x}+1}}{e^x}}$ and then the cotangent is the reciprocal of the tangent, and so ${\cot\theta=\frac{1}{e^x}}$ . Noting that ${\frac{\sqrt{e^{2x}+1}}{e^x}}=\sqrt{\frac{e^{2x}+1}{e^{2x}}}}$ and that ${\frac{1}{e^x}=e^{-x}}$ , we simplify to get the final answer at the last line.

Showing equivalence to @masterwu's answer

Are you are wondering: why does my answer look different from @masterwu's answer? Well, actually they are they same. They only appear to be different.

I can demonstrate as follows:-

Since @masterwu's answer has a " ${\frac{1}{2}}$ ", we make " ${\frac{1}{2}\times{2}}$ " appear out of thin air. By the way, we actually do not need to use the modulus if we are sure that the expression in between the two vertical bars is positive. Using the logarithm exponent law ${n\ln{w}=\ln{w^n}}$ , we can fly the 2 up to the top right corner.

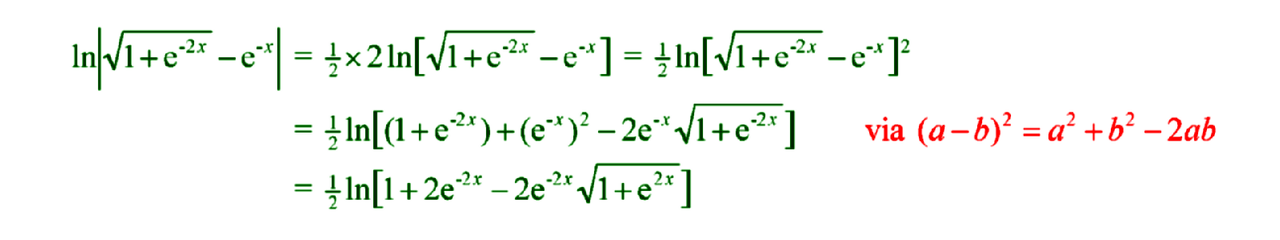
integrateSqrtE2xp -- 03.png

We use the square of differences formula ${(a-b)^2=a^2-2ab+b^2}$ to expand and then simplify to get this last line.

@masterwu's answer can also be simplified further by rationalising the denominator. In the denominator expression, the square root thingy is connected to 1 by a +. If you change that + to a minus, that forms the conjugate expression. Multiply both the numerator and the denominator by ${\sqrt{e^{2x}+1}-1}$ .

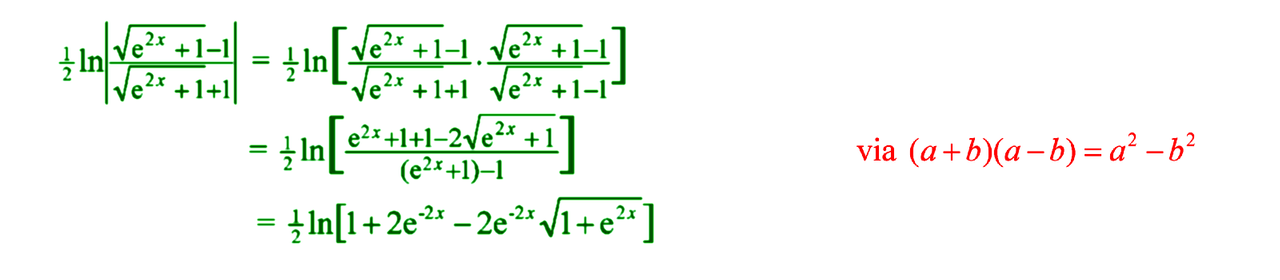
integrateSqrtE2xp -- 04.png

In the next step, we apply the square of differences formula ${(a-b)^2=a^2-2ab+b^2}$ to the numerator and the formula ${(a+b)(a-b)=a^2-b^2}$ to the denominator. After cancelling the 1s, the denominator simplifies to ${e^{2x}}$ and we can simplify the expression to the one shown in the last line. This expression is exactly the same as the previous answer!

So our answers are equal!

Announcements

You might also want to read my recent articles:
Simplifying Roots
"Singapore Math": The Ribbons Problem from PSLE 2017
How to plot vertical lines

If you find my articles useful or interesting, please upvote and resteem them! Thanks !

Cheers!!!

@tradersharpe
-- promoting sharp minds