Hey everyone!
How are you doing today? I sincerely hope all of you are doing well. Life is pretty good right now so I try to make the most of my time and stay productive. This doesn't mean I'm not busy, it just goes to say that I love being busy! I rarely get free time but when I do, I prefer to spend it with loved ones while enjoying nature. Yeah, we know. But that's not the reason I'm uploading this blog. I'm actually back in business with another Engineering blog, so let's do this! Not again...
As promised in my previous posts, which you can easily find by clicking on the links I have provided down below, this is the eighth part of this Introduction to Cartography series. This time I'm taking the chance to share some broad, introductory information regarding Flat Coordinates, which is one of the two main categories of coordinates used by Cartographers. We will also take a deeper look at the various 'Cartesian' (I will elaborate on this) grid systems that are mainly used in the design of map nowadays, so stay focused!
Yep, these are still introductory posts. We will have fun while learning basic, introductory stuff about the art and science of creating 2D depictions of our 3D world with precision. I promise I will do my best to reward your attention with probably failed jokes. Again. It worked in the past. As always, there a high chance of learning a thing or two by reading through this blog, so stay tuned!

Image Source: pixabay.com
In order to be able to define any given point's location with precision, Engineers came up with the idea of creating coordinate systems. These systems would include information regarding topology, which basically refers to any sort of geographic correlations that guarantee the accurate definition of the system's center and axes' orientation, as well as information regarding the metric system and the units of measurement utilized. There are two main categories of coordinate systems that are used nowadays, the first one of which is the oldest one and is known as the Geographical Coordinates System. However, in this blog we will be focusing on the second category, which goes by the name of Flat Coordinates System.
The Flat Coordinates System, which is also called an orthogonal or rectangular coordinate system, is a rather old system as well, regarding at least its basic form that has been used for centuries. This is the perfect type of coordinate system for the precise definition and accurate measurement of the location of geographic entities situated on the surface of a flat projection of the Earth. The Flat Coordinate System in its modern form stems from the Cartesian Coordinate System, which is fair to say given the similarities in geometric attributes and the approach of the system's design in general. Let's share a few words regarding Cartesian Coordinates, which is the system based on which the creation of the Flat Coordinate System was accomplished.
Cartesian Coordinates
The Cartesian Coordinates System is actually a mathematical structure that is mainly comprised of a starting point in 3D space with a known location, and a specific unit of measurement for distances in the metric system utilized in the design of the system. Two axes (Ox, Oy) along the Oxy plane are created in a way that they both intersect the system's known starting point and are vertically oriented towards each other. The Ox and Oy axes are frequently divided into smaller units of measurement that are demonstrated on the projection in a way that serves the purpose of enhancing the observer's ability to extract metric information by looking at the map.
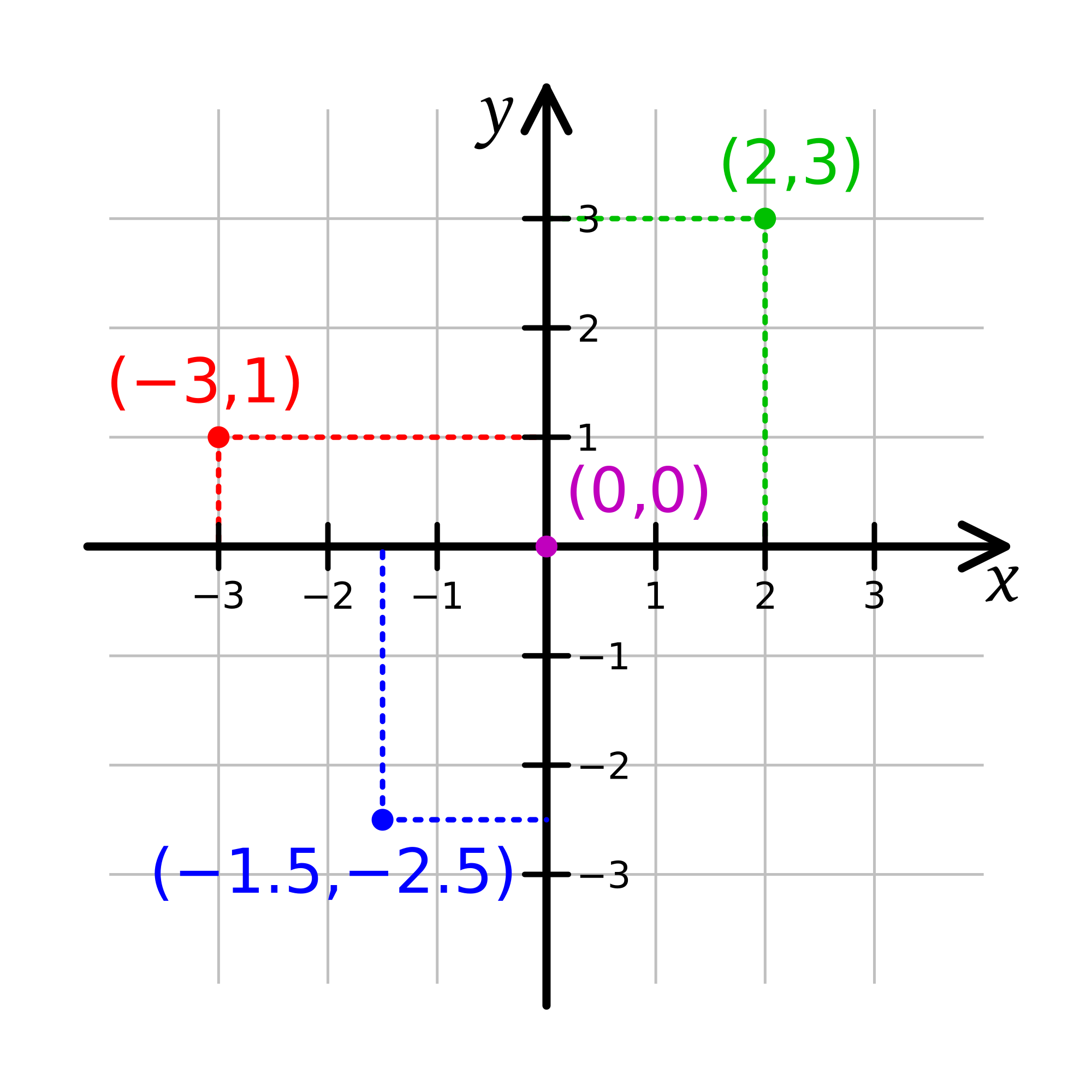
2D Cartesian Coordinate System./ Image Source: commons.wikimedia.org (Public Domain Dedications (Author: Kbolino)
The same sort of spatial distribution analysis reference systems are mainly utilized in the design and construction of graphical representations as well. For instance, magazines or newspapers often provide statistical charts regarding various surveys, so it is safe to say that in these cases it is totally up to the observer to absorb all information available and demonstrated through the use of those graphical elements. Of course the author, who is actually a Cartographer in our case, bares the responsibility of making information available, easy to comprehend and obvious to the eye. Efficient spatial distribution analysis through the design and utilization of the appropriate reference system is the main objective; The Cartesian Coordinates System is what was needed. Cartographers' work globally depends on this system.
Cartographers actually use the Cartesian Coordinate System as a guide and a base for establishing and defining the various coordinate systems utilized in mappings, in order to achieve simplification of all calculations necessary for the conclusion of this process. The differences in the process of calculations between the projection's surface and the reference sphere's surface are trivial in cases of conformal projections, however Cartographers might need to use different coordinate systems according to the level of precision regarding calculations that is demanded. It is worth keeping in mind that the bigger the area of the Natural Terrestrial Surface that is depicted on a projection, the lower the level of precision that can be accomplished. In other words, it is rather significant for Cartographers to possess advanced knowledge regarding the magnitude of precision and distortion included in the various cartographic projections that are mainly used nowadays.
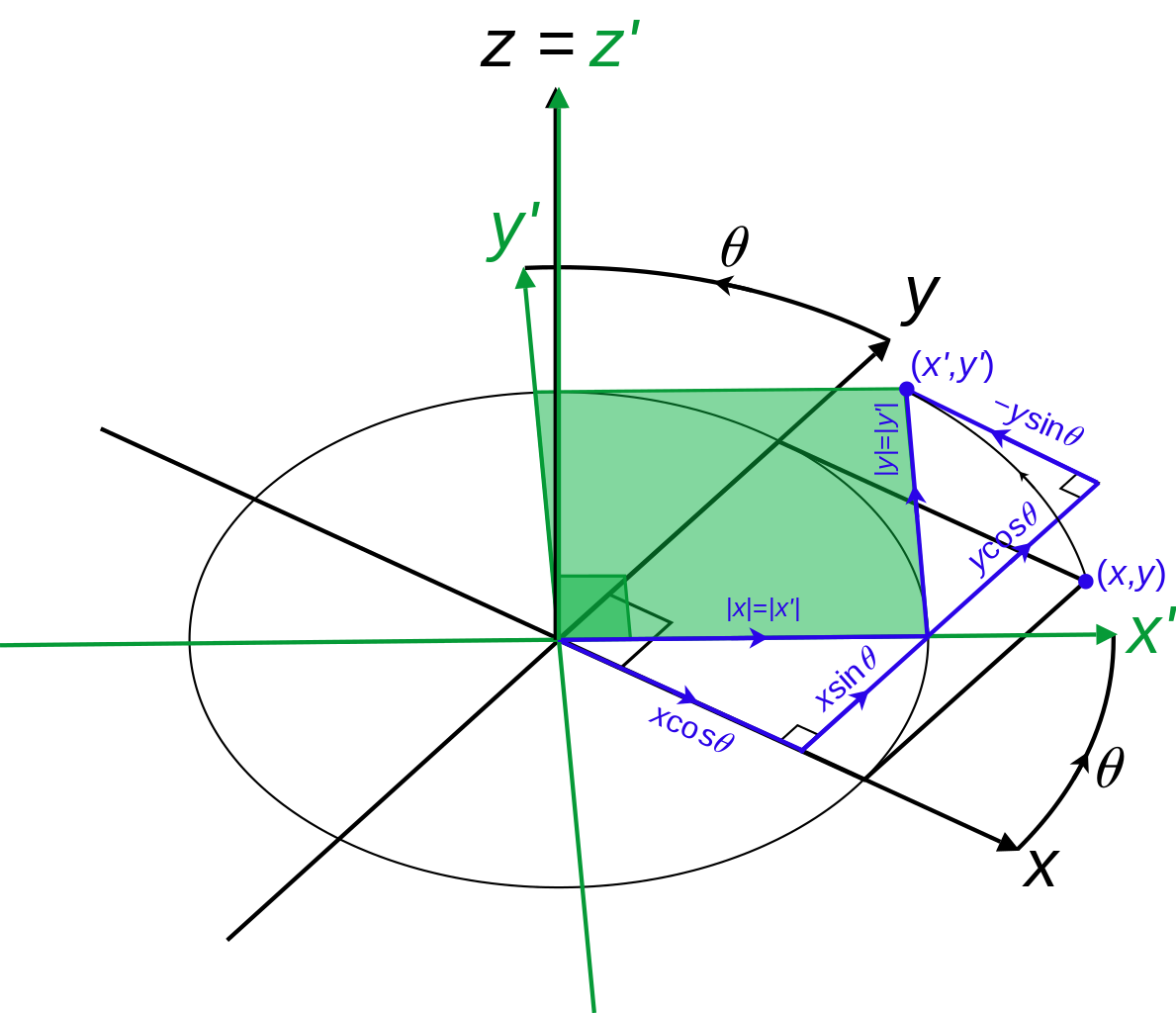
Rotation Transformation of Cartesian Coordinates./ Image Source: commons.wikimedia.org (Creative Commons CC0 1.0 Universal Public Domain Dedication (Author: Maschen)
Flat Coordinates
On a surface of hypothetically infinite area, one cannot spot or establish any sort of reference points without the utilization of a Cartesian Coordinate System. The necessary reference point can be specified and noted as the point at which the primary axes of the system intersect each other. Our system is then established by dividing the Oxy plane into equal-area squares, which is accomplished with the engraving or equidistant, absolutely parallel lines intersecting the axes vertically. Having achieved the creation of the map grid as a result of the process described above, Cartographers are now capable of defining any specific point's coordinates with accuracy in relation to the reference point's given location.
In order to calculate the coordinate values (X,Y), Engineers measure any specific point's distance from both axes, while each measurement refers to the distance from one of the two axes and takes place in the direction that is parallel to the other axis. The coordinate values are then calculated by expressing the measured distances in the grid's units of measurement and taking into consideration the level of accuracy demanded. Horizontal distances are represented by the value of the variable X, whereas vertical distances or variations of location are represented by the value of the variable Y. Taking into consideration how any specific point's location can be described by a pair of numerical values on an orthogonal system's surface, we are capable of calculating the distance between two points as well as the direction of the straight line formed by those two points, as demonstrated below:
D12 = [(X1 - X2)^2 + (Y1 - Y2)2](1/2)
TANa12 = [(Y1 - Y2) / (X1 - X2)]
a12 = arcTAN [(X1-X2) / (Y1-Y2)]
Where 1 and 2 represent any two given points on the Flat Coordinate System's surface and (X1, Y1) & (X2, Y2) their coordinate values. Therefore, D12 represents the distance between those two points and a12 represents the angular address of the straight line formed by those two points, as observed whn moving from point 1 to point 2. The symbol TAN represents a trigonometrical function, thus in order to estimate the value of the angle a12 one must calculate the arcTAN (or TAN^(-1)) in order to define the a12 angle's value. It is a sad truth that the development of all methods described above and the systematic depiction of coordinate systems on the surface of mappings was induced by the technological advancement of weapon systems during WW1. Calculations that included geographical latitude and longtitude values were too complicated to serve the purpose of fast-paced battlefield calculations and therefore, the creation of the Flat Coordinate System served as a practical solution.

3D Cartesian Coordinate System./ Image Source: commons.wikimedia.org (GNU Free Documentation License (Author: Gustavb)
To summarize, in order to define a Flat Coordinates System Engineers have to project the reference sphere on a flat surface by utilizing the appropriate cartographic projection. Then it's time to place tha primary axes Ox and Oy and therefore establish the grid system's reference point where the axes intersect each other. The map's grid system is later constructed by dividing axes into equal parts and engraving absolutely parallel lines which form equal-area squares on the map's surface. Observers are now capable of calculating any given points coordinates by measuring the point's vertical distance from both primary axes. This can be achieved at any level of demanded precision and measured in any metric system used for the calculation of distances on the Natural Terrestrial Surface. And this is probably the most simplified way you will ever find this information published on the web. Kidding, just hope so. :)
Grid Systems
We will now take a deeper look at the main four of the various Cartesian Coordinate Systems broadly used in the USA nowadays and the 'Cartesian' Grid Systems utilized by those. I promised in the introduction that I would elaborate on this and here I am to explain that I just named those grid systems as Cartesian Grid Systems due to the fact that the geometric attributes utilized and demonstrated, as well as the mathematical functions describing their nature and properties are 'taken' from the Cartesian Coordinate System and thus the development of those grids we will talk about was based on this system. That explains why I put it in quotes, I'm just playing around with the meaning of scientific terms as always. There are four main types of Grid Systems used nowadays, as demonstrated below:
- Universal Transverse Mercator Grid System (UTM)
The Universal Transverse Mercator Grid System is broadly used nowadays in cases of topographic mappings and satellite images, as well as in the creation of all sorts of databases in general including informtion regarding various kinds of natural resources and spatial distribution correlations between those. The UTM system is used in cases where high precision regarding topology is demanded and utilizes the meter (m) as a unit of measurement concerning distances. The UTM Grid System is designed and constructed with the utilization of the Tranvserse Mercator Projection. You probably guessed it. It is worth mentioning that it was designed to focus on areas of the Natural Terrestrial Surface situated within the boundaries set by the Parallels of 84N and 80S respectively.
Universal Polar Stereographic Grid System (UPS)
The Universal Polar Stereographic Grid System was designed to focus on areas of the Natural Terrestrial Surface situated North of the Parallel of 84N and South of the Parallel of 80S, providing a coordinate and grid system which can achieve the precision levels of the UTM. The direction of the North on the grid is absolutely parallel to the direction of the central Meridian. It is worth mentioning that the grid zones in the UPS system are divided into equal-area squares, just like in the case of the UTM system. The UPS Grid System is constructed with the utilization of a version of the Stereographic Azimuthal Projection that is centered on the Earth's North Pole. This gives the UPS Grid System the significant attribute of preserving the Scale Factor along the Parallels's direction.State Plane Coordinate System (SPC)
The State Plane Coordinate System was designed and created by the U.S. Coast and Geodetic Survey, which is nowadays known and referred to as the U.S. Chart and Geodetic Survey, back in the 1930s. They basically invented an orthogonal coordinates system for each one of the 50 states in order to help Surveying Engineers with the process of Triangulation, which is a technique used in order to create a system of points with known coordinates that would assist the further study and development of the Natural Terrestrial Surface. The SPC Grid System is based on the Transverse Mercator Projection, however there are cases in which the Lambert Conformal Conical Projection is utilized.Public Land Survey System (PLSS)
The Public Land Survey System was designed in 1785, after Congress passed legislation for the creation of an orthogonal coordinates system that would be broadly used in the creation of mappings regarding the country's monuments and public property. The grid system used in the PLSS bares fundamental differences from the ones used in the UTM and the UPS systems. The primary unit of measurement used in the PLSS regarding surface areas is 1 hectare, which equals 10 000m^2. Today the PLSS covers areas of the Natural Terrestrial Surface that include more than 75% of land situated in the 50 states of America. However calculations are rather complicated due to the fact traditional US units of measurement are utilized. 1 hectare equals 43 560 square feet or 1/640 square miles...
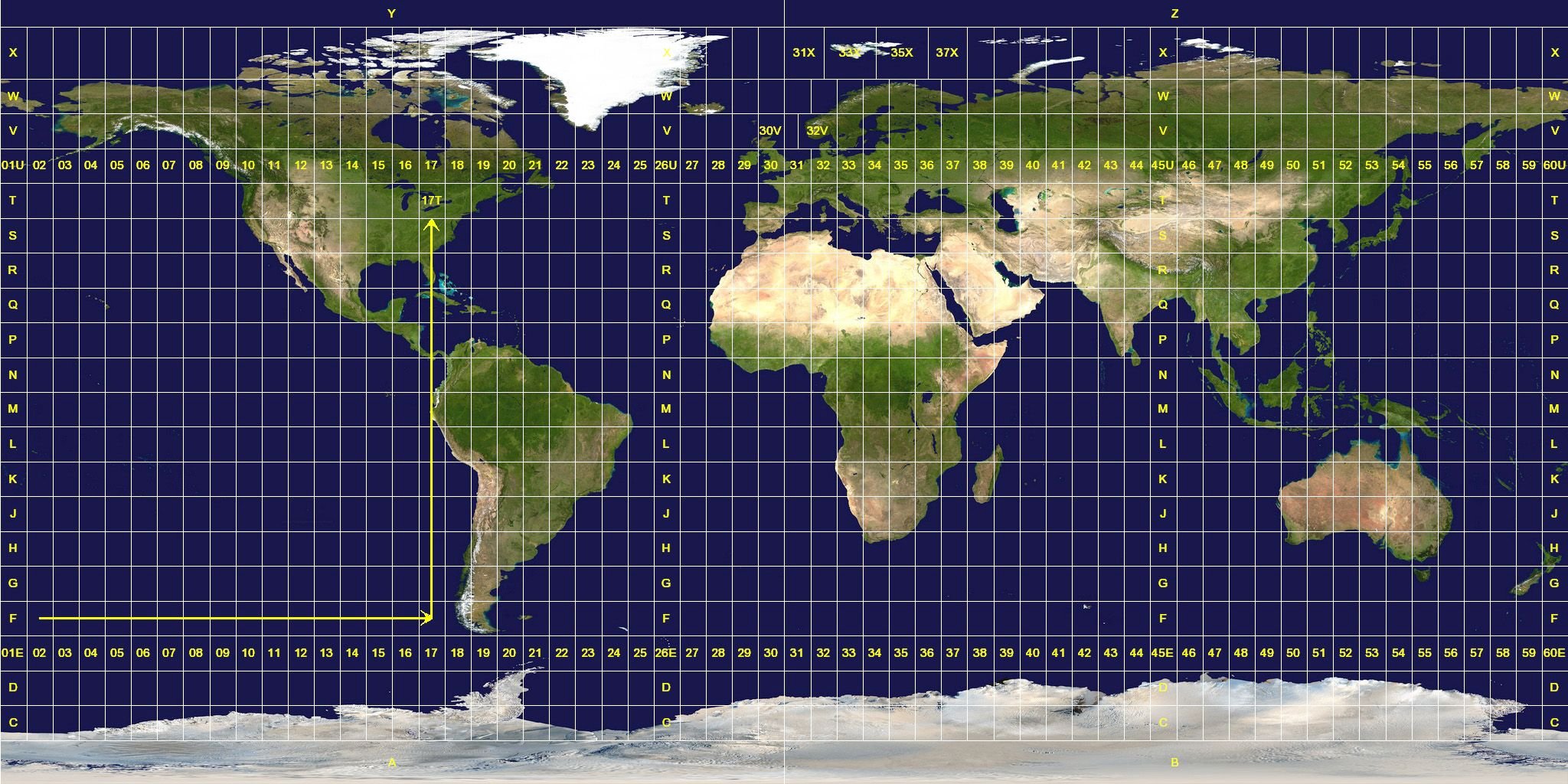
UTM Grid System./ Image Source: commons.wikimedia.org (Public Domain Dedications (Author: NASA Earth Observatory)
Alright, that's it for today guys! Thank you for dropping by my blog and taking the time to read my work. I hope you enoyed this as much as I did. That said, the eighth part of the Introduction to Cartography series, regarding Cartesian Coordinates and Grid Systems has come to an end. Feel free to let me know in the comments below if you do have any questions and I will do my best to provide prompt answers. Follow me for more Engineering blogs! :)
PREVIOUS PARTS OF THE SERIES:

IMAGE SOURCES:
REFERENCES:
University Textbooks & Course Lectures:
Χαρτογραφία Ι/ Cartography I -TSOULOS(National Technical University of Athens, School of Rural & Surveying Engineering, Course Lecture Notes)
Στοιχεία Χαρτογραφίας, Πανεπιστημιακές Εκδόσεις Ε.Μ.Π./Εlements of Cartography, University Publications NTUA -A.H. ROBINSON, J.L. MORRISON, S.C. GUPTILL, A.J. KIMERLING, P.C. MUEHRCKE,(National Technical University of Athens,School of Rural and Surveying Engineering, University Textbook)
Αναλυτική Χαρτογραφία, Πανεπιστημιακές Εκδόσεις Ε.Μ.Π./Analytical Cartography, University Publications NTUA -NAKOS (National Technical University of Athens, School of Rural & Surveying Engineering, University Textbook)
Internet Links:
https://study.com/academy/lesson/the-cartesian-coordinate-system.html
http://www.newworldencyclopedia.org/entry/Cartesian_coordinate_system
https://sectionhiker.com/the-universal-transverse-mercator-utm-grid-system-by-blake-miller/
http://www.nrcan.gc.ca/earth-sciences/geography/topographic-information/maps/9779
https://www.fs.fed.us/r6/icbemp/spatial/fgdc/spatial_reference/ups.html


Thank you for your attention!
Hope you enjoyed this post and did learn a thing or two.
Follow me and stay tuned for more engineering blogs.
Highest Regards
@lordneroo
